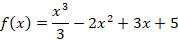Conrad Elber Pinheiro
Professor Guru
Atualizado em 01/08/2023
Crescimento Decrescimento de Funções
Exemplo de crescimento e decrescimento
Teorema - Crescimento e Decrescimento
Ponto Crítico
Estudo da Concavidade de uma Função
Exemplo das concavidades em uma função
Pontos de Inflexão
Análise das concavidades
Exemplo de Crescimento, Decrescimento e Concavidades
Ao final desta página, você pode fazer o download gratuito da apostila sobre Apostila sobre Crescimento, Decrescimento e Concavidades de Funções em formato PDF.
Clique aqui para assistir a playlist com os conteúdos desta página no YouTube
No estudo das derivadas, uma importante aplicação é aquela que se refere ao crescimento e decrescimento de uma função.
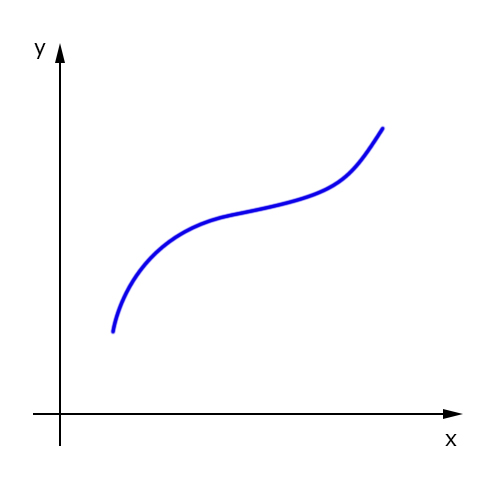
De modo intuitivo, dizemos que uma função é crescente quando o seu gráfico, quando olhado da esquerda para a direita, sempre “sobe”; a função é dita decrescente quando o gráfico, observado da esquerda para a direita, “desce”. Caso nenhuma dessas duas condições ocorra, dizemos que a função é constante e o seu gráfico será horizontal.
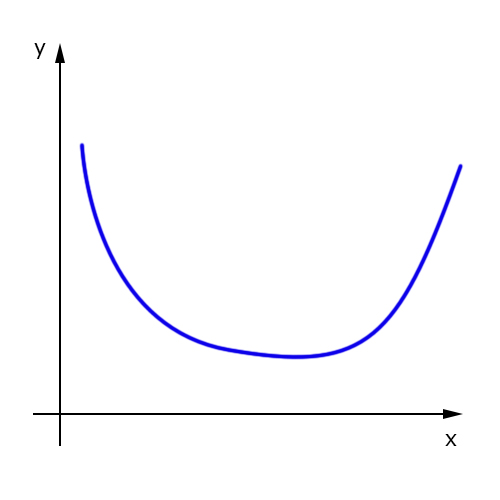
A seguir, veja um exemplo de uma função crescente:
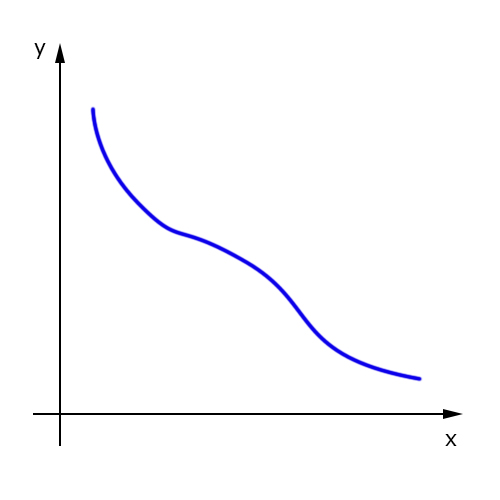
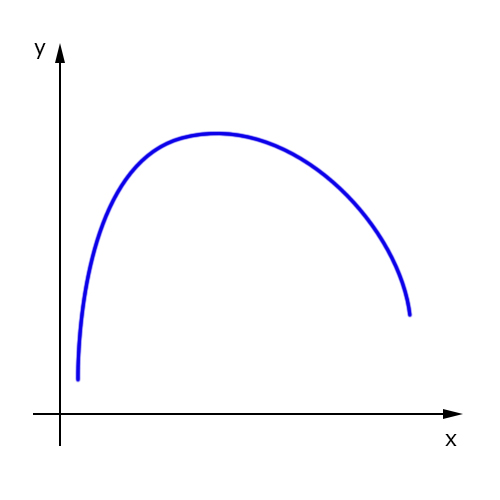
Agora, veja uma função decrescente:
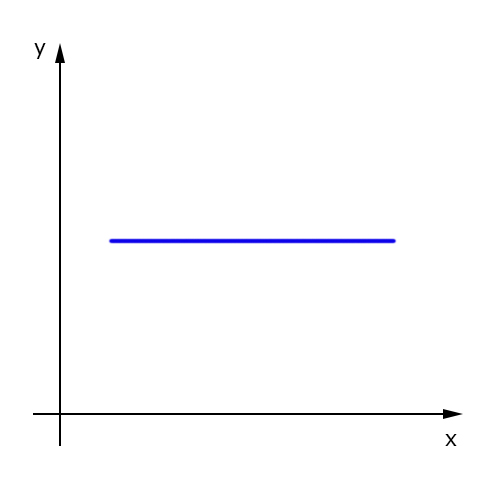
Finalmente, uma função constante:
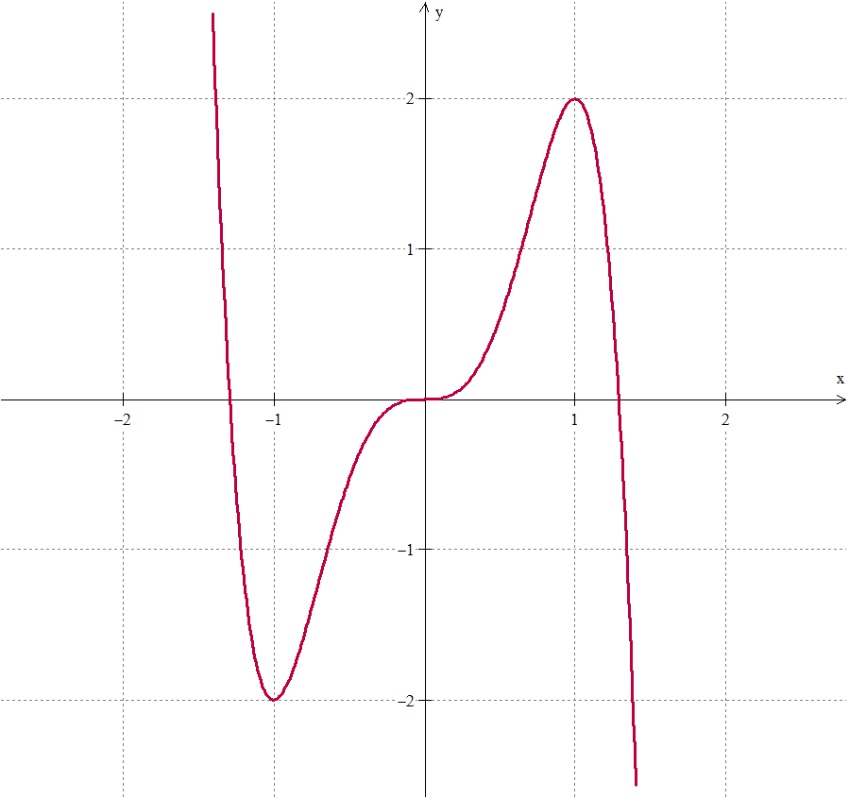
Vejamos o gráfico da função f(x) = -3x⁵ + 5x³ a seguir:
Perceba o comportamento da função ao longo do eixo x:
- em ]-∞;-1[ a função é decrescente;
- em ]-1;1[ a função é crescente;
- em ]1;+∞[ a função é decrescente.
Para sabermos, analiticamente, o comportamento de uma função com relação ao seu crescimento e decrescimento, devemos analisar o comportamento da primeira derivada dessa função.
Seja uma função f, definida no conjunto dos reais, contínua no intervalo ]a,b[ e derivável em todos os pontos desse intervalo. Seja f'(x) a primeira derivada da função f(x):
a) Se f’(x)>0 para todo x pertencente ao intervalo ]a,b[, então a função f será estritamente crescente no intervalo ]a,b[.
b) Se f’(x)<0 para todo x pertencente ao intervalo ]a,b[, então a função f será estritamente decrescente no intervalo ]a,b[.
Para determinarmos os intervalos de crescimento e decrescimento de uma função f(x), nos pontos do domínio em que estiver definida e que satisfizer o teorema anterior, devemos calcular a f’(x) e fazer o estudo do sinal dessa derivada. Aonde o sinal de f’(x) for positivo, a função f(x) é crescente; aonde o sinal de f’(x) for negativo, a função f(x) é decrescente.
Se uma função f possui um ponto de extremo (máximo ou mínimo) local em x=c e a função f é derivável neste ponto, então x=c é um ponto crítico, isto é, f'(c)=0.
Em outras palavras, o ponto crítico pode ser definido como sendo o ponto em que uma função contínua deixa de ser crescente e passa a ser decrescente ou vice-versa.
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
Descrever os intervalos de crescimento e decrescimento da função f(x) = x²+2x-3.
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
Estudar o crescimento e decrescimento da função f(x) = 2x³ – 3x² – 12x + 12.
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
Estudar o crescimento e decrescimento da função f(x) = 1/x.
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
Estudar o crescimento e decrescimento da função f(x) = -x⁴ + x³.
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
Uma função pode apresentar dois tipos de concavidade: para cima ou para baixo.
- Exemplo de uma função com a concavidade para cima:
- Exemplo de uma função com a concavidade para baixo:
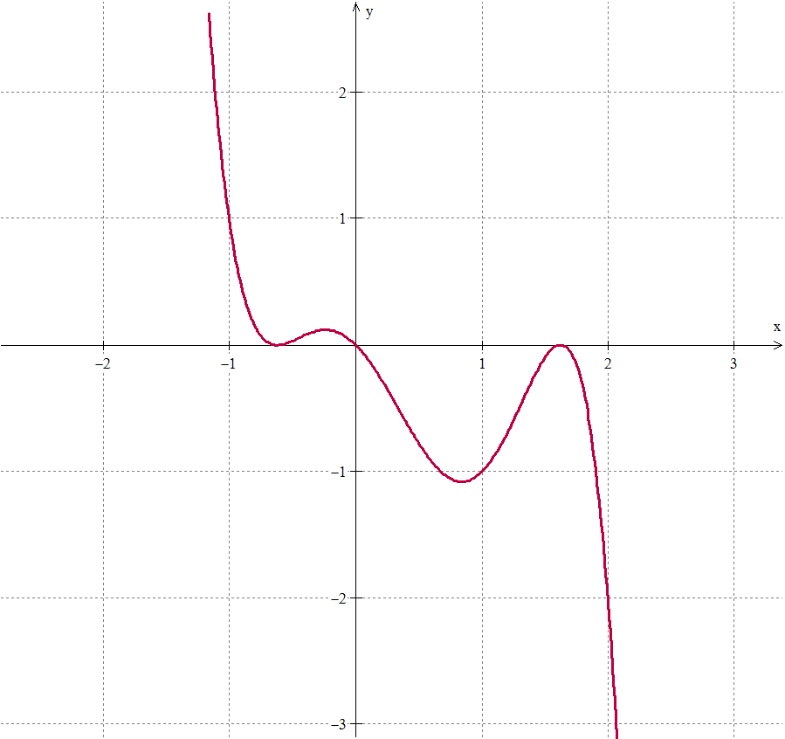
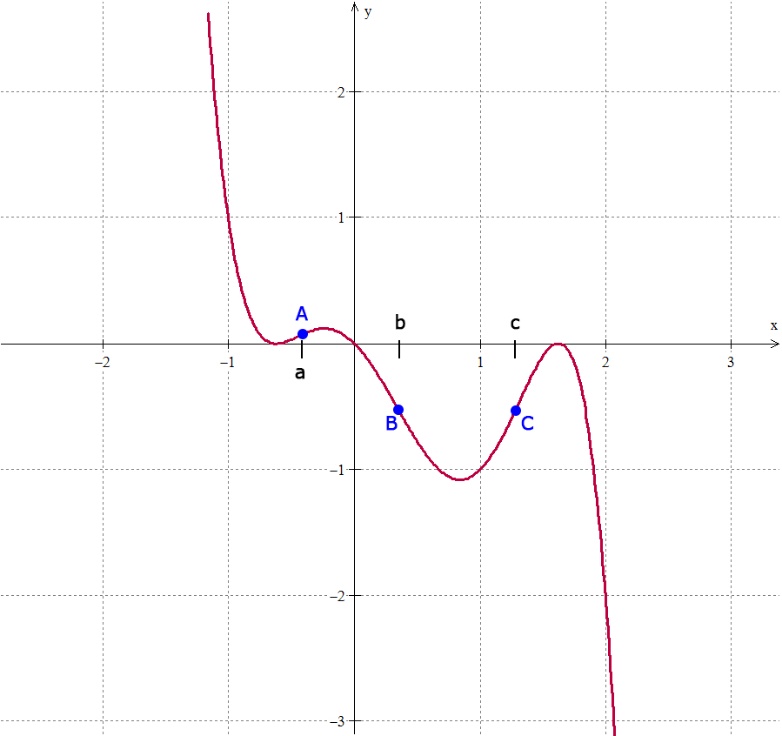
Vejamos o gráfico a seguir que representa a função f(x) = -x⁵ + 2x⁴ + x³ – 2x² – x.
Vamos identificar os pontos em que ocorre a mudança de concavidade:
Para facilitar, vamos considerar alguns valores hipotéticos no eixo x:
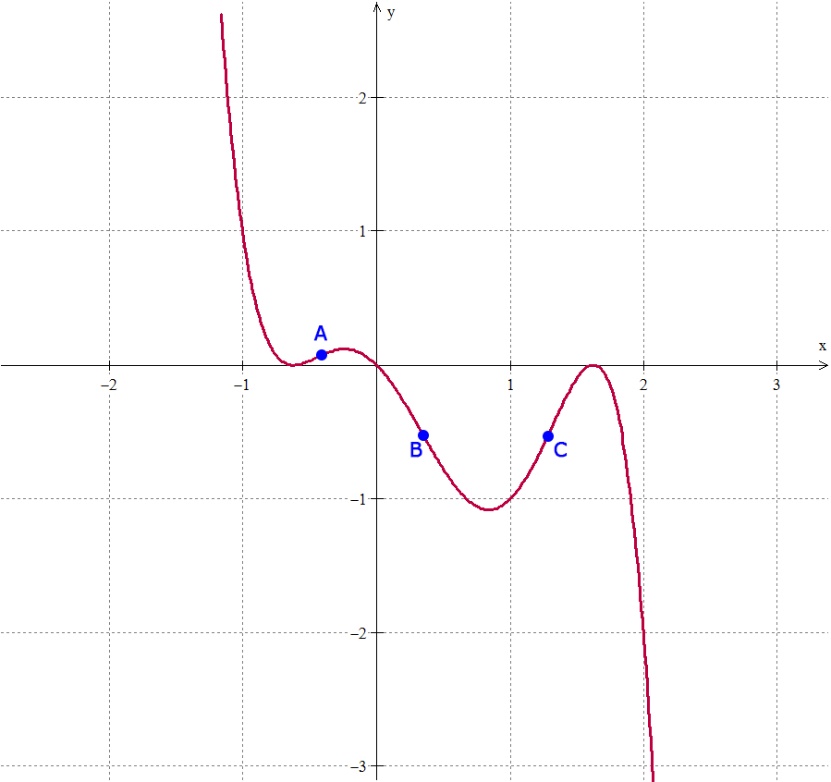
A partir desse gráfico, podemos dizer que a função f possui:
- concavidade para cima no intervalo ]-∞;a[ ;
- concavidade para baixo no intervalo ]a;b[ ;
- concavidade para cima no intervalo ]b;c[ ;
- concavidade para baixo no intervalo ]c;+∞[ .
Note, portanto, que os pontos A, B e C correspondem à mudança de concavidade da função f. Esses pontos são chamados de pontos de inflexão.
São os pontos em que o gráfico de uma função muda a sua concavidade de “para cima” para “para baixo” ou vice versa.
Para analisar a concavidade de uma função, é necessário analisar o comportamento da segunda derivada dessa função.
Seja uma função f, definida no conjunto dos reais, contínua no intervalo ]a,b[ e que admite primeira e segunda derivadas em todos os pontos desse intervalo. Seja f''(x) a segunda derivada da função f(x).
a) Se f’’(x)>0 para todo x pertencente ao intervalo ]a,b[, então a função f terá concavidade para cima no intervalo ]a,b[.
b) Se f’’(x)<0 para todo x pertencente ao intervalo ]a,b[, então a função f terá concavidade para baixo no intervalo ]a,b[.
Para determinarmos as concavidades de uma função f(x), nos pontos do domínio em que estiver definida e que satisfizer o teorema anterior, devemos calcular f’’(x) e fazer o estudo do sinal dessa segunda derivada de f. Aonde o sinal de f’’(x) for positivo, a função f(x) tem concavidade para cima; aonde o sinal de f’’(x) for negativo, a função f(x) tem concavidade para baixo.
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
Fazer o estudo da concavidade da função f(x) = x²+2x-3.
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
Fazer o estudo das concavidades da função f(x) = 2x³ – 3x² – 12x + 12.
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
Fazer o estudo das concavidades da função f(x) = 1/x .
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
Fazer o estudo das concavidades da função f(x) = -x⁴ + x³.
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
Fazer o estudo do crescimento e decrescimento da função f dada a seguir. Depois, fazer o estudo das concavidades.
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
Faça o download gratuito da apostila sobre Crescimento, Decrescimento e Concavidades de Funções em formato PDF.
Baixe AgoraVocê também pode se interessar por:
Lista de exercícios com resolução em vídeo envolvendo problemas de otimização, também conhecido como problemas de máximos e mínimos, através do uso de derivadas
Lista de exercícios com resoluções em vídeos envolvendo cálculo de limites laterais e de limites tendendo a infinito
Lista de exercícios envolvendo limites laterais e infinitos, derivadas elementares, derivadas usando regra do produto e regra do quociente