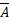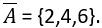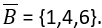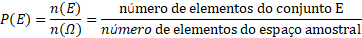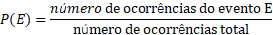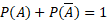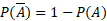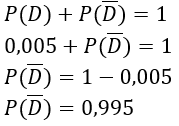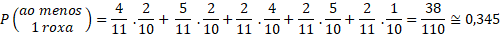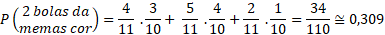Conrad Elber Pinheiro
Professor Guru
Atualizado em 28/07/2023
Introdução
1. Um breve histórico
2. Experimentos aleatórios, espaço amostral e eventos
3. Combinações de eventos
3.1. União de dois eventos
3.2. Interseção de dois eventos
3.3. Eventos mutuamente exclusivos
3.4. Complementar de um evento
4. Probabilidade de um evento
4.1. Probabilidade clássica (ou teórica)
4.2. Probabilidade empírica (ou estatística)
4.3. Probabilidade subjetiva
5. Probabilidade de um evento complementar
6. Probabilidade da união de dois eventos
7. Exercícios resolvidos de probabilidade
8. Espaços equiprováveis e não equiprováveis
9. Independência de dois eventos
9.1. Método da árvore de probabilidades
Lista de Exercícios
Ao final desta página, você pode fazer o download gratuito da apostila sobre Introdução à Probabilidade em formato PDF.
Clique aqui para assistir a playlist com os conteúdos desta página no YouTube
Conscientemente ou inconscientemente, a probabilidade é usada por todos nós na hora de tomar decisões em situações de incerteza. Conhecendo ou não as regras para o seu cálculo, muitas pessoas se interessam por eventos ligados às probabilidades. Do contrário, como poderíamos explicar o grande número de indivíduos que jogam em loterias, bingos, corridas de cavalos, etc.? A utilização das probabilidades indica a existência ou não de um elemento de acaso (incerteza) quanto à ocorrência ou não de um evento. Por exemplo, se lançarmos uma moeda, não podemos afirmar se vamos obter cara ou coroa. A probabilidade indicará uma medida de quão provável é a ocorrência de determinado evento.
São várias as situações em que é desejável ter uma medida (avaliação numérica) de quão provável é a ocorrência de determinado evento futuro: lançamento de um produto, bons lucros em uma operação financeira, chover amanhã de manhã, meu time ganhar o próximo jogo, etc.
A resolução de problemas vinculados a jogos de azar esteve na origem da teoria das probabilidades, que deu seus primeiros passos no século XVI. Os jogadores da época recorriam a matemáticos como Tartaglia e Cardano, solicitando-lhes informações que os favorecessem nos jogos de dados e de baralho.
Foi no século XVII, porém, que a teoria das probabilidades veio adquirir sua forma atual. Os responsáveis por isso foram três franceses: o Cavaleiro de Méré – nobre e jogador inveterado – e Blaise Pascal e Pierre de Fermat, dois matemáticos, que, embora amadores, deram contribuições muito importantes para a Matemática.
Em 1652, o Cavaleiro de Méré propôs a Pascal alguns problemas ligados aos jogos de azar, um dos quais era este: num jogo de azar equilibrado, duas pessoas apostaram 32 moedas de ouro cada uma. Combinou-se que ganharia quem primeiro vencesse 3 partidas; no entanto, o jogo precisou ser interrompido quando uma pessoa tinha vencido 2 partidas e a outra, 1 partida. De que forma devem ser repartidas as 64 moedas de ouro?
Blaise Pascal refletiu nesse problema durante dois anos e, em 1654, passou-o para o jurista Pierre de Fermat. Seguiu-se então uma correspondência entre Pascal e Fermat, que veio constituir-se no ponto de partida da atual teoria das probabilidades.
Pascal e Fermat começaram por concordar que, num jogo interrompido, as moedas deveriam divididas de acordo com as perspectivas de vitórias de cada jogador.
Pascal resolveu o problema analisando o que poderia ocorrer na 4ª partida, para a qual havia 2 possibilidades:
Observemos que, se não houver a 5ª partida, ou a 1ª é a vencedora (e ganha as 64 moedas), ou ambas ficam em igualdades de condições (aí, é justo que cada uma delas fique com 32 moedas). Portanto, ao fim da 4ª partida, a 1ª pessoa já tem garantido 32 moedas, e as 32 restantes têm a mesma possibilidade de ir para uma ou para outra (que essas 32 moedas sejam então divididas em partes iguais pelos dois jogadores).
Com base nesse raciocínio, Pascal conclui que a 1ª pessoa tinha direito a 48 (32 + 16) moedas, e à 2ª cabiam 16 moedas.
Notemos que Pascal resolveu o problema subdividindo-o em casos mais simples, para os quais fossem muito mais óbvias as possibilidades de ocorrer um ou outro fato; em seguida “agrupou” esses casos para chegar à resposta desejada.
Fonte: TROTTA, F. Matemática por assunto 4. s.e. São Paulo: Scipione, 1988.
Entendemos por experimento aleatório os fenômenos que, quando repetidos inúmeras vezes em processos semelhantes, possuem resultados imprevisíveis. O lançamento de um dado e de uma moeda são considerados exemplos de experimentos aleatórios. No caso dos dados podemos ter seis resultados diferentes {1, 2, 3, 4, 5, 6} e no lançamento da moeda, dois {cara, coroa}.
Do mesmo modo, se considerarmos uma urna com 50 bolas numeradas de 1 a 50, ao retirarmos uma bola não saberemos dizer qual o número sorteado. Essas situações envolvem resultados impossíveis de prever. Podemos relacionar esse tipo de experimento com situações cotidianas, por exemplo, não há como prever a vida útil de todos os aparelhos eletrônicos de um lote, pois isso dependerá das condições de uso impostas pelas pessoas que adquirirem o produto. Outro exemplo que demonstra a característica de um experimento aleatório são as previsões do tempo.
Os experimentos aleatórios produzem possíveis resultados que são denominados espaços amostrais. O espaço amostral possui subconjuntos denominados eventos. Como já citado anteriormente, temos que o número possível de elementos no lançamento de um dado é o seu espaço amostral, que geralmente é representado pela letra grega maiúscula ômega (Ω). Ou seja, neste caso temos:
Ω = {1, 2, 3, 4, 5, 6}.
Chamamos de evento a qualquer subconjunto de um espaço amostral. Geralmente os eventos são representados por letras maiúsculas. Podemos definir um evento A da seguinte maneira:
A: sair um número par no lançamento de um dado.
Neste caso, A={2,4,6},
e os subconjuntos, os possíveis eventos são {(1), (2), (3), (4), (5), (6)}. No caso da moeda, o espaço amostral são os dois possíveis resultados {cara e coroa} e os eventos são {(cara), (coroa)}.
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
Uma moeda é lançada 2 vezes. Seja o evento A: sair faces diferentes. Escreva o conjunto que representa o espaço amostral e o evento A.
Vamos definir K como sendo sair cara e C sair coroa. Temos:
Ω = {(K,K), (K,C), (C,K), (C,C)} e
A = {(K,C), (C,K)}.
Perceba que as letras K e C foram colocadas entre parênteses, como se fosse um par ordenado de um plano cartesiano. Isso deve ser feito porque (K,C) é diferente de (C,K). Nessa notação, (K,C) indica a ocorrência de cara no primeiro lançamento e coroa no segundo. Já (C,K) indica coroa no primeiro e cara no segundo.
Nota: se ao invés de lançarmos uma moeda duas vezes lançássemos duas moedas simultaneamente, os conjuntos e A seriam exatamente os mesmos.
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
Neste capítulo estudaremos algumas situações em que podem ocorrer com os eventos: união, intersecção, eventos mutuamente exclusivos e eventos complementares.
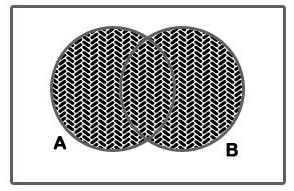
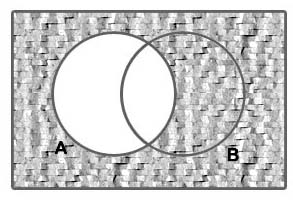
Sejam A e B dois eventos; então A U B corresponde a um evento que ocorrerá quando uma das três condições forem satisfeitas:
- ocorre A e não ocorre B;
- não ocorre A e ocorre B;
- ocorre A e ocorre B simultaneamente.
Graficamente, a região hachurada a seguir representa A U B:
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
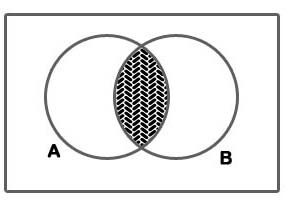
Sejam A e B dois eventos; então A ∩ B será um evento que corresponde à ocorrência de A e B simultaneamente. Dessa forma, podemos perceber que o conjunto A ∩ B é um subconjunto de A U B:
Se A ∩ B = Ø, A e B são chamados mutuamente exclusivos.
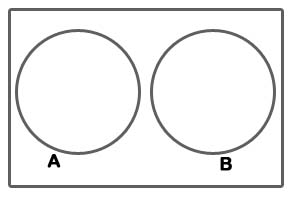
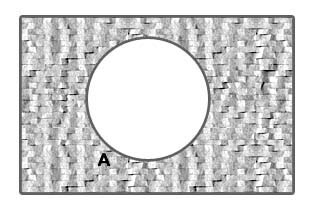
Seja A um evento; então
(lê-se: “A barra”) será também um evento que ocorrerá se, e somente se, A não ocorrer. As figuras abaixo ilustram a situação do complementar em relação a A:
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
Suponhamos o lançamento de um dado. Sejam os eventos:
A: ocorrer um número ímpar;
B: ocorrer um número primo.
Escrever os conjuntos que representam:
a) o espaço amostral;
Ω = {1,2,3,4,5,6}
b) o evento A;
A={1,3,5}
c) o evento B;
Lembre-se que um número primo é aquele que possui exatamente dois divisores: o 1 e ele mesmo. O número 1 possui apenas um divisor, que é o próprio 1. Logo, o número 1 não é primo!
B={2,3,5}
d) o evento ocorrer um número ímpar ou primo;
Esse evento corresponde à união de A com B: A U B = {1,2,3,5}
e) o evento ocorrer um número ímpar e primo;
Esse evento corresponde à intersecção de A com B: A ∩ B = {3,5}
f) o evento não ocorrer um número ímpar;
É o mesmo que obter o conjunto complementar de A:
g) o evento não ocorrer um número primo.
Corresponde ao complementar de B:
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
Existem três tipos de probabilidades: probabilidade clássica, probabilidade empírica e probabilidade subjetiva. A probabilidade de que o evento E ocorrerá é escrita como P(E) e lê-se “probabilidade de um evento E”.
É utilizada quando cada resultado de um espaço amostral é igualmente possível de ocorrer. Ela é calculada pela fórmula:
A probabilidade de ocorrer um evento E é sempre um valor entre 0 e 1, ou seja, entre 0% e 100%:
0 ≤ P(E) ≤ 1
Quando a probabilidade de um evento for 0, isso significa que não há possibilidades desse evento ocorrer. Por isso, dizemos que é um evento impossível. Em contrapartida, se a probabilidade for igual a 1, isto é, a 100%, isso indica que com certeza ocorrerá tal evento. Por isso dizemos que é um evento certo.
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
Lança-se um dado. Sejam os eventos:
A: obter número 5;
B: obter número 1 ou 6;
C: obter número 7;
D: obter um número de 1 a 6.
Calcular a probabilidade de ocorrer cada um dos eventos citados.
Inicialmente, vamos escrever o espaço amostral e os conjuntos que representam cada um dos eventos citados:
Ω = {1,2,3,4,5,6}
A = {5}
B = {1,6}
C = Ø (pois não existe o número 7 no dado)
D = {1,2,3,4,5,6}
Utilizando a definição de probabilidade, temos:
P(A) = 1/6 = 0,1667 ou 16,67%
P(B) = 2/6 = 1/3 = 0,3333 ou 33,33%
P(C) = 0/6 = 0, ou seja, o evento C é chamado de evento impossível.
P(D) = 6/6 = 1 ou 100%, ou seja, o evento D é chamado de evento certo.
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
Quando um experimento (por exemplo, lançar um dado ou lançar uma moeda) é repetido muitas vezes, são formados padrões regulares que permitem encontrar a probabilidade empírica de que determinado evento ocorra.
Por exemplo: ao lançarmos uma moeda 10 vezes, pode ser que ocorra obtermos 2 caras e 8 coroas. Porém, isso não significa que a probabilidade de ocorrer cara não seja 50%. Se repetirmos o experimento lançar uma moeda em torno de 10.000 vezes, é muito provável que o número de caras observadas seja um valor bastante próximo de 5.000.
Esse fato é explicado pela Lei dos Grandes Números: conforme um experimento é repetido várias vezes, a probabilidade empírica de um evento se aproxima da sua probabilidade teórica (real).
A probabilidade empírica de um evento E é a frequência relativa do evento E, ou seja:
Em um Serviço de Atendimento ao Cliente (SAC) de uma empresa, é perguntado sobre o grau de satisfação do cliente com os serviços prestados. Em 1000 atendimentos, 550 consumidores disseram estar “muito satisfeitos”; 300 apenas “satisfeitos”; e o restante, “insatisfeitos”. Qual a probabilidade de a empresa receber a ligação de um cliente “insatisfeito”?
Temos um total de 1000 – 550 – 300 = 150 clientes insatisfeitos. Seja o evento A definido por receber a ligação de um cliente insatisfeito. Assim:
P(A) = 150 / 1000 = 0,15 ou 15%.
Logo, a probabilidade de a empresa receber a ligação de um cliente “insatisfeito” é de 15%.
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
As probabilidades subjetivas resultam da intuição, de suposições fundamentadas e de estimativas.
Por exemplo: um médico “acredita” que a chance de um paciente que possui ferimentos oriundos de um acidente de trânsito sobreviver é 80%. Note que se o mesmo paciente fosse avaliado por outro médico, essa probabilidade poderia ser de, por exemplo, 90%.
Sendo A um evento e "A barra" o evento complementar e o fato de a soma das probabilidades de todos os eventos ser sempre igual a 1, temos:
Ou ainda:
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
A probabilidade de um equipamento sair de fábrica com defeito é de 0,5%. Qual a probabilidade de o equipamento sair funcionando corretamente?
Definindo D: um aparelho apresentar defeito de fábrica, temos que é o evento um aparelho não apresentar defeito de fábrica, ou seja, sair funcionando corretamente.
Lembrando que 0,5% = 0,005, temos:
Logo, a probabilidade é de 99,5%.
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
Segundo os meteorologistas, a probabilidade de fazer um dia ensolarado é 45%; ficar nublado é 30%. Qual a probabilidade de chover? Admita que essas são as únicas possibilidades de ocorrência.
Vamos definir os eventos:
S: o dia será ensolarado;
N: o dia ficará nublado;
C: haverá chuva no dia.
Como a soma de todas as probabilidades é sempre igual a 1, então:
P(S) + P(N) + P(C) = 1
0,45 + 0,30 + P(C) = 1
P(C) = 1 – 0,45 – 0,30
P(C) = 0,25.
Ou seja, a probabilidade de chover é de 25%.
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
Sejam A e B dois eventos tais que A ∩ B = Ø. Neste caso,
P (A U B) = P(A) + P(B) – P(A ∩ B)
É muito comum imaginarmos que a probabilidade de ocorrer A ou B (A U B) seja igual a soma das probabilidades de A com as probabilidades de B. Isso só é válido se estivermos trabalhando com eventos mutuamente exclusivos.
Se A e B são dois eventos tais que (ou seja, são mutuamente exclusivos) então
P (A U B) = P(A) + P(B)
Em muitas situações, podemos utilizar as fórmulas acima para a resolução de um exercício ou calcular a probabilidade diretamente, utilizando a definição.
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
Escolhendo-se aleatoriamente um número natural de 1 a 20, qual é a probabilidade desse número ser múltiplo de 2 ou 3?
Sejam os eventos:
A: o número ser múltiplo de 2;
B: o número ser múltiplo de 3.
Logo, concluímos que:
A U B: o número ser múltiplo de 2 ou 3;
A ∩ B: o número ser múltiplo de 2 e 3.
Os conjuntos são:
A = {2,4,6,8,10,12,14,16,18,20}
B = {3,6,9,12,15,18}
A ∩ B = {6,12,18}
As probabilidades são:
P(A) = 10/20
P(B) = 6/20
P(A ∩ B) = 3/20
Logo,
P(A U B) = 10/20 + 6/20 + 3/20 = 13/20.
Observe que esse valor poderia ser obtido diretamente da definição de probabilidade escrevendo o conjunto:
A U B = {2,3,4,6,8,9,10,12,14,15,16,18,20},
que possui 13 elementos.
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
(FUVEST) A probabilidade de que a população atual de um país seja de 110 milhões ou mais é de 95%. A probabilidade de ser 110 milhões ou menos é de 8%. Calcule a probabilidade de ser 110 milhões.
Vamos definir os eventos:
A: a população tem 110 milhões ou mais;
B: a população tem 110 milhões ou menos.
Logo, podemos concluir que o evento A ∩ B corresponde a população possuir exatamente 110 milhões. E, ainda, A U B corresponde a população ter 110 milhões ou menos ou mais. Portanto, A U B corresponde à todas as possibilidades de tamanho da população. Assim:
P (A U B) = P(A) + P(B) – P(A ∩ B)
1 = 0,95 + 0,08 – P(A ∩ B)
P(A ∩ B) = 0,95 + 0,08 – 1
P(A ∩ B) = 0,03
Logo, a probabilidade de a população ter exatamente 110 milhões vale 3%.
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
Suponhamos o lançamento simultâneo de dois dados. Calcular a probabilidade dos seguintes eventos:
A: ocorrência de números cuja soma seja menor ou igual a 6.
B: ocorrência de números cuja soma seja 8.
C: ocorrência de números cuja soma seja diferente de 8.
D: ocorrência de números iguais nos dois dados ou de números com soma igual a 8.
E: ocorrência de números múltiplos de 3 em pelo menos um dos dados.
Podemos construir o espaço amostral:
Ω = {(1,1), (1,2), (1,3), (1,4), (1,5), (1,6), (2,1), (2,2), (2,3), 2,4), (2,5), (2,6), (3,1), (3,2), (3,3), (3,4), (3,5), (3,6), (4,1), (4,2), (4,3), (4,4), (4,5), (4,6), (5,1), (5,2), (5,3), (5,4), (5,5), (5,6), (6,1), (6,2), (6,3), (6,4), (6,5), (6,6)}
Perceba que nosso espaço amostral possui 36 elementos e que, portanto, poderá ser um pouco mais difícil trabalharmos com a observação direta desse conjunto. Assim, para situações de lançamentos de 2 dados, podemos recorrer a um método prático de resolução que é a construção de uma tabela. Note que as bordas da tabela representam os resultados dos dados e o centro dela corresponde à soma dos resultados:
|
|
1 |
2 |
3 |
4 |
5 |
6 |
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
5 |
6 |
7 |
8 |
9 |
10 |
11 |
|
6 |
7 |
8 |
9 |
10 |
11 |
12 |
Observe que na tabela temos os 36 possíveis resultados do lançamento de dois dados.
Para o cálculo de P(A), basta observamos, na tabela, os resultados cuja soma é menor ou igual a 6. São, ao todo, 15 resultados:
|
|
1 |
2 |
3 |
4 |
5 |
6 |
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
5 |
6 |
7 |
8 |
9 |
10 |
11 |
|
6 |
7 |
8 |
9 |
10 |
11 |
12 |
Logo, P(A) = 15/36 = 5/12.
Com relação ao evento B, observamos facilmente que temos soma igual a 8 em 5 resultados. Portanto P(B) = 5/36.
O evento C é o complementar de B. Logo:
P(C) + P(B) = 1
P(C) = 1 – P(B)
P(C) = 1 - 5/36 = 31/36.
O evento D pede soma igual a 8 ou números iguais nos dois dados. Assim, em nossa tabela, vamos verificar quais são os resultados com soma 8 e aqueles em que os resultados são números idênticos nos dois dados (marcados com X):
|
|
1 |
2 |
3 |
4 |
5 |
6 |
|
1 |
X |
|
|
|
|
|
|
2 |
|
X |
|
|
|
8 |
|
3 |
|
|
X |
|
8 |
|
|
4 |
|
|
|
8 |
|
|
|
5 |
|
|
8 |
|
X |
|
|
6 |
|
8 |
|
|
|
X |
Note que o par (4,4) corresponde a intersecção dos dois eventos. Portanto:
P(D) = 10/36 = 5/18.
Com relação ao evento E, apenas nos interessa os resultados dos dados em si, e não a soma dos resultados. Assim, podemos utilizar uma tabela similar para marcar os resultados que nos interessa. No caso, múltiplos de 3 nos dois dados:
|
|
1 |
2 |
3 |
4 |
5 |
6 |
|
1 |
|
|
X |
|
|
X |
|
2 |
|
|
X |
|
|
X |
|
3 |
X |
X |
X |
X |
X |
X |
|
4 |
|
|
X |
|
|
X |
|
5 |
|
|
X |
|
|
X |
|
6 |
X |
X |
X |
X |
X |
X |
Ao todo, são 20 resultados de interesse. Logo, P(E) = 20/36 = 5/9.
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
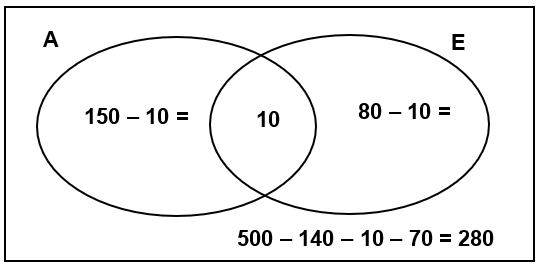
Em um grupo de 500 estudantes, 80 estudam Engenharia, 150 estudam Administração e 10 estudam Engenharia e Administração. Se um aluno é escolhido ao acaso, qual a probabilidade de que:
a) ele estude Administração e Engenharia?
b) ele estude somente Engenharia?
c) ele estude somente Administração?
d) ele não estude Engenharia nem Administração?
e) ele estude Engenharia ou Administração?
Uma forma simples de resolver este tipo de exercício é trabalhar com conjuntos. Lembre-se que devemos iniciar sempre a partir da intersecção.
Agora, podemos responder às questões:
a) P(A ∩ E) = 10/500 = 1/50
b) P(apenas E) = 70/500 = 7/50
c) P(apenas A) = 140/500 = 7/25
d) P(não A e não E) = 280/500 = 14/25
e) P(A U E) = (140+10+70)/500 = 220/500 = 11/25
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
Quando a probabilidade de ocorrência de cada elemento de um espaço amostral for a mesma, dizemos que temos um espaço equiprovável. Porém, se a probabilidade de ocorrência de cada elemento não for a mesma, dizemos que temos um espaço não equiprovável.
Uma urna contém 50 bolas idênticas. Se as bolas forem numeradas de 1 a 50, qual a probabilidade de, em uma extração ao acaso:
a) obtermos a bola de número 27?
Nosso espaço amostral é Ω = { 1, 2, ..., 50} e é equiprovável. Ocorrer a bola 27 significa que o evento possui apenas 1 elemento. Logo:
P(A) = 1/50.
b) obtermos uma bola de número par?
Perceba que existem, de 1 a 50, 25 bolas pares. Ou seja, nosso evento é composto por 25 elementos. Assim:
P(B) = 25/50 = 1/2.
c) obtermos uma bola de número maior que 20?
O evento aqui é C = { 21, 22, ..., 50}, composto por 30 elementos. Logo:
P(C) = 30/50 = 3/5.
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
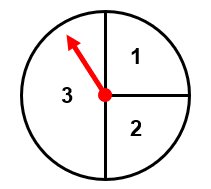
Considere a roleta indicada na figura:
Calcule a probabilidade de ser sorteado cada um dos números mostrados.
Observe que o espaço amostral é Ω = {1, 2, 3}. Porém, é natural percebemos que a chance de ser sorteado o número 3 é maior que de sair o número 1 ou 2. Logo, se trata de um espaço não equiprovável.
Se dividirmos o círculo em 4 partes iguais, percebemos que o número 1 e o número 2 ocupam uma das quatro partes cada um. Já o número 3 ocupa duas das quatro partes. Dessa forma, é fácil concluir que:
P(1) = 1/4
P(2) = 1/4
P(3) = 2/4 = 1/2.
Resumidamente, perceba que a probabilidade de ocorrer cada um dos números é diretamente proporcional à área desses números na roleta.
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
A probabilidade de ocorrer cara no lançamento de uma moeda viciada é 0,62. Qual é a probabilidade de ocorrer coroa?
Embora se trate de mais um caso de espaço não equiprovável, a resolução deste exemplo é praticamente intuitiva. Seja K o evento sair cara e C sair coroa. Então:
P(K) + P(C) = 1
P(C) = 1 – 0,62
P(C) = 0,38 ou 38%
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
Em uma moeda viciada, a probabilidade de ocorrer cara é igual a quatro vezes a probabilidade de ocorrer coroa. Calcule a probabilidade de ocorrer cara em um lançamento dessa moeda.
Usando as mesmas suposições do exemplo anterior temos também que:
P(K) = 4.P(C).
Como P(K) + P(C) = 1, substituindo a expressão anterior temos:
4.P(C) + P(C) = 1
5.P(C) = 1
P(C) = 1/5
Logo, P(K) = 4/5.
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
Três cavalos P, Q e R disputam um páreo, no qual só se premiará o vencedor. Um apostador afirma que a probabilidade de P vencer é o dobro da probabilidade de Q e que Q tem o triplo da probabilidade de ganhar de R. Qual a probabilidade que cada cavalo tem de vencer?
Pelo enunciado temos:
P(P) = 2.P(Q) (I)
P(Q) = 3.P(R) . (II)
Substituindo (II) em (I) temos:
P(P) = 2.3.P(R)
P(P) = 6.P(R). (III)
Sabemos que
P(P) + P(Q) + P(R) = 1. (IV)
Substituindo (II) e (III) em (IV) obtemos:
6.P(R) + 3.P(R) + P(R) = 1
10.P(R) = 1
P(R) = 1/10
Substituindo o resultado em (II) e (III) obtemos:
P(Q) = 3/10
P(P) = 6/10
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
Em um lançamento de um dado viciado, a probabilidade de observarmos um número é proporcional a esse número. Calcule a probabilidade de ocorrer número maior ou igual a 5.
Seja k um número real. A probabilidade de ocorrer uma face é proporcional ao valor dessa face. Então, temos a tabela:
|
face |
probabilidade |
|
1 |
k |
|
2 |
2k |
|
3 |
3k |
|
4 |
4k |
|
5 |
5k |
|
6 |
6k |
|
soma |
21k |
k + 2k + 3k + 4k + 5k + 6k = 1
21k = 1
k = 1/21
As probabilidades de ocorrer face 5 e 6 são, respectivamente, 5/21 e 6/21. Portanto,
P(face maior ou igual a 5) = 5/21 + 6/21 = 11/21
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
Dois eventos são estatisticamente independentes se a ocorrência de um deles não afetar a ocorrência do outro. Por exemplo: ao lançarmos uma moeda honesta e observarmos o resultado, podemos ter obtido uma cara. Se lançarmos novamente, a probabilidade de obtermos outra cara não será alterada em função do resultado obtido na(s) jogada(s) anterior(es), ou seja, a probabilidade continua sendo 50%.
Dessa maneira, se A e B são eventos independentes então
P (A ∩ B) = P(A) . P(B)
Essa regra é válida para n eventos independentes A1, A2, ..., An. Isto é válido desde que todas as combinações entre dois ou mais eventos sejam independentes:
P (A 1 ∩ A 2 ∩ ... ∩ A n ) = P(A 1 ) . P(A 2 ) ... P(A n )
Caso A e B não sejam eventos independentes, dizemos que A e B são dependentes.
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
Uma experiência consiste em lançar, simultaneamente, um dado e duas moedas. Qual a probabilidade de obter a face quatro no dado e duas caras?
Como os eventos são, claramente, independentes, visto que o resultado obtido nas moedas e no dado não são influenciados um pelo outro, temos:
P(K ∩ K ∩ 4) = P(K) . P(K) . P(4) = 1/2 . 1/2 . 1/6 = 1/24
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
Lança-se uma moeda 3 vezes. Calcule a probabilidade dos eventos:
A: ocorrem pelo menos duas caras.
B: ocorrem resultados iguais nos três lançamentos.
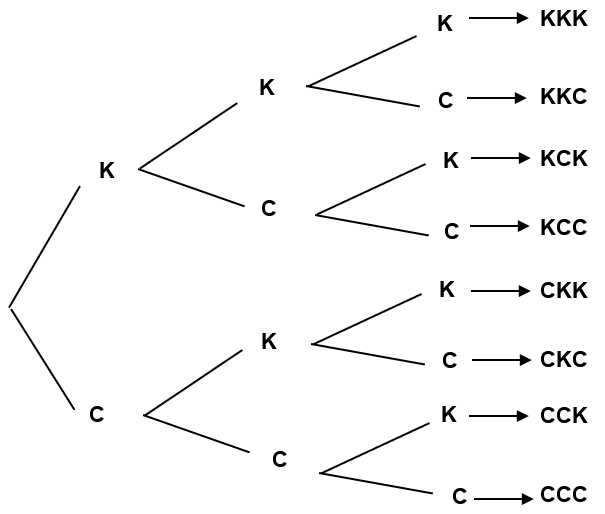
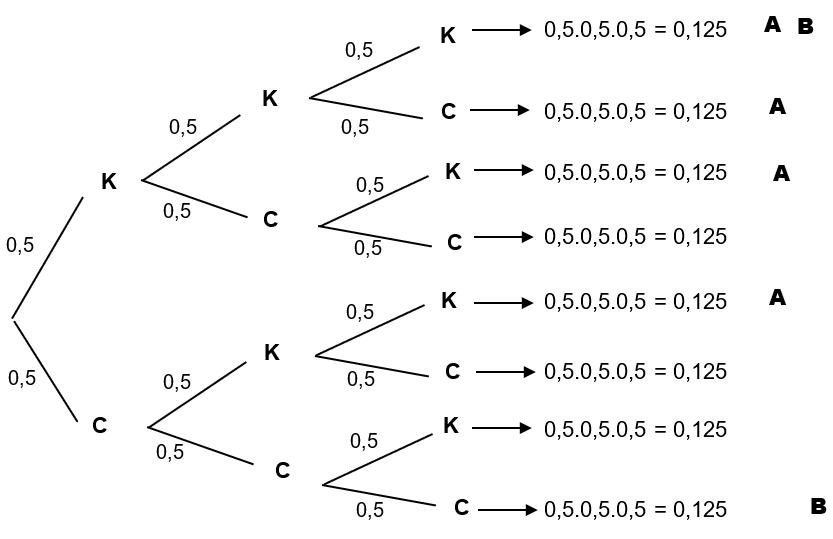
Novamente, estamos trabalhando com eventos independentes. Uma maneira de resolver este exercício, sem a necessidade de se escrever todas as possibilidades do espaço amostral, é trabalhar com o que chamamos de árvore de possibilidades ou árvore de probabilidades. A árvore deve partir de um ponto e “passar”, até o final dela, por todas as possibilidades de resultados. Em seus galhos, anotamos as probabilidades de ocorrências. Ao final dela, multiplicamos os resultados de cada galho para sabermos a probabilidade de um evento em específico.
Inicialmente, vamos montar apenas as possibilidades. Perceba que, partindo do primeiro galho (lado esquerdo da árvore) e fazendo um caminho completo até o final, obtemos todos os 8 elementos do espaço amostral, conforme mostra o lado direito.
Agora, vamos marcar as probabilidades nos galhos. Neste caso, por se tratar de uma moeda honesta, a probabilidade de cara e de coroa são iguais a 0,5.
Indicamos com as letras A e B os casos de interesse, de acordo com os eventos A e B definidos. Para obtermos as probabilidades de cada evento, basta somarmos os resultados indicados na árvore:
P(A) = 4 . 0,125 = 0,5 ou 50% e
P(B) = 2 . 0,125 = 0,25 ou 25%.
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
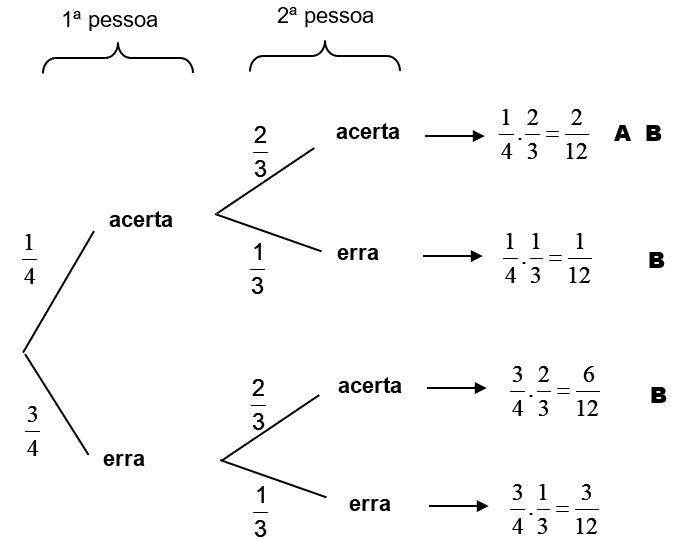
Duas pessoas praticam tiro ao alvo. A probabilidade da 1a atingir o alvo é P(A) = e a probabilidade da 2a atingir o alvo é P(B) = . Admitindo A e B independentes, se as duas derem um tiro ao alvo cada uma, qual a probabilidade de:
a) ambas atingirem o alvo?
b) ao menos uma atingir o alvo?
Vamos resolver, novamente, este exemplo usando a árvore de modo a tornar a resolução por este método prática mais clara. Primeiro, construímos a árvore com as possibilidades, marcando em seguida, nos galhos, as probabilidades de ocorrência. A seguir, calculamos as probabilidades de cada caminho, bastando multiplicar as probabilidades anotadas em cada galho:
As letras ao lado direito indicam os casos de interesse para respondermos aos itens a e b do enunciado. Assim:
a) P(ambas acertarem) = 2/12 = 1/6.
b) P(ao menos uma acertar) = 2/12 + 1/12 + 6/12 = 9/12 = 3/4.
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
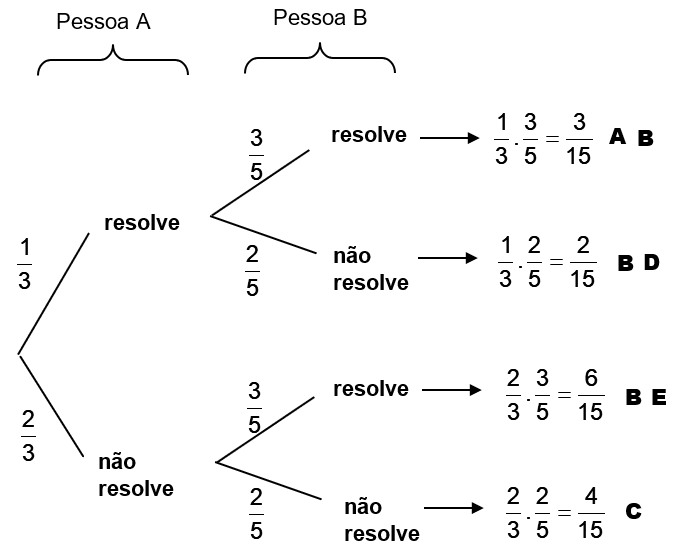
As probabilidades de que duas pessoas A e B resolvam um problema são: P(A) = e P(B) = . Admitindo que as duas pessoas tentem resolver o problema de forma independente, qual a probabilidade de que:
a) ambos resolvam o problema?
b) ao menos um resolva o problema?
c) nenhum resolva o problema?
d) A resolva o problema, mas B não?
e) B resolva o problema, mas A não?
Vamos construir a árvore de probabilidades:
As probabilidades pedidas são:
a) P(ambos resolvam) = 3/15.
b) P(ao menos um resolva) = 3/15 + 2/15 + 6/15.
c) P(nenhum resolva) = 4/15.
d) P(A resolva e B não) = 2/15.
e) P(A não resolva e B resolva) = 6/15.
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
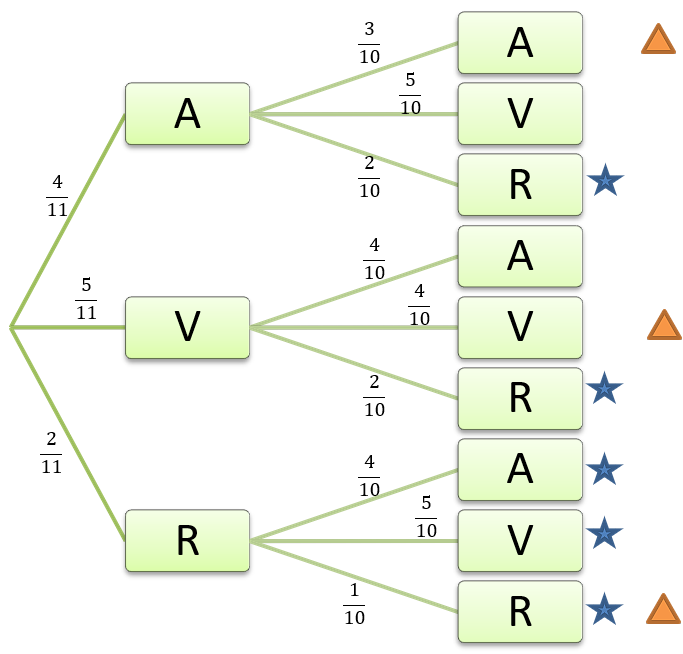
Suponhamos uma urna contendo bolas idênticas sendo: 4 azuis, 5 vermelhas e 2 roxas. São extraídas 2 bolas sem reposição. Calcule a probabilidade de:
a) ser extraída ao menos 1 bola roxa;
b) as duas bolas serem da mesma cor.
Inicialmente, devemos verificar que esta situação trata de um caso de dependência, visto que as bolas são extraídas sem reposição. Ou seja, por exemplo, a probabilidade de retirarmos a 1ª bola e ela ser azul é diferente da probabilidade de a 2ª bola a ser retirada ser azul.
Vamos construir a árvore de probabilidades por etapas. Na primeira retirada, existem 4+5+2 = 11 bolas na urna. Chamemos as cores das bolas de A, V e R para azul, vermelha e roxa, respectivamente. Assim, teremos as seguintes probabilidades:
Na segunda retirada, devemos observar que a 1ª bola não será reposta. Logo, teremos, ao todo, 10 bolas na urna. Se a primeira bola retirada foi a azul, passáramos a ter 3 bolas azuis, 5 vermelhas e 2 roxas dentro da urna. Porém, se a bola retirada foi a vermelha, teremos 4 azuis, 4 vermelhas e 2 roxas. Seguindo essa lógica, podemos escrever as probabilidades para as segundas retiradas:
Para responder ao item a, devemos multiplicar as probabilidades dos galhos da árvore em todos os caminhos indicados com a estrela e somar esses resultados. Assim:
Já para respondermos ao item b, vamos realizar o mesmo procedimento mas com os caminhos indicados com um triângulo:
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
Para acessar a lista de exercícios completa sobre Introdução à Probabilidade, clique no botão abaixo para acessar a página.
IR PARA LISTA DE EXERCÍCIOSFaça o download gratuito da apostila sobre Introdução à Probabilidade em formato PDF.
Baixe AgoraVocê também pode se interessar por:
Fatorial, Princípio Fundamental da Contagem (PFC), Permutação simples, Permutação com repetição, Arranjo e Combinação
Lista de Exercícios sobre: Fatorial, Princípio Fundamental da Contagem (PFC), Permutação simples, Permutação com repetição, Arranjo e Combinação
Noções gerais sobre o que é a Estatística, conceitos de população e amostra, variáveis estatísticas (nominal, ordinal, discreta e contínua), técnicas amostragem, arredondamento de números e lista de exercícios