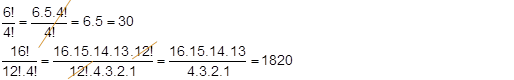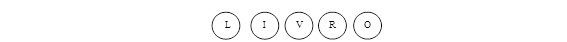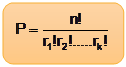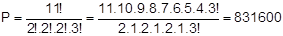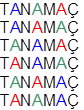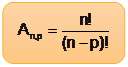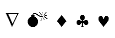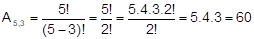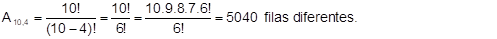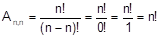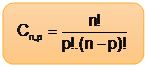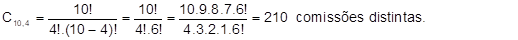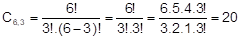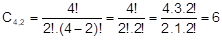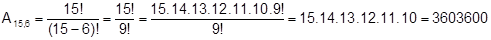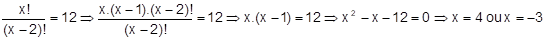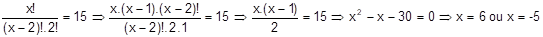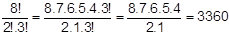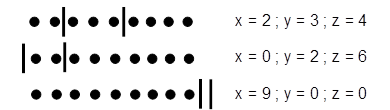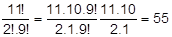Conrad Elber Pinheiro
Professor Guru
Atualizado em 25/07/2023
1. Introdução
2. Fatorial
3. Princípio Fundamental da Contagem (PFC)
4. Permutação sem repetição
Cálculo de Permutação em calculadoras científicas
5. Permutação com repetição
6. Arranjo simples
Cálculo de Arranjo em calculadoras científicas
Observação importante - caso particular de arranjo
7. Combinação
Cálculo de Combinação em calculadoras científicas
8. Exemplos gerais sobre Análise Combinatória
Lista de Exercícios
Ao final desta página, você pode fazer o download gratuito da apostila sobre Análise Combinatória em formato PDF.
Clique aqui para assistir a playlist com os conteúdos desta página no YouTube
A análise combinatória tem por objetivo resolver problemas de contagem. Muitas vezes é complicado realizarmos contagens segundo critérios de ordenação, repetição ou agrupamento; porém, com o auxílio da análise combinatória, esse procedimento torna-se relativamente simples.
O estudo da combinatória é de grande interesse nos mais diversos campos:
• na química estuda-se as possíveis uniões entre átomos;
• o diretor de um colégio faz várias combinações para montar a grade horária de aulas;
• a linguística estuda os possíveis significados de símbolos de uma língua desconhecida;
• a polícia faz combinações na tentativa de decifrar gírias e códigos utilizados por bandidos;
• o DETRAN calcula o número de placas de automóveis disponíveis em determinado Estado;
• o estudo da probabilidade utiliza-se com frequência da combinatória, como será visto mais adiante.
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
Antes de continuarmos no estudo da combinatória, precisamos ver o que é fatorial.
Seja n um número natural com n≥2. Definimos o fatorial do número n pelo símbolo n! tal que
n! = n.(n-1).(n-2). ... .3.2..1
Por definição,
0!=1
1!=1
6! = 6.5.4.3.2.1 = 720
3! = 3.2.1 = 6
A partir da definição, podemos desenvolver técnicas de simplificação de expressões que envolvam fatoriais. Inicialmente, note que
7! = 7.6.(5.4.3.2.1) = 7.6.5!
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
Veja alguns exemplos de simplificação de expressões numéricas envolvendo fatorial:
Inclusive, podemos simplificar expressões algébricas:
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
O Princípio Fundamental da Contagem (PFC) é o caso mais simples da análise combinatória. Consiste em multiplicar o número de possibilidades de cada tipo de ocorrência desde que essas ocorrências ocorram de forma independente. Veja os exemplos a seguir.
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
Vamos começar com um caso bastante simples: uma pessoa tem 3 camisas, 2 calças e 2 cintos diferentes. De quantas maneiras essa pessoa pode se vestir?
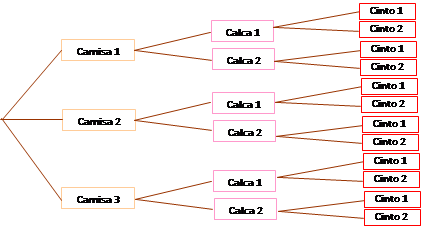
Uma forma de resolver esse problema é utilizando a chamada “árvore de possibilidades”:
Percebemos que há 12 formas dessa pessoa se vestir. Porém, note que tal método seria bastante trabalhoso e demorado caso tivéssemos 10 camisas, 6 calças e 5 cintos, por exemplo.
Precisamos achar um modo mais prático de se obter tal resultado. Observando com cuidado a árvore, percebemos que temos, inicialmente, 3 camisas. Para cada camisa, há 2 possibilidades. Aqui, já temos 2.3 = 6 possibilidades. Porém, para cada uma dessas 6 possibilidades, há mais 2 formas de se vestir, totalizando 6.2=12 maneiras. Em resumo, se um acontecimento ocorre em n situações sucessivas e independentes, sendo que na 1ª situação ocorre de a1 maneiras, a 2ª de a2, ..., a nª de an, então o total de possibilidades é dado por
a 1 . a 2 . ... . a n
Em nosso exemplo, calculamos 3.2.2 = 12. Observação: no caso citado logo após a árvore, em que temos 10 camisas, 6 calças e 5 cintos, teríamos 10.6.5=300 formas diferentes de se vestir.
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
Qual o número de linhas telefônicas móveis (celulares) disponíveis da cidade de São Paulo?
Observação: na época da criação deste exercício, os números dos telefones celulares tinham 8 dígitos e iniciavam com 7, 8 ou 9.
Sabemos que os números de telefones são formados por 8 algarismos e que os celulares começam por 7, 8 ou 9. Assim, esquematicamente, o número de possibilidades para cada algarismo é:
Para o 1° algarismo da esquerda há 3 possibilidades (7, 8 ou 9). Para os 7 algarismos restantes há 10 possibilidades para cada um (0,1,2,...,8,9). Pelo Princípio Fundamental da Contagem, teremos:
3.10.10.10.10.10.10.10 = 3.107 = 30 000 000 = 30 milhões de linhas móveis.
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
Este é o primeiro caso que estamos vendo que trata de métodos de contagem com a utilização de uma fórmula. A compreensão desta situação bem como as seguintes dar-se-á através de exemplos de aplicação.
Suposições:
• não há elementos repetidos;
• a ordem importa;
• todos os elementos são utilizados de uma só vez.
A permutação de n elementos é dada por
P n = n!
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
Se você quiser calcular uma permutação utilizando alguma calculadora científica, verifique se ela possui um botão (ou uma função) geralmente representada por n! ou por x! .
No vídeo a seguir você verá como calcular a permutação usando uma calculadora científica da Casio.
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
Um caso clássico de permutação é aquele que envolve anagramas. Um anagrama é uma sequência de letras que se transpõem e que pode ou não ter sentido. Consideremos a palavra LIVRO. São anagramas dessa palavra:
LIVRO
IVROL
LROVI
OIRVL
.
.
.
Ao todo, quantos anagramas temos? Vamos utilizar o PFC. Imaginemos que temos 5 bolas, cada uma com uma letra:
Temos, também, 5 caixas vazias onde serão colocadas cada uma das bolas (1 bola em cada caixa):
Para a 1ª caixa temos 5 possibilidades (qualquer uma das 5 bolas). Colocada essa bola, restam apenas 4 para a 2ª caixa. Depois, restam 3 bolas para a 3ª caixa e assim por diante.
Pelo PFC teremos 5.4.3.2.1 = 120 anagramas. Isso corresponde exatamente ao caso de permutação de 5 elementos: P5 = 5! = 120. Note que as suposições foram satisfeitas: não há letras repetidas, todas as letras foram utilizadas simultaneamente e a ordem importa, pois LIVRO ≠ IVROL.
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
De quantas maneiras diferentes podemos colocar 4 pessoas para posar, lado a lado, para uma foto?
As suposições sobre a utilização da permutação sem repetição são satisfeitas e teremos, portanto,
P4 = 4! = 4.3.2.1 = 24 fotos possíveis.
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
Suposições:
• a ordem importa;
• temos n elementos dos quais há r1 elementos repetidos do tipo 1, r2 elementos repetidos do tipo 2, ..., rk elementos repetidos do tipo k (k=1,2,3...,n).
Neste caso, o número de permutações é dado por:
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
Qual o número de anagramas da palavra ESTATISTICA (ignorando a acentuação)?
Temos 11 letras das quais 2 são S, 2 são A, 2 são I e 3 são T. Ignoramos a acentuação pois, caso contrário, as letras I e Í seriam diferentes (devido ao acento). O número de anagramas é:
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
Seja a palavra MATANÇA (7 letras, 3 repetidas). Ao todo, teríamos P7 = 7! = 5040 anagramas (supondo a não repetição). Fixemos o anagrama TANAMAÇ. Caso as letras “A” fossem distintas, teríamos, para as demais letras fixadas, P3 = 3! = 6 anagramas:
Porém, tais letras são indistinguíveis. Ou seja, para cada disposição das letras, há 6 anagramas idênticos. Logo, o número de anagramas diferentes da palavra MATANÇA é
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
Suposições:
• não há elementos repetidos;
• a ordem importa.
O arranjo de n elementos tomados p a p é dado por
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
Se você quiser calcular um arranjo utilizando alguma calculadora científica, verifique se ela possui um botão (ou uma função) geralmente representada, geralmente, por nPr.
No vídeo a seguir você verá como calcular o arranjo usando uma calculadora científica da Casio.
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
Uma pessoa dispõe dos símbolos
e quer montar códigos utilizando 3 destes 5 símbolos de modo que não haja repetições de símbolos em cada código. Quantos códigos essa pessoa pode formar?
A ordem dos símbolos importa. Assim, temos um arranjo de 5 elementos tomados de 3 em 3:
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
Numa sala com 10 pessoas, vai-se selecionar aleatoriamente 4 pessoas para se colocar numa fila de atendimento. De quantas maneiras isso pode ser feito?
Novamente, a ordem importa, pois ser o 1° da fila é diferente de ser o último. Assim:
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
Calculemos o arranjo de n elementos tomados n a n (é como se tivéssemos n pessoas numa sala e fossemos selecionar n pessoas – ou seja, todas – para colocá-las numa fila):
Ou seja, A n,n = P n. Logo, a permutação sem repetição é um caso particular de arranjo.
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
Suposições:
• não há elementos repetidos;
• a ordem não importa.
A combinação de n elementos tomados p a p é dada por
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
Se você quiser calcular uma combinação utilizando alguma calculadora científica, verifique se ela possui um botão (ou uma função) geralmente representada, geralmente, por nCr.
No vídeo a seguir você verá como calcular a combinação usando uma calculadora científica da Casio.
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
Seja um grupo de 10 funcionários de uma empresa. Deseja-se formar uma comissão de 4 pessoas. Quantas comissões diferentes podem ser formadas?
Note que a ordem não importa, visto que, escolhendo as pessoas A,B,C e D ou B,D,C e A estamos formando a mesma comissão (o que importa é que as 4 pessoas foram escolhidas e não a ordem com que elas foram escolhidas). Utilizaremos a combinação de 10 elementos tomados 4 a 4:
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
Suponhamos, agora, que tenhamos, dentre os 10 funcionários, 6 homens e 4 mulheres. Queremos formar uma comissão com 3 homens e 2 mulheres. Neste caso, vamos iniciar calculando o número de trios masculinos que podemos formar:
E o número de duplas femininas:
Pelo PFC, teremos 20.6 = 120 comissões. Justificativa do uso do PFC: para cada trio masculino podemos formar comissões com qualquer uma das duplas femininas, ou seja, o trio nº 1 masculino pode-se juntar a uma das 6 duplas femininas; o trio nº 2 masculino pode se juntar a uma das 6 duplas femininas e assim por diante.
Até o momento demos alguns exemplos simples utilizando a análise combinatória com o objetivo de entendermos os usos e diferenças entre os casos de Análise Combinatória. Vale ressaltar que os métodos aqui apresentados não são os únicos existentes. Não trataremos deles aqui, mas é bom que se saiba sobre suas existências: arranjos com repetições, combinações com repetições, permutações circulares, dentre outros.
Agora, daremos alguns exemplos práticos e um pouco mais sofisticados envolvendo os casos de análise combinatória vistos.
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
Em um determinado restaurante, o gerente deseja fazer uma propaganda informando aos consumidores a grande variedade de combinações de pratos que seu cliente poderá fazer. Assim, ele deseja calcular o número de possibilidades sabendo-se que o cliente escolherá uma entrada dentre 8 possíveis, um prato principal dentre 15 diferentes e uma sobremesa dentre 10 disponíveis.
Neste caso, utilizaremos o princípio multiplicativo, visto que cada entrada poderá ser escolhida com qualquer um dos 15 pratos principais que por sua vez, cada um deles, podem acompanhar qualquer uma das 10 sobremesas.
O número total de combinações é: 8 . 15 . 10 = 1200 possibilidades.
Assim, na propaganda, o gerente poderá informar aos seus clientes que o restaurante possui ao todo 1200 refeições diferentes.
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
Suponhamos que as placas de carros com iniciais B, C e D pertençam à cidade de São Paulo (ou seja, ABC 1234 não pertence, por exemplo). Na elaboração de placas, o Detran utiliza-se de todas as letras do alfabeto (incluindo K, Y e W) o que totaliza 26 letras. Suponha, ainda, que nenhuma placa tenha quatro dígitos iguais a zero, ou seja, não existe uma placa do tipo BBC 0000. Pode haver repetição de número e letras. Quantos carros poderão ser emplacados supondo-se a utilização de todas as combinações possíveis em São Paulo?
Utilizaremos, inicialmente, o princípio multiplicativo. A seguir representaremos por quadrados os “lugares” onde podemos colocar as letras e números (os 3 primeiros são letras e os demais, números). O valor dentro dos quadrados indica o total de possibilidades para cada posição.
Note que no primeiro quadrado há 3 possibilidades, visto que estão disponíveis apenas as iniciais B, C e D. Em azul temos os números. São dez possibilidades, pois podemos usar qualquer um dos algarismos de 0 a 9.
Pelo princípio multiplicativo teremos: 3.26.26.10.10.10.10 = 20280000 possibilidades.
Porém, devemos lembrar que não existem placas do tipo # # # 0 0 0 0. Assim, calcularemos o número de placas que levam 4 “zeros”:
Pelo princípio multiplicativo teremos 3.26.26 = 2028 placas desse tipo.
Assim, o número de placas disponibilizados pelo Detran é
20 280 000 – 2028 = 20 277 972 placas.
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
Atualmente é cada vez mais comum o uso de serviços bancários via Internet. Porém, também é cada vez maior o número de hackers que tentam invadir sistemas bancários para desviar dinheiro. Assim, a preocupação com a segurança também aumenta. Além de campanhas preventivas do tipo “jamais divulgue sua senha a um estranho”, “o banco não solicita sua senha por e-mail”, “troque sua senha periodicamente”, alguns bancos tem feitos caríssimos investimentos para melhorar a segurança dos internautas. Uma delas é o aumento do número de dígitos que compõe a “senha eletrônica” quando comparada a “senha do cartão”.
Muitos bancos utilizam para a senha do cartão 4 dígitos numéricos, o que nos daria um total de aproximadamente 10.10.10.10 = 10 000 senhas diferentes. Digo “aproximadamente” pelo fato que muitos bancos não aceitam senhas sequenciais como 2222 ou que contenha data de aniversário ou repetições óbvias do tipo 1212.
Já na Internet, temos bancos que utilizam 8 dígitos numéricos para compor a senha. Neste caso temos 108 = 100 000 000 de combinações diferentes aproximadamente (novamente, devido aos motivos citados). Neste caso, é claro que a segurança é maior, pois são 99 990 000 números a mais. Porém, mais recentemente, outros bancos passaram a se utilizar de 8 caracteres, o que permite incluir letras e números. Considerando, ainda, que o sistema faz uma distinção entre letras maiúsculas e minúsculas teremos um total de, nada mais, nada menos, que
628 = 218 340 105 584 896 218 trilhões de senhas diferentes.
Assim, seria muita, mas muita sorte mesmo, alguém “adivinhar” sua senha ou alguém acessar uma conta bancária de outra pessoa “por engano”.
Como chegamos ao número acima?
Inicialmente pense que você tem 8 quadrados para alojar dentro deles números ou letras (maiúsculas e/ou minúsculas). Dessa forma, teremos, para cada dígito 10 número (de 0 à 9), 26 letras maiúsculas (de A à Z) e outras 26 minúsculas. Como 10+26+26 = 62 então:
Daí usamos, mais uma vez, o princípio multiplicativo obtendo 62⁸ senhas diferentes.
Com tudo isso, será que realmente estamos seguros...?
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
Numa gincana de televisão, o apresentador possui 5 cartelas contendo uma sílaba de uma palavra. O jogador deve adivinhar que palavra é essa conhecendo-se algumas de suas sílabas.
Neste caso, é claro, muitas das possibilidades não serão consideradas pelo jogador devido às regras da gramática portuguesa. Então, o jogador não necessitaria saber todas as combinações possíveis para adivinhar qual a palavra que contém as sílabas:
Neste caso a palavra é ARTESANATO. Fácil, não?
Porém, suponhamos que a palavra apresentada seja desconhecida ou, pelo menos, pouco comum. Por exemplo:
Neste caso, talvez fosse interessante o jogador manipular os cartões colocando-se nas mais diversas ordens até que obtivesse a palavra procurada. Assim, algumas das possibilidades seriam:
CI-DA-GA-NU-DE
DA-NU-GA-CI-DE
DA-CI-GA-DE-NU
NU-DA-CI-GA-DE
DE-NU-GA-CI-DA
E assim por diante. Visto que ele está colocando os cartões em ordens diferentes e cada cartão é diferente do outro e, ainda, a ordem faz diferença, notamos que estamos num caso de permutação.
O número total de combinações que o jogador poderá fazer até achar a palavra é calculado por:
P5 = 5! = 5.4.3.2.1 = 120 anagramas.
Um anagrama é uma ordenação qualquer das letras de uma palavra. Podemos dizer que, neste caso, não seria tão fácil, nem tão rápido, acharmos a palavra desejada.
E você descobriu qual palavra é? A resposta é NUGACIDADE que, segundo o dicionário Aurélio, significa futilidade, nulidade, insignificância.
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
Numa corrida de automóveis, largam 15 carros. Porém, apenas os seis primeiros serão premiados. Diversas pessoas fizeram apostas e ganha aquela que conseguir acertar as 6 primeiras colocações exatamente na ordem de chegada (ou seja, não basta dizer apenas quais foram os seis primeiros, mas é preciso acertar quem foi o primeiro, o segundo e assim por diante).
Neste caso, podemos verificar quantos jogos seriam possíveis fazer, ou melhor, quantos resultados diferentes a corrida poderia ter. Deve estar claro que a ordem de chegada é importante. Como apenas os 6 primeiros são premiados, estamos trabalhando com um caso de arranjo. Assim, temos que escolher 6 pilotos de um total de 15:
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
Quatro carros (c1, c2, c3, c4) disputam uma corrida. Quantas são as possibilidades de chegada para os três primeiros lugares?
Observe que a ordem importa, visto que chegar em primeiro lugar é diferente de chegar em terceiro. Logo, podemos utilizar um caso de arranjo:
A4,3 = 24 “chegadas” diferentes.
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
Os números de telefones fixos de São Paulo (DDD 11) têm 8 algarismos. Determine o número máximo de telefones que podem ser instalados, supondo-se que os números não podem começar com zero nem com um (mas podem começar – por suposição – com qualquer número de 2 a 9).
Vamos utilizar o PFC, visto que os algarismos podem ser repetidos. Note que para o primeiro algarismo só há 8 possibilidades (2, 3, ..., 9). Os demais algarismos podem ser valores de 0 a 9, ou seja, 10 possibilidades:
Pelo PFC temos: 8.10.10.10.10.10.10.10 = 80.000.000 = 80 milhões de telefones.
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
Uma escola possui 18 professores. Entre eles, serão escolhidos: um diretor, um vice-diretor e um coordenador pedagógico, sendo que a mesma pessoa não pode assumir mais de um cargo simultaneamente. Quantas são as possibilidades de escolha?
Novamente, utilizando o PFC temos:
Diretor = 18 possibilidades
Vice-diretor = 17 possibilidades (visto que uma pessoa já foi escolhida para diretor)
Coordenador = 16 possibilidades (pois já escolhemos um diretor e um vice)
Total de possibilidades = 18 . 17 . 16 = 4896.
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
Resolver a equação Ax, 2 = 12.
Utilizando a fórmula de arranjo e os conhecimentos de fatoriais temos:
Como, pela condição de existência devemos ter x ≥ 2, temos que S={4}.
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
Quantos números de 3 algarismos podemos formar com os algarismos 1, 2, 3, 4, 5 e 6, sem repeti-los?
Trabalhando com o PFC, temos as possibilidades:
O total de números é 6.5.4 = 120.
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
Quantos números pares de 4 algarismos podemos formar com os algarismos 0, 1, 2, 3, 4, 5 e 6, sem repeti-los?
Este exemplo é muito similar ao anterior. Porém, aqui, temos que ter cautela com o zero, visto que um número nunca deve ser iniciado com zero. Porém, temos uma segunda restrição, que é o fato de o número ser par e, neste caso, ele deve terminar com 0, 2, 4 ou 6. Percebemos que o zero faz parte de duas restrições (primeiro e último algarismos). Assim, vamos considerar duas situações:
I. o número termina com zero: neste caso, o último algarismo está fixado (zero). Logo, temos 6 possibilidades para o primeiro algarismo (1,2,3,4,5 ou 6). Assim, as possibilidades serão:
Ou seja, teremos 6.5.4.1 = 120 números.
II. o número termina em 2, 4 ou 6 (três possibilidades). O primeiro algarismo não pode ser zero, restando 5 possibilidades. O segundo algarismo pode ser zero, bastando que não seja igual ao primeiro e ao último algarismos definidos. Assim:
O total de número é: 5.5.4.3 = 300.
Logo, o total de número procurado é a soma dos resultados obtidos em I e II, ou seja, 120 + 300 = 420.
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
Resolver a equação Cx, 2 = 15.
Como a condição de existência é x ≥ 2, temos S={6}.
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
Quantas comissões constituídas de 3 pessoas podem ser formadas com 5 pessoas?
Note que a ordem não importa, visto que uma comissão formada pelas pessoas A, B e C ou uma comissão B, C e A representam o mesmo grupo de pessoas. Então, utilizando combinação teremos C5,3 = 10 comissões.
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
Em um ambiente de trabalho há 7 homens e 4 mulheres. Deseja-se formar uma comissão de 5 pessoas sendo que 3 são homens e 2 são mulheres. Quantas comissões podem ser formadas?
Este é uma variação do exemplo anterior. Inicialmente, calculamos o número de comissões possíveis só de homens e só de mulheres:
Homens: C7,3 = 35
Mulheres: C4,2 = 6
Como nossas comissões serão compostas por homens e mulheres, basta multiplicarmos os resultados: 35 . 6 = 210 comissões com cinco pessoas.
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
Temos um grupo de 3 homens e 5 mulheres. Deseja-se formar uma comissão de 4 pessoas sendo que deve haver pelo menos 1 homem presente. Quantas comissões podem ser formadas?
Esta é uma variação do exemplo anterior. Temos que calcular caso a caso a quantidade de homens e mulheres presentes nas comissões:
I. 1 homem e 3 mulheres: C3,1 . C5,3 = 3 . 10 = 30
II. 2 homens e 2 mulheres: C3,2 . C5,2 = 3 . 10 = 30
III. 3 homens e 1 mulheres: C3,3 . C5,1 = 1 . 5 = 5
Como a comissão será do tipo I ou tipo II ou tipo III, devemos somar os resultados obtidos: 30 + 30 + 5 = 65 comissões.
Perceba que não consideramos o caso de 4 homens e 0 mulheres, visto que havia apenas 3 homens no grupo considerado.
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
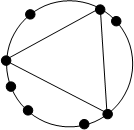
Sobre uma circunferência marcam-se 8 pontos. Quantos triângulos podemos construir utilizando esses pontos?
Para resolver este problema, basta observarmos que a sequência com que escolhemos três pontos quaisquer não importa. Ou seja, escolhidos três pontos, independente da ordem que fizemos a escolha, obteremos o mesmo triângulo. Logo, teremos C8,3 = 56 triângulos possíveis.
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
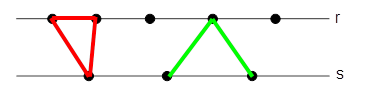
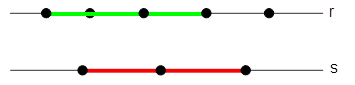
Sobre uma reta r, marcam-se 5 pontos e sobre uma outra reta s, paralela à primeira, marcam-se 3 pontos. Quantos triângulos obteremos unindo 3 quaisquer desses pontos?
É uma variação mais elaborada do exemplo anterior. Podemos utilizar dois métodos distintos para a resolução, que chamaremos aqui de método da inclusão e de método da exclusão.
Neste método, iremos considerar apenas os casos de interesse e, ao final, somamos os resultados para obter o total de triângulos.
Note que temos duas possibilidades para a construção dos triângulos: os que possuem a base na reta r e um vértice na reta s (triângulo da esquerda) ou os que possuem a base na reta s e um vértice na reta r (triângulo da direita).
I. para os triângulos de mesmo tipo que o da esquerda, escolhemos 2 dos 5 vértices para a base e um dos 3 que correspondem ao vértice da reta s: C5,2 . C3,1 = 10 . 3 = 30.
II. para os triângulos de mesmo tipo que o da esquerda, escolhemos 2 dos 3 vértices para a base e um dos 5 que correspondem ao vértice da reta r: C3,2 . C5,1 = 3 . 5 = 15.
Como pode ocorrer o caso I ou o caso II teremos um total de 30 + 15 = 45 triângulos.
Inicialmente, consideramos o número total de triângulos que podemos construir a partir de 5+3=8 pontos:
C8,3 = 56 triângulos.
Porém, pelo fato de termos pontos colineares, devemos calcular quantos “falsos triângulos” computamos, ou seja, quantos “triângulos” formamos utilizando 3 pontos colineares:
I. na reta r temos C5,3 = 10 “falsos triângulos”.
II. na reta s temos C3,3 = 1 “falso triângulo”.
Logo, temos um total de 10+1=11 “falsos triângulos”. Assim, os possíveis triângulos que podemos construir serão 56 – 11 = 45.
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
Qual é o número de anagramas que podemos formar com as letras da palavra INFINITO?
Ao todo são 8 letras, sendo 3 letras “I” e 2 letras “N”. utilizando a fórmula de permutação com repetição, teremos
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
Determine o número de soluções naturais da equação x+y+z=9.
Como estamos trabalhando com o conjunto dos números naturais, cada uma das incógnitas x, y e z podem assumir valores de 0 à 9. Vamos supor que cada bolinha represente uma unidade e que cada barrinha separe os valores de x, y e z da seguinte forma: a quantidade de bolinhas à esquerda da primeira barra corresponde ao valor de x; entre as duas barras correspondem ao valor de y; à direita da segunda barra correspondem ao valor de z. Exemplos:
Dessa forma, vamos traduzir o esquema como se fosse uma palavra com letras repetidas, em que B representa “bolinha” e T representa o “traço”. As figuras anteriores seria, respectivamente, as “palavras” BBTBBBTBBBB, TBBTBBBBBB e BBBBBBBBBTT. Em resumo, o total de soluções corresponde ao número de anagramas de uma das “palavras” anteriores:
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
Em um acampamento há 12 pessoas e 3 barracas. De quantas maneiras podemos organizar essas pessoas de modo que fiquem exatamente 4 pessoas em cada barraca?
Inicialmente, calculamos quantos grupos distintos podemos formar na 1ª barraca: C12,4=495. Para a segunda barraca, devemos escolher 4 pessoas dentre as 8 restantes, visto que 4 pessoas já ocupam a primeira barraca: C8,4=70. Para a última barraca, só resta escolhermos 4 dentre as 4 pessoas que sobraram, o que nos dá, claramente, C4,4=1 grupo possível. Como queremos colocar 4 pessoas na primeira, e na segunda, e na terceira barraca, temos, pelo PFC um total de 495 . 70 . 1 = 34650 formas de organizar o grupo nas barracas.
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
De quantas maneiras podemos arrumar lado a lado 5 livros de Geometria, 4 de Estatística e 3 de Cálculo em uma prateleira de modo que livros de um mesmo assunto fiquem sempre juntos?
Inicialmente, vamos supor uma sequência qualquer das matérias. Por exemplo, Geometria, Estatística e Cálculo. Calculamos de quantas formas podemos organizar os livros de cada matéria separadamente.
Agora, consideramos a ordem com que as disciplinas aparecerão na estante, ou seja, chamando G para geometria, E para Estatística e C para Cálculo temos que a disposição GEC é diferente de CGE, por exemplo. O total de arrumações possíveis é P3 = 3! = 6 para as disciplinas.
Pelo princípio multiplicativo, teremos 120 . 24 . 6 . 6 = 103680 formas de dispor esses livros na prateleira.
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
Para acessar a página contendo a lista de exercícios completa sobre Análise Combinatória, clique no botão abaixo.
IR PARA LISTA DE EXERCÍCIOSFaça o download gratuito da apostila sobre Análise Combinatória em formato PDF.
Baixe AgoraVocê também pode se interessar por:
Noções gerais sobre o que é a Estatística, conceitos de população e amostra, variáveis estatísticas (nominal, ordinal, discreta e contínua), técnicas amostragem, arredondamento de números e lista de exercícios
Gráficos de linhas, colunas, barras, setores (pizza ou torta), gráfico de dispersão, diagrama ramo-e-folhas, pictograma, histograma, polígono de frequências e lista de exercícios
Espaço amostral, eventos, cálculos de probabilidades, probabilidade de um evento complementar, probabilidade da união de dois eventos