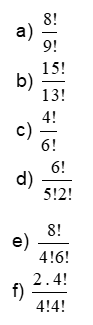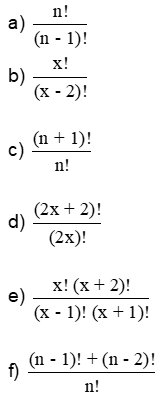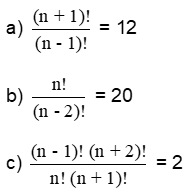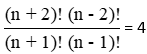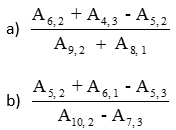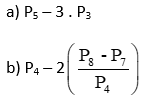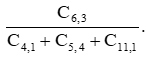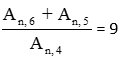Conrad Elber Pinheiro
Professor Guru
Atualizado em 25/07/2023
Para acessar a página contendo a parte teórica com exemplos resolvidos sobre Análise Combinatória, clique no botão.
IR PARA TEORIA E EXEMPLOSAo final desta página, você pode fazer o download gratuito da apostila sobre Análise Combinatória em formato PDF.
Clique aqui para assistir a playlist com os conteúdos desta página no YouTube
1) Calcule o valor dos números fatoriais:
a) 0!
b) 1!
c) 6!
d) 7!
e) 2! + 3!
f) 1! + 4!
g) 3! – 2!
h) 0! + 1!
i) 2!3!
j) 0!5!
2) Simplifique as expressões:
3) Simplifique as frações:
4) Determine o valor de x, de modo que se tenha:
a) x! = 1
b) x! = 24
c) x! = 720
d) x! = x
5) Resolva as equações:
6) (Santa Casa - SP) A solução da equação
é um número natural:
a) par
b) cubo perfeito
c) maior que 10
d) divisível por 5
e) múltiplo de 3
7) (PUC-SP) Se (n – 6)! = 720, então n é igual a:
a) 12 b) 576 c) 16 d) 4 e) 30
8) (UFRN) Se (x + 1)! = 3 (x!), então x é igual a:
a) 1 b) 2 c) 3 d) 4 e) 5
9)
10) (Faap-SP) Num hospital existem 3 portas de entrada que dão para um amplo saguão no qual existem 5 elevadores. Um visitante deve ser dirigir ao 6º andar utilizando-se um dos elevadores. De quantas maneiras diferentes poderá fazê-lo?
11) Uma companhia de móveis tem dez desenhos para mesas e quatro desenhos para cadeiras. Quantos pares de desenhos de mesa e cadeira pode a companhia formar?
12) Quantos números de três algarismos distintos podem ser formados usando-se os algarismos 1, 2, 3, 4 e 5?
13) (FGV-SP) Um restaurante oferece no cardápio 2 saladas distintas, 4 tipos de pratos de carne, 5 variedades de bebidas e 3 sobremesas diferentes. Uma pessoa deseja uma salada, um prato de carne, uma bebida e uma sobremesa. De quantas maneiras a pessoa poderá fazer seu pedido?
14) Quatro times de futebol (Vasco, Atlético, Corinthians e Internacional) disputam um torneio. Quantas são as possibilidades de classificação para os três primeiros lugares?
15) Numa eleição de uma escola há três candidatos a presidente, cinco a vice-presidente, seis a secretário e sete a tesoureiro. Quantos podem ser os resultados da eleição?
16) Determine quantas placas de carro podem ser fabricadas no Brasil.
17) Calcule:
18)
19) Calcule
20) Resolva as equações:
a) Ax, 3 = 4 . Ax, 2
b) An, 2 = 9 . An, 1
c) An, 2 + An – 1, 2 + An – 2, 2 = 20
21) Resolva a equação Cm, 3 – Cm, 2 = 0.
22) Calcule o valor de x na equação Ax, 3 – 6 . Cx, 2 = 0.
23) Efetue a equação:
24) Quantos números de 5 algarismos distintos podem ser formados usando-se os algarismos 1, 2, 3, 5 e 8?
25) Quantos são os anagramas das palavras:
a) CAFÉ
b) BRASIL
26) Quantos números de 3 algarismos distintos podemos formar com os algarismos 1, 2, 3, 4, 5, 6, 7, 8 e 9?
27) Quantos anagramas da palavra EDITORA:
a) começam por A?
b) começam por A e terminam por E?
28) Quantos números de 3 algarismos distintos podemos formar com os algarismos do sistema decimal, sem os repetir, de modo que:
a) comecem com 1.
b) comecem com 2 e terminem com 5.
c) sejam divisíveis por 5.
29) Quantas comissões com 6 membros podemos formar com 10 alunos?
30) Quantos anagramas da palavra PROBLEMA:
a) começam por R?
b) começam por P e terminam por M?
c) começam por vogal?
d) terminam por consoante?
31) De quantas maneiras podemos escalar um time de futebol de salão, dispondo de 8 jogadores?
32) (Faap-SP) Quantos anagramas podem formados com a palavra VESTIBULAR, em que as 3 letras V E S, nesta ordem, permaneçam juntas?
33) Quantas palavras de 2 letras distintas podem ser formadas com as vogais de nosso alfabeto?
34) Quantos números de 4 algarismos distintos podemos formar com os algarismos 0, 1, 2, 3, 4, 5, 6, 7, 8 e 9?
35) Dadas duas retas paralelas, tomam-se 7 pontos sobre uma delas e 4 sobre a outra. Quantos triângulos existem, cujos vértices sejam 3 dos pontos acima considerados?
36) (IME-RJ) Com 10 espécies de frutas, quantos tipos de salada, contendo 6 espécies diferentes, podem ser feitos?
37) Numa sala, temos 5 rapazes e 6 moças. Quantos grupos podemos formar de 2 rapazes e 3 moças?
38) Quantos são os números compreendidos entre 2000 e 3000, formados por algarismos distintos escolhidos entre 1, 2, 3, 4, 5, 6, 7, 8 e 9?
39) Considerando todos os números de seis algarismos distintos que podem ser formados com os algarismos 1, 2, 3, 4, 6, 7 e 9, determine:
a) quantos são pares;
b) quantos são ímpares.
40) De quantas maneiras 5 pessoas podem ser colocadas dentro de um carro, sabendo que:
a) somente 3 sabem dirigir;
b) somente 1 sabe dirigir;
c) todos sabem dirigir.
41) Qual o número de diagonais de um hexágono?
42) (FEI-SP) Calcule o número de diagonais do dodecágono.
43) Determine o número de anagramas formados a partir de:
a) MALA
b) CORRER
c) AMIGA
d) CASSINO
e) RODOVIA
44) Um dado é lançado 4 vezes. De quantos modos distintos pode ser obtida uma sequencia com três faces iguais a 1 e uma face igual a 6?
45) Permutando os algarismos 3, 2, 3, 4, 4 e 5, quantos números de 6 algarismos podemos formar?
46) Uma moeda é lançada 5 vezes. De quantos modos distintos podem ser obtidas 2 caras e 3 coroas?
47) Considere os anagramas formados a partir de CORREDOR. Responda:
a) Quantos são?
b) Quantos começam por R?
c) Quantos começam por COR?
d) Quantos começam e terminam por R?
48) (Unifap-AP) A cidade de Macapá é banhada pelo rio Amazonas e cortada pela linha do Equador. Responda:
a) Quantos são os anagramas da palavra MACAPÁ? (Desconsidere o acento gráfico.)
b) Quantos anagramas da palavra AMAZONAS começam por consoante?
c) Em quantos anagramas da palavra EQUADOR as letras Q, U, A mantêm-se juntas?
49) Determine o número de anagramas formados a partir de:
a) BANANA
b) CACHORRO
c) ASSISTENTE
d) COCADA
e) IRRIGAR
50) (UFBA) Existem 5 ruas ligando os supermercados S1 e S2 e 3 ruas ligando os supermercados S2 e S3. Para ir de S1 a S3, passando por S2, o número de trajetos diferentes que podem ser utilizados é:
a) 15
b) 10
c) 8
d) 5
e) 3
51) (FEI) Obter o número de anagramas formados com as letras da palavra REPÚBLICA nos quais as vogais se mantêm nas respectivas posições.
52) (FUVEST) O número de anagramas da palavra FUVEST que começam e terminam com vogal é:
a) 24
b) 48
c) 96
d) 120
e) 144
53) Júlio deseja pintar a palavra LIVRE em um cartaz de publicidade, usando uma cor em cada letra. De quantos modos isso pode ser feito, se ele dispõe de 8 cores de tinta?
54) Duas pessoas entram num ônibus que tem 7 lugares vagos. De quantas maneiras diferentes 2 pessoas podem ocupar esses lugares?
55) (UFBA) Quatro jogadores saíram de Manaus para um campeonato em Porto Alegre, num carro de 4 lugares. Dividiram o trajeto em 4 partes e aceitaram que cada um dirigiria uma vez. Combinaram também que, toda vez que houvesse mudança de motorista, todos deveriam trocar de lugar. O número de arrumações possíveis dos 4 jogadores durante toda a viagem é:
a) 4
b) 8
c) 12
d) 24
e) 162
56) De quantos modos podem-se arrumar 4 livros de Matemática, 3 de Geografia e 2 de Biologia, numa estante, de modo que:
a) fiquem dispostos em qualquer ordem.
b) os livros de mesmo assunto fiquem juntos.
57) Uma papelaria tem 8 cadernos de cores diferentes, e quero comprar 3 cores diferentes. Quantas possibilidades de escolha eu tenho?
58) Há 12 inscritos em um campeonato de boxe. O número total de lutas que podem ser realizadas entre os inscritos é:
a) 12
b) 24
c) 33
d) 66
e) 132
59) (Cesgranrio-RJ) Um mágico se apresenta em público vestindo calça e paletó de cores diferentes. Para que ele possa se apresentar em 24 sessões com conjuntos diferentes, o número mínimo de peças (número de paletós mais número de calças) de que precisa é:
a) 24
b) 11
c) 12
d) 10
e) 8
60) (FUVEST) Calcule quantos números múltiplos de 3, de 4 algarismos distintos, podem ser formados com 2, 3, 4, 6 e 9.
61) (FGV-SP) Seis pessoas decidem formar 2 comissões com 3 pessoas cada. De quantas formas diferentes isso pode ser feito?
a) 20
b) 120
c) 10
d) 92
e) 48
62) (PUC-SP) Pretende-se formar uma comissão de 5 membros a partir de um grupo de 10 operários e 5 empresários, de modo que nessa comissão haja pelo menos 2 representantes de cada uma das 2 classes. O total de diferentes comissões que podem ser assim formadas é:
a) 1000
b) 185
c) 19400
d) 1750
e) 1650
63) (Santa Casa-SP) Num hospital, há 3 vagas para trabalhar no berçário, 5 no banco de sangue e 2 na radioterapia. Se 6 funcionários se candidatarem para o berçário, 8 para o banco de sangue e 5 para a radioterapia, de quantas formas distintas essas vagas podem ser preenchidas?
a) 30
b) 240
c) 1120
d) 11200
e) 16128000
64) (UNESP) Sobre uma reta marcam-se 3 pontos e sobre outra reta, paralela à primeira, marcam-se 5 pontos. O número de triângulos que obteremos unindo 3 quaisquer desses 8 pontos é:
a) 26
b) 90
c) 25
d) 45
e) 42
65) (FUVEST) Dado um quadrado plano ABCD, escolhem-se 3 pontos sobre o lado AB, 5 pontos sobre BC, 2 pontos sobre CD e 1 ponto sobre AD, de tal modo que nenhum desses pontos coincida com algum vértice do quadrado. Seja x o conjunto dos pontos escolhidos. O número de triângulos com vértice em x é:
a) 165
b) 55
c) 61
d) 154
e) 990
66) (UNICAMP) Num Kombi viajam 9 pessoas, das quais 4 podem dirigir. De quantas maneiras diferentes é possível acomoda-las na Kombi (3 no banco da frente, 3 no banco do meio e 3 no banco de trás), de forma que uma das 4 que dirigem ocupe o lugar da direção?
67) (FUVEST) Seja P o conjunto dos 17 vértices de um heptadecágono regular. Qual o número de triângulos cujos vértice pertencem a P?
68) (FEI) De todos os números menores que 100.000 e maiores que 50.000, quantos são os que lidos da esquerda para a direita ou da direita para a esquerda fornecem o mesmo valor? (Por exemplo: 56365.)
a) 450
b) 1500
c) 1000
d) 900
e) 500
69) (FGV) Considere os algarismos 1, 2, 3, 4, 5 e 6. De quantos modos podemos permuta-los, de modo que os algarismos ímpares fiquem sempre em ordem crescente?
a) 60
b) 120
c) 150
d) 181
e) 240
70) (FCC-BA) Considerem-se todos os anagramas da palavra MORENA. Quantos deles têm vogais juntas?
a) 36
b) 72
c) 120
d) 144
e) 180
71) (Fuvest 2004) Três empresas devem ser contratadas para realizar quatro trabalhos distintos em um condomínio. Cada trabalho será atribuído a uma única empresa e todas elas devem ser contratadas. De quantas maneiras distintas podem ser distribuídos os trabalhos?
a) 12
b) 18
c) 36
d) 72
e) 108
72) (Ueg 2005) A UEG realiza seu Processo Seletivo em dois dias. As oito disciplinas, Língua Portuguesa- Literatura Brasileira, Língua Estrangeira Moderna, Biologia, Matemática, História, Geografia, Química e Física, são distribuídas em duas provas objetivas, com quatro disciplinas por dia. No Processo Seletivo 2005/2, a distribuição é a seguinte:
- primeiro dia: Língua Portuguesa-Literatura Brasileira, Língua Estrangeira Moderna, Biologia e Matemática;
- segundo dia: História, Geografia, Química e Física.
A UEG poderia distribuir as disciplinas para as duas provas objetivas, com quatro por dia, de
a) 1.680 modos diferentes.
b) 256 modos diferentes.
c) 140 modos diferentes.
d) 128 modos diferentes.
e) 70 modos diferentes.
73) (Uel 2006) Na formação de uma Comissão Parlamentar de Inquérito (CPI), cada partido indica um certo número de membros, de acordo com o tamanho de sua representação no Congresso Nacional. Faltam apenas dois partidos para indicar seus membros. O partido A tem 40 deputados e deve indicar 3 membros, enquanto o partido B tem 15 deputados e deve indicar 1 membro. Assinale a alternativa que apresenta o número de possibilidades diferentes para a composição dos membros desses dois partidos nessa CPI.
a) 55
b) (40 - 3) . (15-1)
c) [40!/(37! . 3!)]. 15
d) 40 . 39 . 38 . 15
e) 40! . 37! . 15!
74) (Ufmg 2006) A partir de um grupo de oito pessoas, quer-se formar uma comissão constituída de quatro integrantes. Nesse grupo, incluem-se Gustavo e Danilo, que, sabe-se, não se relacionam um com o outro. Portanto, para evitar problemas, decidiu-se que esses dois, juntos, não deveriam participar da comissão a ser formada.Nessas condições, de quantas maneiras distintas se pode formar essa comissão?
a) 70
b) 35
c) 45
d) 55
75) (Ufv 2004) Um farmacêutico dispõe de 4 tipos de vitaminas e 3 tipos de sais minerais e deseja combinar 3 desses nutrientes para obter um composto químico. O número de compostos que poderão ser preparados usando-se, no máximo, 2 tipos de sais minerais é:
a) 32
b) 28
c) 34
d) 26
e) 30
76) (Cesgranrio 2002) Um brinquedo comum em parques de diversões é o "bicho-da-seda", que consiste em um carro com cinco bancos para duas pessoas cada e que descreve sobre trilhos, em alta velocidade, uma trajetória circular. Suponha que haja cinco adultos, cada um deles acompanhado de uma criança, e que, em cada banco do carro, devam acomodar-se uma criança e o seu responsável. De quantos modos podem as dez pessoas ocupar os cinco bancos?
a) 14 400
b) 3 840
c) 1 680
d) 240
e) 120
77) (Pucmg 2003) Um bufê produz 6 tipos de salgadinhos e 3 tipos de doces para oferecer em festas de aniversário. Se em certa festa devem ser servidos 3 tipos desses salgados e 2 tipos desses doces, o bufê tem x maneiras diferentes de organizar esse serviço. O valor de x é:
a) 180
b) 360
c) 440
d) 720
78) (Uel 2003) Sejam os conjuntos A = {1,2,3} e B = {0,1,2,3,4}. O total de funções injetoras de A para B é:
a) 10
b) 15
c) 60
d) 120
e) 125
79) (Unesp 2003) O conselho administrativo de um sindicato é constituído por doze pessoas, das quais uma é o presidente deste conselho. A diretoria do sindicato tem quatro cargos a serem preenchidos por membros do conselho, sendo que o presidente da diretoria e do conselho não devem ser a mesma pessoa. De quantas maneiras diferentes esta diretoria poderá ser formada?
a) 40.
b) 7920.
c) 10890.
d) 11!.
e) 12!.
80) (Fgv 2005) Um fundo de investimento disponibiliza números inteiros de cotas aos interessados nessa aplicação financeira. No primeiro dia de negociação desse fundo, verifica-se que 5 investidores compraram cotas, e que foi vendido um total de 9 cotas. Em tais condições, o número de maneiras diferentes de alocação das 9 cotas entre os 5 investidores é igual a
a) 56.
b) 70.
c) 86.
d) 120.
e) 126.
81) (FUVEST) Considere todas as trinta e duas sequências, com cinco elementos cada uma, que podem ser formadas com os algarismos 0 e 1. Quantas dessas sequências possuem pelo menos três zeros em posições consecutivas?
a) 3
b) 5
c) 8
d) 12
e) 16
82) (VUNESP) De uma urna contendo 10 bolas coloridas, sendo 4 brancas, 3 pretas, 2 vermelhas e 1 verde, retiram-se, de uma vez, 4 bolas. Quantos são os casos possíveis em que aparecem exatamente uma bola de cada cor?
a) 120
b) 72
c) 24
d) 18
e) 12
83) (MACK) Cada um dos círculos da figura deverá ser pintado com uma única cor, escolhida dentre quatro disponíveis. Sabendo-se que dois círculos consecutivos nunca serão pintados com a mesma cor, então o número de formas de se pintar os círculos é:
a) 100
b) 240
c) 729
d) 2916
e) 5040
84) (UEL) Um professor de Matemática comprou dois livros para premiar dois alunos de uma classe de 42 alunos. Como são dois livros diferentes, de quantos modos distintos pode ocorrer a premiação?
a) 861
b) 1722
c) 1764
d) 3444
e) 242
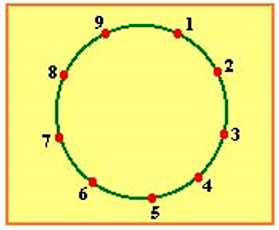
85) Os polígonos de k lados (k múltiplo de 3) que podemos obter com vértices nos 9 pontos da figura, são em número de:
a) 83
b) 84
c) 85
d) 168
e) 169
86) (ITA) O número de soluções inteiras, maiores ou iguais a zero, da equação x+y+z+w = 5 é:
a) 36
b) 48
c) 52
d) 54
e) 56
87) Um salão tem 6 portas. De quantos modos distintos esse salão pode estar aberto?
88) Uma moeda honesta é lançada 8 vezes. Qual a probabilidade de se obter duas coroas consecutivas?
89) (Transpetro-2006) Em um posto de observação foi montado um sinaleiro de formato pentagonal e em cada um de seus vértices foram colocadas duas lâmpadas de cores distintas, escolhidas entre 5 vermelhas e 5 verdes. Convenciona-se que, para a transmissão de uma mensagem, não pode ser acesa mais do que uma lâmpada por vértice, e que o número mínimo de vértices iluminados deve ser três. Se, cada vez que um conjunto de lâmpadas é aceso, transmite-se uma mensagem, o total de mensagens que podem ser transmitidas por esse sinaleiro é
a) 192
b) 128
c) 64
d) 32
e) 16
1. a) 1
b) 1
c) 720
d) 5040
e) 8
f) 25
g) 4
h) 2
i) 12
j) 120
2. a) 1/9
b) 210
c) 1/30
d) 3
e) 7/3
f) 1/12
3. a) n
b) x (x – 1)
c) n + 1
d) (2x + 2) (2x + 1)
e) x (x + 2)
f) 1/(n-1)
4. a) x = 0 ou x = 1
b) x = 4
c) x = 6
d) x = 1 ou x = 2
5. a) n = 3 b) n = 5 c) n = 2
6. A
7. n = 12
8. B
9. m = 4
10. 15
11. 40
12. 60
13. 120
14. 24
15. 630
16. 175 760 000
17. a) b)
18. a) 102 b) -2916
19. 1
20. a) {6} b) {10} c) {4}
21. {5}
22. {5}
23. {7}
24. 120
25. a) 24 b) 720
26. 504
27. a) 720 b) 120
28. a) 72 b) 8 c) 136
29. 210
30. a) 5040 b) 720
c) 15 120 d) 25 200
31. 56
32. 40 320
33. 20
34. 4536
35. 126
36. 210
37. 200
38. 336
39. a) 2160 b) 2880
40. a) 72 b) 24 c) 120
41. 9
42. 54
43. a) 12 b) 120 c) 60
d) 2520 e) 2520
44. 4
45. 180
46. 10
47. a) 3360 b) 1260
c) 60 d) 360
48. a) 120 b) 720
49. a)60 b) 5040
c) 151 200 d) 180 e) 420
50. A
51. 120
52. B
53. 6720
54. 42
55. D
56. a) 9! b) 1728
57. 56
58. D
59. D
60. 72
61. A
62. E
63. D
64. D
65. D
66. 161280
67. 680
68. E
69. B
70. D
71. C
72. E
73. C
74. D
75. C
76. B
77. D
78. C
79. C
80. B
81. C
82. C
83. D
84. B
85. E
86. E
87. 63 modos
88. 65
89. A
Para acessar a página contendo a parte teórica com exemplos resolvidos sobre Análise Combinatória, clique no botão.
IR PARA TEORIA E EXEMPLOSFaça o download gratuito da apostila sobre Análise Combinatória em formato PDF.
Baixe AgoraVocê também pode se interessar por:
Gráficos de linhas, colunas, barras, setores (pizza ou torta), gráfico de dispersão, diagrama ramo-e-folhas, pictograma, histograma, polígono de frequências e lista de exercícios
Espaço amostral, eventos, cálculos de probabilidades, probabilidade de um evento complementar, probabilidade da união de dois eventos
Lista de Exercícios sobre Espaço amostral, eventos, cálculos de probabilidades, probabilidade de um evento complementar, probabilidade da união de dois eventos