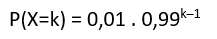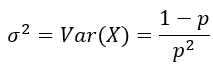1. Distribuição Geométrica

Muitas situações reais podem ser repetidas até atingir–se o sucesso. Um candidato pode prestar uma prova de vestibular até ser aprovado, ou você pode digitar um número de telefone várias vezes até conseguir completar a ligação. Situações como essas podem ser representadas por uma distribuição Geométrica.

Uma distribuição pode ser considerada Geométrica se satisfizer as seguintes condições:

1) Uma tentativa (correspondente a um Ensaio de Bernoulli) é repetida até que o sucesso ocorra, ou seja, ocorrem k–1 fracassos até que ocorra o primeiro sucesso na k–ésima tentativa.

2) As tentativas são independentes umas das outras.

3) A probabilidade de sucesso p é constante em todos os Ensaios de Bernoulli.

Logo, a probabilidade de que ocorra sucesso na tentativa k é dada pela fórmula:

com k=1,2,3,4...

Ou seja, ocorrem k–1 fracassos com probabilidade 1–p até que ocorra um sucesso na tentativa k com probabilidade p.

Assim, podemos aplicar nosso modelo para calcular as probabilidades pedidas:

P(X=1) = 0,01 . 0,99⁰ = 0,01

P(X=2) = 0,01 . 0,99¹ = 0,0099

P(X=5) = 0,01 . 0,99⁴ = 0,0096

P(X=10) = 0,01 . 0,99⁹ = 0,0091

P(X=20) = 0,01 . 0,99¹⁹ = 0,0083

P(X=40) = 0,01 . 0,99³⁹  = 0,0068

Exemplo 2

Por experiência, você sabe que a probabilidade de que você fará uma venda em qualquer telefone dado é 0,23. Encontre a probabilidade de que sua primeira venda ocorra na quarta ou na quinta ligação.

Resolução

X: número da primeira ligação em que ocorre a venda (sucesso).

P(X=4) = 0,23 . 0,77³ = 0,105003

P(X=5) = 0,23 . 0,77⁴ = 0,080852

Logo, a probabilidade desejada é:

P(venda na 4ª ou 5ª ligação) = P(X=4) + P(X=5) = 0,105003 + 0,080852 = 0,186.

Embora um sucesso possa, teoricamente, nunca ocorrer, a distribuição geométrica é uma distribuição de probabilidade discreta porque os valores de x podem ser listados – 1,2,3.... Perceba que conforme x se torna maior, P(X=x) se aproxima de zero. Por exemplo:

P(X=50) = 0,23 . 0,77⁴⁹ = 0,0000006306.

Exemplo 3

Em uma indústria há uma máquina que é inspecionada todos os dias antes de os trabalhos serem iniciados. Por experiências anteriores, sabe-se que a probabilidade dessa máquina estar funcionando corretamente é de 90%. Caso haja algum problema, a produção não é iniciada e a máquina deve passar por uma revisão geral.

a) Qual é a probabilidade de que essa máquina funcione normalmente durante 15 dias e tenha que passar por uma revisão no 16º dia?

b) Qual a probabilidade de levarem pelo menos 5 dias até que aconteça a revisão geral?

c) Em média, a cada quantos dias ocorrerá uma revisão geral?

Resolução

Aqui temos uma distribuição geométrica. Como nosso interesse é de analisar o dia em que ocorrerá a primeira revisão, devemos definir como sendo sucesso o fato de ocorrer essa revisão geral. Sendo assim:

X: número de dias até que ocorra a primeira revisão.

E, portanto, temos que p = 0,10.

a) P(X = 16) = 0,10 . (1 – 0,10)¹⁶⁻¹ = 0,10 . 0,901¹⁵ = 0,0206 ou 2,06%

b) P(X ≥ 5) = 1 – P(X < 5) =

= 1 – [P(X = 1) + P(X = 2) + P(X = 3) + P(X = 4)] =

= 1 – [0,10 . 0,90⁰ + 0,10 . 0,90¹  + 0,10 . 0,90² + 0,10 . 0,90³ + 0,10 . 0,90⁴] =

= 1 – 0,40951 =

= 0,59049 ou 59,049%

c) E(X) = 1/0,1 = 10

Logo, esperamos que as revisões ocorram, em média, a cada 10 dias.  

Exemplo 4

O custo de realização de um experimento é de R$ 1.000,00. Se o experimento falha, um custo adicional de R$ 300,00 tem de ser imposto. Se a probabilidade de sucesso em cada prova é 0,2, se as provas são independentes e continuadas até a ocorrência do primeiro sucesso, qual o custo esperado do experimento?

Resolução

Vamos definir a variável aleatória X como sendo o número de experimentos até ocorrer o primeiro sucesso. Neste caso, p = 0,2. O número esperado de experimentos até a ocorrência do primeiro sucesso é dada por:

E(X) = 1/0,2 = 5 experimentos.

Isso significa que esperamos que ocorram 5 experimentos até que aconteça o primeiro sucesso. Ou seja, nos 4 primeiros ocorrem fracasso e no 5º ocorre sucesso.

O custo para realizar o experimento é de R$ 1000. Ou seja, como serão realizados 5 experimentos, teremos um custo de realização igual a R$ 5000. Porém, nos 4 primeiros experimentos ocorrerá falha, o que implica em um custo adicional de R$ 300 para cada experimento. Logo, teremos um custo adicional total de 4 . 300 = R$ 1200. Dessa forma, o custo total esperado será de 5000 + 1200 = R$ 6.200,00.