Conrad Elber Pinheiro
Professor Guru
Atualizado em 07/07/2023
1. O que é Estatística?
Definição de Estatística
2. Estatística Descritiva e Estatística Indutiva
3.Parâmetros x Estatísticas
4. Planejamento de Experimentos
5.População e Amostra
6. Pesquisa Estatística
6.1. Tipos de amostragem
6.2.Técnicas de Amostragem Não Probabilística
- Amostragem Acidental ou por conveniência
- Amostragem Intencional
- Amostragem por Quotas ou proporcional
- Amostragem Desproporcional
6.3. Técnicas de Amostragem Probabilística
- Amostragem Aleatória simples ou casual simples
Tabelas de Números Aleatórios, Excel e Calculadora Científica
- Amostragem Sistemática
- Amostragem Aleatória Estratificada
- Amostragem por Conglomerado
7. Dado x Variável
7.1. Tipos de Variáveis
7.2. RESUMO
8. Arredondamento de números
8.1. Arredondamentos sucessivos
9. Exercícios
Respostas dos Exercícios
Ao final desta página, você pode fazer o download gratuito da apostila sobre Introdução à Estatística em formato PDF.
Clique aqui para assistir a playlist com os conteúdos desta página no YouTube
Toda pesquisa ou trabalho científico, nas mais variadas áreas, como sociologia, saúde, psicologia, etc., de um modo bem geral, em alguma fase de seu desenvolvimento, se depara com situações que envolvem uma grande quantidade de dados relevantes ao objeto de estudo. Esses dados têm que ser trabalhados e transformados em informações, para que possam ser comparados com outros resultados, ou ainda para julgar sua adequação a alguma teoria. Para isto se recorre a técnicas desenvolvidas com a finalidade de auxiliar a análise dessas informações.
A utilização dessas técnicas, destinadas à análise de situações complexas ou não, tem aumentado e faz parte do nosso cotidiano. Jornais, revistas técnicas artigos, etc., publicam frequentemente tabelas, gráficos, porcentagens e outros dispositivos destinados a complementar a apresentação de um fato ou justificar um argumento.
A ciência que se dedica a esse trabalho é a Estatística.
Estatística: é o conjunto de técnicas que permite, de forma sistemática, coletar, organizar, descrever, analisar e interpretar dados oriundos de estudos ou experimentos, realizados em qualquer área do conhecimento.
No passado, tratar uma grande massa de números era tarefa custosa e cansativa, que exigia horas de trabalho. Recentemente, no entanto, grande quantidade de informações pode ser analisada rapidamente com um computador pessoal e programas adequados. Desta forma, o computador contribui, positivamente, na difusão e uso de métodos estatísticos. Por outro lado, o computador possibilita uma automação que pode levar um indivíduo sem preparo específico a utilizar técnicas inadequadas para resolver um dado problema. Assim, é necessário a compreensão dos conceitos básicos da Estatística, bem como as suposições necessárias para o seu uso de forma criteriosa.
Quando se aborda uma problemática envolvendo métodos estatísticos, deve-se planejar a experiência que nos vai permitir recolher os dados, de modo que, posteriormente, se possa extrair o máximo de informações relevantes para o problema em estudo, ou seja, para a população de onde os dados provêm. Quando de posse dos dados, procura-se agrupá-los e reduzi-los sob forma de amostra.
Seguidamente o objetivo do estudo estatístico pode ser o de estimar uma quantidade ou testar uma hipótese. Utilizamos então técnicas estatísticas convenientes que vão permitir tirar conclusões acerca da população, baseando-se numa pequena amostra, dando-nos ainda uma medida do erro cometido.
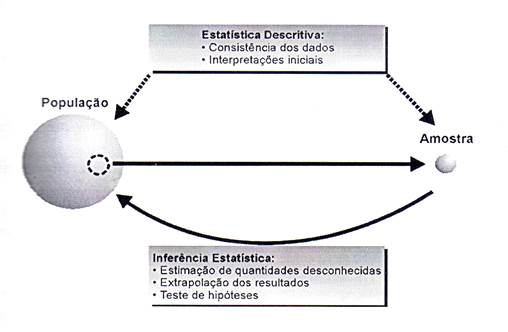
Em uma análise estatística distinguem-se essencialmente duas etapas:
Procura-se descrever e resumir dados, afim de que se possam tirar conclusões a respeito das características de interesse.
Exemplos de características de interesse: idade, sexo, peso.
Exemplos de técnicas descritivas: gráficos, tabelas de frequência, parâmetros associados às frequências, tais como médias, variâncias, etc.
Conhecidas certas propriedades (obtidas a partir de uma análise descritiva de uma amostra), expressas por meio de proposições, imaginam-se proposições mais gerais (extrapolação), que exprimam conclusões para toda a população.
Essas duas etapas estão intimamente relacionadas aos conceitos de População e Amostra, que veremos mais adiante.
• Parâmetros: são medidas populacionais quando se investiga a população em sua totalidade, neste caso é impossível fazer inferências, pois toda a população foi investigada.
• Estatísticas ou Estimadores: são medidas obtidas da amostra, torna-se possível neste caso utilizarmos inferências para que possamos fazer conclusões sobre a população.
Os estudos que utilizam métodos estatísticos vão desde os que são concebidos e executados, dando resultados confiáveis, aos que são concebidos deficientemente e mal executados, levando a conclusões enganosas e sem qualquer valor real. Eis alguns pontos importantes para o planejamento de um estudo capaz de produzir resultados válidos:
Identificar com precisão a questão a ser respondida e definir com clareza a população de interesse.
Estabelecer um plano para coleta de dados. Esse plano deve descrever detalhadamente a realização de um estudo observacional ou de experimento e deve ser elaborado cuidadosamente, de modo que os dados coletados representem efetivamente a população em questão.
Coletar os dados. Devemos ser extremamente cautelosos, para minimizar os erros que podem resultar de uma coleta tendenciosa de dados.
Analisar os dados e tirar conclusões. Identificar também possíveis fontes de erros.
Os estudos que requerem métodos estatísticos decorrem tipicamente de duas fontes comuns: estudos observacionais e experimentais.
Estudo observacional – verificamos e medimos características específicas, mas não tentamos manipular ou modificar os elementos a serem estudados. Ex: plebiscito sobre porte de arma de fogo.
Estudo experimental – aplicamos determinado tratamento e passamos então a observar seus efeitos sobre os elementos as serem pesquisados. Ex: tratamento médico a um determinado grupo de pacientes a fim de determinar sua eficiência na cura
Ao se estudar as características de uma população, o ideal seria investigar todos os elementos dessa população. Porém, na grande maioria dos casos, é inviável estudar a população em virtude de distâncias, custo, tempo, logística, entre outros motivos. A alternativa praticada nestes casos é o trabalho com uma amostra confiável.
Geralmente é representada por N. Corresponde ao conjunto de todos os elementos relativos a um determinado fenômeno que possuem pelo menos uma característica em comum, a população é o conjunto Universo.
Em outras palavras, é o conjunto de todos os indivíduos ou objetos que fazem ou que podem fazer parte de um estudo ou pesquisa.
Geralmente é representada por n. É um subconjunto da população. A amostra deve ser selecionada seguindo certas regras e deve ser representativa, de modo que ela represente todas as características da população como se fosse uma fotografia desta.
Em outras palavras, são os elementos da população estatística que serão analisados, entrevistados ou pesquisados.
Na maioria das vezes, a população Estatística não coincide com a população Geográfica. Por exemplo: se quisermos realizar uma pesquisa para saber a intenção de voto para presidente da república, a nossa população estatística corresponde a todos os brasileiros? A resposta é NÃO! A população Estatística corresponde a todos os brasileiros que são eleitores. Ou seja, pessoas com menos de 16 anos, por exemplo, não fazem parte da população Estatística (embora pertençam à população Geográfica).
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
É qualquer informação retirada de uma população ou amostra, podendo ser através de Censo ou Amostragem.
Recenseamento (Censo): é a contagem oficial e periódica dos indivíduos de um País, ou parte de um País. Ele abrange, no entanto, um leque mais vasto de situações. Assim, pode-se definir recenseamento do seguinte modo:
“estudo científico de um universo de pessoas, instituições ou objetos físicos com o propósito de adquirir conhecimentos, observando todos os seus elementos, e fazer juízos quantitativos acerca de características importantes desse universo”.
Amostragem: é o processo que procura extrair da população elementos que através de cálculos probabilísticos ou não, consigam prover dados inferências da população-alvo. Este processo deve seguir um método criterioso e adequado.
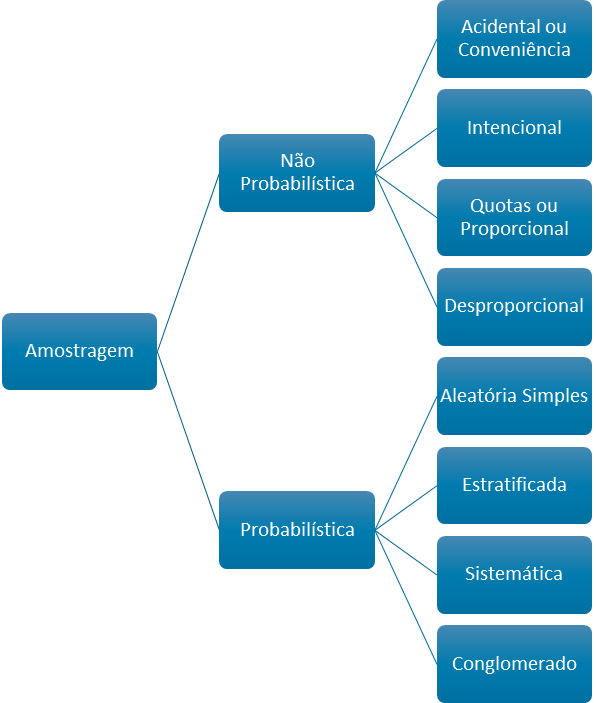
Os principais tipos de amostragem estão representados no diagrama a seguir:
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
A escolha de um método não probabilístico, via de regra, sempre encontrará desvantagem frente ao método probabilístico. No entanto, em alguns casos, se faz necessário a opção por este método. Fonseca (1996), alerta que não há formas de se generalizar os resultados obtidos na amostra para o todo da população quando se opta por este método de amostragem. Isto porque os elementos da amostra não têm a mesma probabilidade de serem escolhidos e, por isso, não é possível fazer inferências sobre a população. Alguns modelos de amostragem não probabilística são:
Indicada para estudos exploratórios. Frequentemente utilizados em supermercados para testar produtos ou em pesquisas de opinião geralmente realizada em locais onde há um grande fluxo de pessoas.
Neste tipo de amostragem, geralmente o entrevistador aborda indivíduos que passem próximo a ele, de forma casual, ou ainda, totalmente acidental.
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
O entrevistador dirige-se a um grupo em específico para saber sua opinião. Por exemplo, quando, de um estudo sobre automóveis, o pesquisador procura apenas oficinas.
Podemos pensar, ainda, que a amostragem intencional é um tipo de acidental utilizando uma espécie de “filtro”. Se a pesquisa consiste em saber, por exemplo, sobre o design de armações de óculos de grau, é natural que o entrevistador procure abordar apenas pessoas que passem próximo a ele e que estejam usando óculos.
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
Na realidade, trata-se de uma variação da amostragem intencional. Necessita-se ter um prévio conhecimento da população e sua proporcionalidade. Por exemplo, deseja-se entrevistar apenas indivíduos da classe A, que representa 12% da população. Esta será a quota para o trabalho.
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
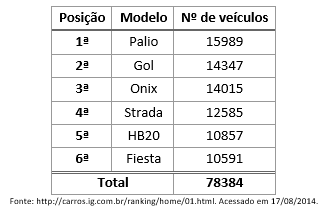
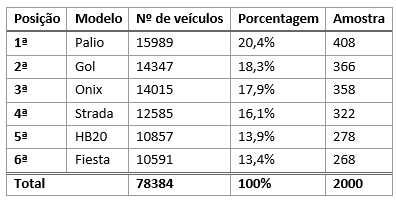
A amostragem proporcional buscará entrevistar pessoas de forma acidental ou intencional e que façam parte do grupo (categoria) específico. Por exemplo, se estamos realizando uma pesquisa sobre o grau de satisfação de proprietários de veículos, devemos, inicialmente, determinar a quantidade de participação na população de cada um dos carros analisados. No mês de julho de 2014, os 6 veículos mais vendidos no Brasil foram:
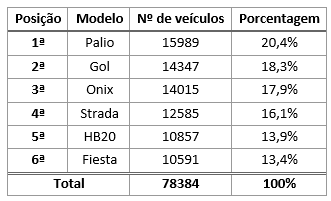
Dessa forma, baseado no total da tabela, podemos calcular as porcentagens de proprietários de cada um dos veículos na população:
Vamos admitir que faremos uma pesquisa de amostra igual a 2000 indivíduos. Qual será a quantidade de pessoas proprietárias de cada um dos modelos listados que devemos entrevistar de maneira intencional? Basta calcularmos as quantidades correspondentes a cada um dos modelos baseado na porcentagem populacional:
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
IMPORTANTE: uma outra questão se refere o fato de os cálculos e arredondamentos feitos possam gerar um valor diferente do total para a amostra. Neste caso, será preciso fazer uma alteração "manual" em um dos valores calculados. Normalmente, o mais adequado é que se altere o maior valor de todos. No vídeo, a seguir, há uma explicação para tal lógica.
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
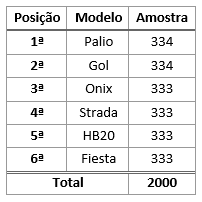
Muito utilizada quando a escolha da amostra for desproporcional à população. De modo geral, este método de amostragem só deve ser realizado quando não se conhece o tamanho real da população correspondente a cada categoria analisada. Por exemplo, considere a tabela anterior a respeito dos 6 veículos mais vendidos no Brasil no mês de julho de 2014. Caso não tivéssemos acesso às porcentagens populacionais, poderíamos realizar uma pesquisa com 2000 pessoas da seguinte maneira:
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
Para que se possam realizar inferências sobre a população, é necessário que se trabalhe com amostragem probabilística. É o método que garante segurança quando se investiga alguma hipótese. Normalmente os indivíduos investigados possuem a mesma probabilidade de ser selecionado na amostra. São tipos de amostragem probabilística:
É o mais utilizado processo de amostragem. Prático e eficaz confere precisão ao processo de amostragem. Normalmente utiliza-se uma tabela de números aleatórios e nomeiam-se os indivíduos, sorteando-se um por um até completar a amostra calculada.
Queremos escolher 10 alunos de 90 alunos de uma sala. Escrevemos números de 1 a 90 em um papel e sorteamos 10 números. Seria o mesmo princípio do “bingo”: sortear 10 número a partir de um globo com bolinhas numeradas de 1 a 90.
Uma maneira de substituir os papéis é utilizar uma tabela de números aleatórios, que podem ser encontradas em livros de Estatística. Porém, esse método já está ultrapassado, visto que temos acesso a softwares (inclusive para smartphones) que fazem sorteios aleatórios. Ou, ainda, funções específicas (como a ALEATÓRIOENTRE presente no Microsoft Excel).
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
Uma maneira de substituir os papéis é utilizar uma tabela de números aleatórios, que podem ser encontradas em livros de Estatística. Porém, esse método já está ultrapassado, visto que temos acesso a softwares (inclusive para smartphones) que fazem sorteios aleatórios. Ou, ainda, funções específicas (como a ALEATÓRIOENTRE presente no Microsoft Excel).
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
Em um grande número de exemplos, o pesquisador depara-se com a população ordenada. Uma palavra chave de fácil memorização é “fichário”: quando temos nossa população cadastrada em fichas numeradas ou, ainda, banco de dados que produzem números sequenciais para cada novo cadastro efetuado.
No caso de uma linha de produção, podemos, a cada dez itens produzidos, retirar um para pertencer a uma amostra de produção diária. Neste caso estaríamos fixando o valor da amostra em 10% da população (amostragem probabilística aleatória simples)
Quando se trabalha com sorteio de quadras de casas, por exemplo, há uma regra crescente para os números das casas. Em casos como este, divide-se a população pela amostra e obtém-se um coeficiente (y). A primeira casa será a de número um x escolhido aleatoriamente, a segunda será a de número x + y; a terceira será a de número x + 2y, a quarta será x + 3y e assim sucessivamente (amostragem probabilística aleatória sistemática).
Observe, se a rua contém 900 casas e desejamos obter uma amostra de 50 casas:
o segundo número será x + 18; o terceiro será x + 2.18; o quarto será x + 3.18, e assim sucessivamente. Se o número sorteado (x) for o número 4 (par), tomaríamos, pelo lado direito da rua o 4º prédio, o 22º, o 40º etc., até voltarmos ao início da rua, pelo lado esquerdo.
Uma clínica possui 200 pacientes (cada um cadastrado com valores de 1 a 200). Deseja-se sortear uma amostra de tamanho 10.
Inicialmente, calculamos o tamanho do “passo” a ser dado na hora de coletar a amostra:
200 : 10 = 20 (é o nosso “passo”)
Agora, sorteamos um número entre 1 e o nosso “passo”, no caso, 20. Suponhamos ter sorteado o número 5. A partir desse valor, somamos o “passo” obtendo os números dos elementos de nossa amostra:
5, 25, 45, 65, 85, 105, 125, 145, 165, 185.
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
Quando se deseja guardar uma proporcionalidade na população heterogênea, estratifica-se cada subpopulação por intermédio de critérios como classe social, renda, idade, sexo, entre outros.
Esse tipo de amostragem é útil quando se pode construir um sistema de referências, mas sabe-se de antemão que existe uma grande variabilidade entre os grupos e uma pequena variabilidade dentro de cada grupo. Com o objetivo de eliminar a variabilidade entre os grupos, convém utilizar este sistema de amostragem. A cada grupo damos o nome de estrato. Depois, retiramos de cada estrato uma amostra casual simples.
Nota: não confunda a palavra estrato com extrato. Do dicionário Michaelis:
Extrato: Produto da extração. Substância extraída de outra. Resumo de um escrito. Cópia resumida; excerto, fragmento, trecho.
Suponha que dos 90 alunos de uma sala, 54 são homens e 36 sejam mulheres. Vamos obter 10% da população para a amostra proporcional estratificada. Então vamos dividir nossa população em dois estratos: homens e mulheres. Destes dois estratos vamos obter 10% de cada um. Assim temos:
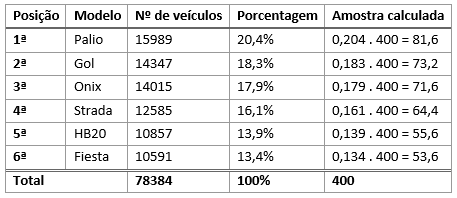
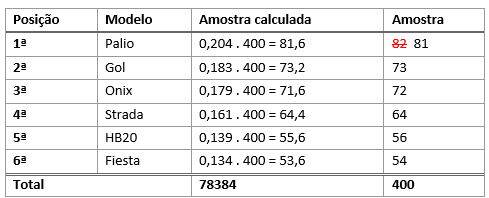
Suponhamos o mesmo caso dos veículos analisado anteriormente. Vamos admitir, agora, que desejamos realizar uma amostra de tamanho 400. Vamos calcular o tamanho da amostra baseado na porcentagem populacional:
Perceba que os valores obtidos para as amostras de cada estrato são valores decimais. Em um processo de amostragem, é impossível entrevistarmos 81,6 pessoas.
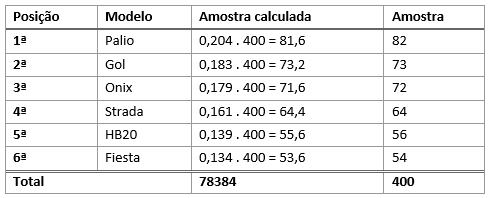
Por isso, devemos arredondar os valores calculados, utilizando as regras de arredondamento convencionais:
Porém, veja que o tamanho da amostra havia sido definido, desde o começo, como sendo igual a 400 e, após os cálculos e arredondamentos, chegamos a uma soma de 401 elementos (82+73+72+64+56+54 = 401). Como nossa amostra deve ser, obrigatoriamente, igual a 400, devemos ajustar os valores manualmente. Esse ajuste consiste e aumentar ou diminuir geralmente 1 ou 2 unidades, preferencialmente no maior valor obtido, que, no caso do exemplo, é igual a 82. Assim, nossa amostra final será:
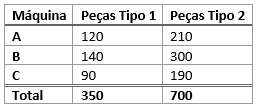
Suponhamos que em uma indústria há 3 máquinas que fabricam dois tipos de peças cada uma. Em um certo dia de produção, as quantidades produzidas pelas máquinas A, B e C das peças Tipo 1 e Tipo 2 foram:
Deseja-se analisar 8% de todas as peças obtidas a fim de controle de qualidade. Realizar uma amostragem estratificada.
Inicialmente, calculamos o tamanho total da amostra de cada um dos tipos de peças:
- 8% de 350 = 0,08 . 350 = 28 peças;
- 8% de 700 = 0,08 . 700 = 56 peças.
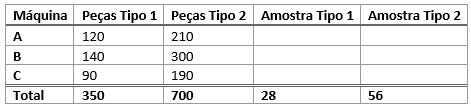
Colocamos os valores obtidos na tabela:
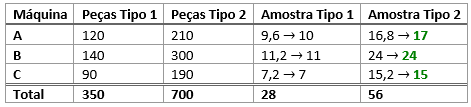
Em seguida, calculamos 8% de cada um dos valores da tabela. A primeira linha da tabela é obtida fazendo:
- 8% de 120 = 0,08 . 120 = 9,6
- 8% de 210 = 0,08 . 210 = 16,8.
Realizando todos os cálculos, obteremos os valores apresentados em vermelho. Os valores em vermelho são, em sua maioria, decimais. Fazemos, assim, o arredondamento de tais valores, obtendo os valores em verde.
Para checar, somamos os valores em verde de cada coluna e conferimos se é igual ao total:
- Amostra Tipo 1: 10 + 11 + 7 = 28
- Amostra Tipo 2: 17 + 24 + 15 = 56
Caso uma dessas somas não fosse igual ao total (28 e 56), deveríamos realizar um ajuste nos maiores valores de cada coluna, conforme já explicado anteriormente.
A resposta para o nosso exemplo serão os valores marcado em verde na tabela. Em seguida, devemos sortear as quantidades indicadas de cada tipo de peça para cada uma das três máquinas de maneira aleatória.
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
Muitas vezes a construção do sistema de referência é impossível. Nesta modalidade de amostragem, divide-se a área da população em seções (ou conglomerados): em seguida sorteia-se algumas dessas seções e, finalmente são estudados todos os elementos das seções escolhidas.
Queremos estudar a população que habita uma favela, mas não temos meios de conseguir uma relação completa dos habitantes. Porém, temos a relação completa dos barracos que compõem a favela. Barraco é uma unidade de amostragem maior, que engloba um certo número de indivíduos. Logo, podemos escolher uma amostra casual simples de barracos e estudarmos todos os indivíduos que moram nos barracos sorteados. Ao conjunto de indivíduos que moram em um barraco damos o nome de conglomerado.
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
Dados estatísticos: é qualquer característica que possa ser observada ou medida de alguma maneira. As matérias-primas da estatística são os dados observáveis.
Variável: é o que se deseja observar para se tirar algum tipo de conclusão. Geralmente as variáveis para estudo são selecionadas por processos de amostragem. Os símbolos utilizados para representá-las são letras maiúsculas do alfabeto, tais como X, Y, Z,... que podem assumir qualquer valor de um conjunto de dados.
Para podermos decidir como organizar os dados é preciso saber com que tipo de variáveis estamos trabalhando.
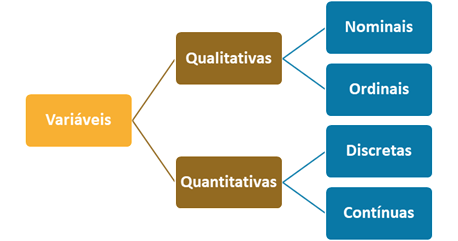
Os tipos de variáveis são:
- quantitativas que podem ser discretas ou contínuas;
- qualitativas que podem ser ordinais ou nominais.
Veja o diagrama:
As variáveis quantitativas discretas assumem valores pontuais. Por exemplo, a idade das pessoas em anos. Neste caso, a idade representa valores bem definidos como 20, 21, 22, 23 anos.
As variáreis quantitativas contínuas assumem valores dentro de um intervalo. Por exemplo, podemos considerar a massa das pessoas em gramas. É claro que uma pessoa pode ter 60 235 gramas ou 60 236 gramas. Caberia a pergunta: não seria uma variável discreta? Neste caso, temos um conjunto muito grande de valores que essa variável pode assumir tornando-a contínua.
As variáveis qualitativas ordinais são aquelas que atribuem qualidades de modo que possam ser ordenadas de maneira hierárquica. Por exemplo, o grau de escolaridade: analfabeto, 1° grau incompleto, 1° grau completo, 2° grau incompleto e assim por diante.
Por fim, as variáveis qualitativas nominais são aquelas que atribuem qualidade mas que não é possível fazer uma ordenação. Por exemplo, matéria do colégio que mais gostava: Matemática, Física, Biologia, História...
É importante ressaltar que não existem regras fixas para se dizer que uma variável é discreta ou contínua. Muitas vezes, podemos dar tanto um tratamento contínuo à variável idade quanto um tratamento discreto. Tal decisão depende do que se quer analisar e da quantidade de dados envolvida. Por exemplo: se estivermos fazendo uma pesquisa numa festa e encontramos jovens de 18 a 25 anos, podemos considerar a variável idade como discreta, ou seja, podemos contar exatamente quantas pessoas há com 18, 19, 20, 21, 22, 23, 24 e 25 anos. Porém, imaginemos que numa outra festa, com 1000 convidados, encontrássemos pessoas de 3 à 80 anos. É claro que poderíamos contar o número de indivíduos com 3,4,5,6,..., 79 e 80 anos. Porém, muitas vezes, nosso interesse está em analisar algumas faixas etárias. Por exemplo:
Nesse caso, a variável idade passa a receber um tratamento contínuo. Assim, é preciso tomarmos muito cuidado com o fato de que algumas pessoas defendem que a variável IDADE é discreta. Dependendo do tratamento dado a ela, podemos transformá-la de discreta para contínua.
Vejamos um outro caso: suponhamos um fabricante de tintas, que produz tintas coloridas fazendo o uso da tinta branca+pigmentos. Suponhamos, ainda, que ele trabalhe com as seguintes cores: branco, amarelo, vermelho, azul e preto. Aparentemente, a variável COR é qualitativa nominal. Porém, esse fabricante afirma que o pigmento amarelo é mais barato que o vermelho e que para se produzir tinta azul se usa muito corante (e mais corante ainda para tinta preta). Isso faz com que os custos sejam elevados para a tinta preta e reduzidos para a branca. Neste caso, podemos estabelecer uma ordem crescente para os custos:
1°) branco
2°) amarelo
3°) vermelho
4°) azul
5°) preto
Percebemos que foi estabelecida uma ordem. Assim, a variável COR é, agora, qualitativa ordinal.
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
Para efeitos de análise, foi passado um questionário para uma amostra de 30 ouvintes de uma determinada palestra. Pediu-se para que respondessem com a maior exatidão possível. Um modelo do questionário é mostrado a seguir.
Questionário
Procure responder às questões com a maior exatidão possível.
Não deixe questões em
branco!
1) Sexo: ( ) masculino ( )
feminino
2) Idade (em anos): _____
3) Altura (em metros):
________ m
4) Peso (em quilos): ______
kg
5) Número de irmãos
(vivos): _____
6) Fuma atualmente? ( )
SIM ( ) NÃO
7) Qual a sua tolerância
quanto à fumaça do cigarro?
( ) Muito tolerante (
) Pouco tolerante ( ) Indiferente
8) Número de horas médias
por semana que pratica exercícios e atividades físicas (academia, andar,
correr, alongamento, esportes, etc): ______ horas
9) Qualidade da programação
atual da Rede Globo:
( ) Boa
( ) Regular ( )
Péssima ( ) Não sabe
É importante destacar alguns pontos importantes a respeito do questionário:
Deve-se ter muito cuidado na elaboração das questões para que não gerem ambiguidades quanto à interpretação nem problemas de respostas diferentes que não possibilitem uma análise posterior.
O resultado de um questionário nem sempre corresponde à realidade, visto que a pessoa pode não saber ao certo sua altura ou fazer muito tempo que não se pesa.
Alguns cuidados especiais devem ser tomados na elaboração de questões “abertas”, ou seja, que não são do tipo teste, para que as respostas sejam padronizadas. Por exemplo, se não for especificado, uma pessoa pode responder que a sua altura é de 172 cm e outra de 1,72 m. Ou ainda, o que seria muito pior pois alteraria o resultado da pesquisa, é no caso de perguntar o número de irmãos: uma pessoa pode ter 4 irmãos vivos e 1 que faleceu. Qual valor ela deveria colocar no questionário: 4 ou 5? Daí a necessidade da especificação.
Vale a pena, também, ficar atento a perguntas do tipo: “você gosta de carros brancos? ( ) sim ( ) não”. Aparentemente não há nenhum problema nessa pergunta, porém, uma análise mais cuidadosa faria perceber que o entrevistado poderia responder “não, não gosto de carros brancos, prefiro os vermelhos” como poderia responder “não, não gosto de carros, prefiro motos”. Porém, essa diferença de respostas não seria detectada com a pergunta (ambígua) acima. Neste caso, devemos reformular tal pergunta ou fazer outras confirmatórias. Embora isso não seja tratado neste texto, alertamos quanto ao fato na hora de elaborar e responder um questionário.
O resultado de tal questionário em uma amostra de tamanho 30 é mostrado na tabela a seguir. As variáveis em questão são:
Sexo – masculino (M) ou feminino (F)
Idade – em anos
Altura – em metros
Peso – em quilos
Irmãos – número de irmãos vivos
Fuma – é fumante (SIM) ou não é fumante (NÃO)
Tolerância – nível de tolerância à fumaça do cigarro: muito tolerante (M), pouco tolerante (P) ou indiferente (I)
Exercícios – número médio de horas que pratica atividades físicas por semana
Qualidade – qualidade da programação atual da Rede Globo: boa (B), regular (R), péssima (P) ou não sabe (N)
A partir da tabela a seguir, onde estão representados os dados brutos (ou seja, aqueles obtidos a partir do questionário), percebemos que há uma certa dificuldade de, por exemplo, dizer se a maioria das pessoas é muito ou pouco tolerante ao fumo, ou quanto ao número médio de horas que as pessoas praticam atividades físicas. Tal dificuldade já se apresenta com um pequeno conjunto de dados (apenas 30 entrevistados). Para conjuntos maiores, diria que é praticamente impossível tirar alguma conclusão apenas observando os dados brutos.
Daí a necessidade de reorganizarmos os dados em tabelas e gráficos. A organização em tabelas deve ser a mais simples possível, evitando-se utilizar tabelas muito incrementadas ou coloridas. A forma como esses dados serão organizados também pode variar, de acordo com os interesses e do que se quer analisar. Assim, daremos aqui, alguns exemplos de organização e tipos de gráficos.
Aliás, quanto aos gráficos, nem sempre há um gráfico correto e outro errado. Para representar um conjunto de dados, muitas vezes é possível usar mais de um tipo de gráfico. O melhor é aquele que mais enfatiza o resultado que você deseja apresentar, ou seja, que dá maior destaque às informações que você julga importantes.
Baseado na classificação de variáveis que apresentamos, podemos dizer que são:
SEXO – nominal
IDADE – discreta
ALTURA – contínua (pois assume uma grande variedade de valores, embora possamos considerá-la discreta)
PESO – discreta
IRMÃOS – discreta
FUMA – nominal
TOLERÂNCIA – nominal
EXERCÍCIOS – discreta
QUALIDADE – ordinal
As variáveis podem ser classificadas dos seguintes modos:
1) Qualitativas (ou atributos): são características de uma população que não podem ser medidas, sendo classificadas em nominais ou ordinais.
- Nominal: são utilizados símbolos, ou números, para representar determinado tipo de dados, mostrando, assim, a qual grupo ou categoria eles pertencem, como sexo, nacionalidade, etc.
- Ordinal: quando uma classificação for dividida em categorias ordenadas em graus convencionados, havendo uma relação entre as categorias do tipo “maior do que”, “menor do que”, “igual a”, primeiro, segundo, terceiro e assim sucessivamente.
2) Quantitativas: são características populacionais que podem ser quantificadas, sendo classificadas em discretas e contínuas.
- Discretas: são aquelas variáveis que podem assumir somente valores inteiros num conjunto de valores. É gerada pelo processo de contagem, como o número de veículos que passa em um posto de gasolina, o número de estudantes nesta sala de aula.
- Contínuas: são aquelas variáveis que podem assumir um valor dentro de um intervalo de valores. É gerada pelo processo de medição. Neste caso serve como exemplo o volume de água em um reservatório ou o peso de um pacote de cereal.
Uma questão importante a ser compreendida por todos os estudantes de Estatística é quanto ao arredondamento. Raramente um cálculo realizado será exato. O mais comum é que os resultados obtidos tenham várias casas decimais.
O primeiro ponto a ser discutido é: “quantas casas decimais eu devo utilizar?” Não há uma regra definida para isto. O que vale, aqui, é utilizar a coerência e o bom senso. Por exemplo, suponhamos que estamos trabalhando o cálculo de valores monetários, em reais. O que faz mais sentido neste caso é trabalharmos com 2 casas após a vírgula, visto que a terceira casa após a vírgula não faz sentido, ou seja, R$ 3,451 impossibilita, na prática, o pagamento de R$ 0,001. Neste caso, o melhor é utilizarmos R$ 3,45. Um outro exemplo: se estivermos trabalhando com medidas efetuadas com a régua, podemos utilizar até 2 casas após a vírgula, ou seja, faz sentido apresentarmos um resultado do tipo 5,43 cm, visto que estaríamos dizendo que a medida obtida tem 5 centímetros, 4 milímetros e 3 décimos de milímetro (este valor indicaria a incerteza da medida). Porém, não vamos discutir nesta apostila incertezas e erros quando utilizamos instrumentos de precisão.
Um segundo ponto a ser notado é a respeito de qual regra de arredondamento devemos utilizar. Existem várias maneiras de fazermos o arredondamento de um número, porém, vamos utilizar o método tradicional de arredondamento que nos diz: quando a casa decimal seguinte àquela que vamos arredondar for 0, 1, 2, 3 ou 4, esta casa decimal permanece como está. Se a casa decimal seguinte for 5, 6, 7, 8 ou 9, somamos 1 à casa decimal a ser arredondada. Vejamos alguns exemplos.
Arredondar 23,4581 para 3 casas decimais. Note que a quarta casa é 1 (menor que 5) . Logo, a casa a ser arredondada, que é o número 8, permanece igual. Assim, após o arredondamento, temos o número 23,458.
Arredondar 3,276 para duas casas decimais. Verificamos que a terceira casa é 6 (maior ou igual a 5). Logo, devemos somar 1 à segunda casa decimal. Após o arredondamento o número fica 3,28.
Arredondar 12,49999 para 1 casa decimal. Como o número da segunda casa decimal é maior ou igual a 5, adicionamos 1 unidade ao valor a ser arredondado, ou seja, 4+1=5. Logo, o número após o arredondamento fica 12,5.
Arredondar para 2 casas decimais o número 35,89076. Como na terceira casa temos o zero, mantemos o valor da segunda casa, ou seja, o número após arredondamento fica 35,89.
Arredondar para 2 casas decimais o número 0,39601. Como na terceira casa decimal temos um valor superior a 5, devemos somar 1 unidade ao valor da segunda casa. Note, porém, que na segunda casa decimal temos o número 9. Pensemos, então, no número 39 (1ª + 2ª decimais). Somando 1 a esse número, teremos 40. Logo, o número arredondado fica 0,40.
Muito cuidado! Não existem arredondamentos sucessivos em um mesmo número. É considerado ERRADO executar tal prática.
Por exemplo: suponhamos o número 6,847e queremos arredondá-lo para 1 casa decimal. Inicialmente, arredondamos para duas casas obtendo o número 6,85. Agora, arredondamos para 1 casa obtendo 6,9. Esse arredondamento está errado, pois foram executados dois arredondamentos sucessivos no mesmo número. O correto é: o valor da segunda casa decimal é 4, logo o número arredondado corretamente deve ser 6,8.
AO FINAL DA PÁGINA VOCÊ ENCONTRARÁ AS RESPOSTAS DOS EXERCÍCIOS
1) Classifique em verdadeiro ou falso as seguintes informações:
a) Estatística é um conjunto de técnicas destinadas a organizar um conjunto de dados.
b) Sempre que estivermos trabalhando com números, deveremos utilizar a Inferência Estatística.
c) A Estatística Descritiva fornece uma maneira adequada de tratar um conjunto de valores, numéricos ou não, com a finalidade de conhecermos o fenômeno de interesse.
d) Qualquer amostra representa, de forma adequada, uma população.
e) As técnicas estatísticas não são adequadas para casos que envolvem experimentos destrutivos como, por exemplo, queima de equipamentos, destruição de corpos de provas, etc.
2) Um pesquisador está interessado em fazer um levantamento sobre alguns aspectos socioeconômicos dos empregados da Companhia MK. Escolha 4 variáveis a serem pesquisadas identificando se são qualitativas ou quantitativas.
3) Classifique as variáveis em qualitativas (nominais/ordinais) ou quantitativas (discretas/ contínuas):
a) cor dos cabelos dos alunos de uma escola.
b) número de filhos de casais residentes em uma determinada rua.
c) o ponto obtido em cada jogada de um dado.
d) naturalidade das pessoas que vivem na cidade de São Paulo.
e) escolaridade dos funcionários de uma empresa.
f) classe social.
g) patentes do exército.
h) cargo na empresa.
i) número de quilômetros percorridos entre a sua casa e o trabalho.
j) tempo, em segundos, que cada trabalhador de uma indústria leva para montar determinado equipamento.
4) Diga se variáveis são discretas, contínuas, ordinais ou nominais: salários, sexo dos filhos, número de peças defeituosas produzidas por uma máquina, altura de pessoas, grau de instrução, número de filhos, peso.
5) Uma marca de vinho branco importada é vendida na maior parte dos supermercados do país. Desejando saber o preço médio de venda, o distribuidor deseja usar uma amostragem aleatória com 45 pontos de venda. Especifique um plano de amostragem que pode ser utilizado.
6) Suponha que se tenha uma tabela com a relação das 400 maiores empresas do país, no ano de 2005, por volume de vendas, listadas em ordem alfabética. Desejando uma amostra aleatória de 40 elementos. Qual o tipo de amostragem que se pode utilizar?
7) Classifique o tipo de amostragem utilizada em cada caso:
a) Em uma sala de aula composta por 60 alunos arrumados em 6 fileiras de 10 alunos cada, toma-se uma amostra de 10 alunos jogando-se um dado e escolhendo os alunos da fileira correspondente ao resultado da jogada.
b) Em uma sala de aula composta por 60 alunos, toma-se uma amostra de 10 alunos escolhendo-se um valor qualquer na lista de chamada e selecionando os 10 alunos a partir daquele número. Se chegar ao fim da lista antes de completar 10 alunos, volta-se ao início da lista, até completar 10 alunos.
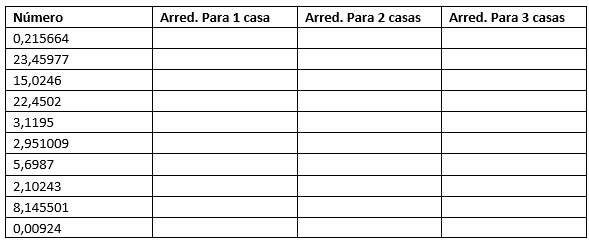
8) Complete a tabela a seguir arredondando os números dados para a quantidade de casas decimais indicadas:
9) O diretor de uma escola, na qual estão matriculados 280 meninos e 320 meninas, desejoso de conhecer as condições de vida extraescolar de seus alunos e não dispondo de tempo para entrevistar todas as famílias, resolve fazer um levantamento por amostragem, em 10% dessa clientela. Obtenha, para esse diretor, os elementos componentes da amostra.
10) Em uma escola existem 250 alunos, distribuídos conforme quadro. Obtenha uma amostra proporcional estratificada de 40 alunos.
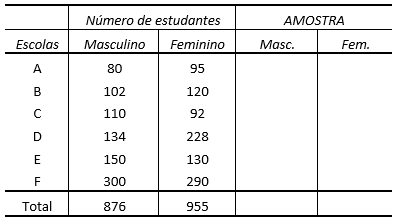
11) Uma cidade X apresenta o seguinte quadro relativo às suas escolas de Ensino Fundamental. Obtenha uma amostra proporcional estratificada de 120 estudantes.
12) Classifique as variáveis em qualitativas (nominal ou ordinal) ou quantitativas (discreta ou contínua):
a) número de ações negociadas por dia na bolsa de valores ao longo de 1 ano;
b) número de filhos de um certo casal;
c) comprimento dos pregos produzidos por uma máquina;
d) número de volumes na biblioteca da faculdade;
e) salário dos funcionários de uma empresa;
f) cor predominante da parede externa de sua casa;
g) grau de escolaridade;
h) número de horas dormidas na última noite;
i) tipo de comida preferida;
j) cargo dos funcionários de uma empresa.
13) Em um local de exame da FUVEST existem 150 funcionários, distribuídos segundo seus cargos conforme tabela. Obtenha uma amostra proporcional estratificada de 30 funcionários.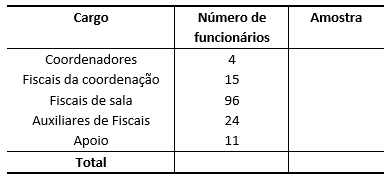
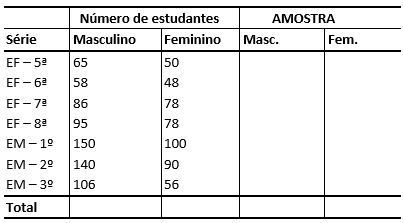
14) Uma escola apresenta a seguinte distribuição de alunos para o ensino fundamental (EF) e ensino médio (EM). Obtenha uma amostra proporcional estratificada de 130 estudantes.
15) Uma população encontra-se em três estratos, com tamanhos, respectivamente, n1 = 40, n2 = 100 e n3 = 60. Sabendo que, ao ser realizada uma amostragem estratificada proporcional, nove elementos da amostra foram retirados do 3o estrato, determine o número total de elementos da amostra.
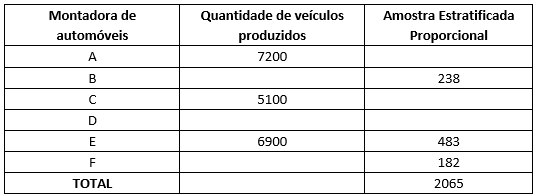
16) A tabela abaixo mostra a performance de 6 montadoras de automóveis em um determinado mês do ano de 2005. Sabendo-se que foram retiradas amostras estratificadas proporcionais, complete a tabela:
17) Um fabricante de computadores produz 8700 máquinas por mês. O departamento de qualidade necessita de uma amostra sistemática de 30 peças para teste. Sabendo que a 1ª máquina selecionada foi a nº 12, então as próximas 4 máquinas foram respectivamente: (considere que todas as máquinas estão numeradas de 0001 a 8700) (Justifique a resposta).
a) 24, 36, 48, 60
b) 42, 72, 102, 132
c) 302, 592, 882, 1172
d) 290, 580, 870, 1160
18) A produção diária de uma indústria é de 450 peças. Uma amostra sistemática de tamanho 30 será extraída de uma produção, começando pela peça de número 10. Assinale a alternativa correspondente aos números das cinco primeiros peças: (justifique a resposta)
a) 10 – 25 – 40 – 55 – 70
b) 10 – 15 – 20 – 25 – 30
c) 10 – 12 – 14 – 16 – 18
d) 10 – 20 – 30 – 40 – 50
19) Em uma empresa existem 808 funcionários, distribuídos segundo seus cargos conforme tabela. Obtenha uma amostra proporcional estratificada de 20% dos funcionários para a realização de uma pesquisa. Justifique os cálculos.
1) a) V b) F c) V d) F e) F
2) resposta pessoal
3) a) nominal
b) discreta
c) discreta
d) nominal
e) ordinal
f) ordinal
g) ordinal
h) ordinal
i) discreta (pode ser contínua dependendo da interpretação)
j) contínua
4) continua, nominal, discreta, contínua, ordinal, discreta, contínua.
5) Proporcional ou estratificada
6) Sistemática
7) a) conglomerado
b) sistemática
8)
|
Número |
Arred. Para 1 casa |
Arred. Para 2 casas |
Arred. Para 3 casas |
|
0,215664 |
0,2 |
0,22 |
0,216 |
|
23,45977 |
23,5 |
23,46 |
23,460 |
|
15,0246 |
15,0 |
15,02 |
15,025 |
|
22,4502 |
22,5 |
22,45 |
22,450 |
|
3,1195 |
3,1 |
3,12 |
3,120 |
|
2,951009 |
3,0 |
2,95 |
2,951 |
|
5,6987 |
5,7 |
5,70 |
5,699 |
|
2,10243 |
2,1 |
2,10 |
2,102 |
|
8,145501 |
8,1 |
8,15 |
8,146 |
|
0,00924 |
0,0 |
0,01 |
0,009 |
9) 28 homens e 32 mulheres
10)
|
Séries |
Número de alunos |
AMOSTRA |
|
1a |
35 |
6 |
|
2a |
32 |
5 |
|
3a |
30 |
5 |
|
4a |
28 |
4 |
|
5a |
35 |
6 |
|
6a |
32 |
5 |
|
7a |
31 |
5 |
|
8a |
27 |
4 |
|
Total |
250 |
40 |
11)
|
|
Número de estudantes |
AMOSTRA |
||
|
Escolas |
Masculino |
Feminino |
Masc. |
Fem. |
|
A |
80 |
95 |
5 |
6 |
|
B |
102 |
120 |
7 |
8 |
|
C |
110 |
92 |
7 |
6 |
|
D |
134 |
228 |
9 |
15 |
|
E |
150 |
130 |
10 |
9 |
|
F |
300 |
290 |
19 |
19 |
|
Total |
876 |
955 |
57 |
63 |
12) a) contínua b) discreta c) contínua d) discreta e) contínua f) nominal g) ordinal h) discreta i) nominal j) ordinal
13)
|
Cargo |
Número de funcionários |
Amostra |
|
Coordenadores |
4 |
1 |
|
Fiscais da coordenação |
15 |
3 |
|
Fiscais de sala |
96 |
19 |
|
Auxiliares de Fiscais |
24 |
5 |
|
Apoio |
11 |
2 |
|
Total |
150 |
30 |
14)
|
|
Número de estudantes |
AMOSTRA |
||
|
Série |
Masculino |
Feminino |
Masc. |
Fem. |
|
EF – 5ª |
65 |
50 |
7 |
5 |
|
EF – 6ª |
58 |
48 |
6 |
5 |
|
EF – 7ª |
86 |
78 |
9 |
8 |
|
EF – 8ª |
95 |
78 |
10 |
8 |
|
EM – 1º |
150 |
100 |
17* |
12* |
|
EM – 2º |
140 |
90 |
15* |
10 |
|
EM – 3º |
106 |
56 |
12 |
6 |
|
Total |
700 |
500 |
76 |
54 |
15) 6+15+9 = 30
16)
|
Montadora de automóveis |
Quantidade de veículos produzidos |
Amostra Estratificada Proporcional |
|
A |
7200 |
504 |
|
B |
3400 |
238 |
|
C |
5100 |
357 |
|
D |
4300 |
301 |
|
E |
6900 |
483 |
|
F |
2600 |
182 |
|
TOTAL |
29500 |
2065 |
17) C
18) A
19) Tamanho da amostra = 162 sendo: Gerentes = 2; Coordenadores = 6; Supervisores = 26; Atendentes = 128
Faça o download gratuito da apostila sobre Introdução à Estatística em formato PDF.
Baixe AgoraVocê também pode se interessar por:
ROL, tabelas de frequências, classes (intervalos), determinação do número de classes em uma tabela, Regra de Sturges e lista de exercícios
Gráficos de linhas, colunas, barras, setores (pizza ou torta), gráfico de dispersão, diagrama ramo-e-folhas, pictograma, histograma, polígono de frequências e lista de exercícios
Fórmulas e cálculos da média, moda e mediana e lista de exercícios