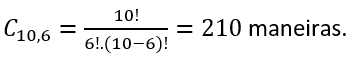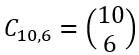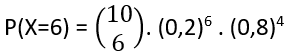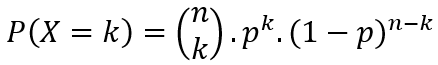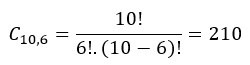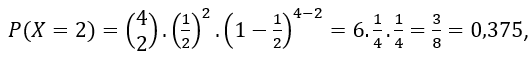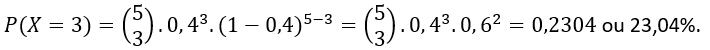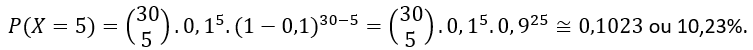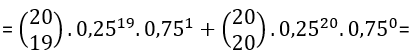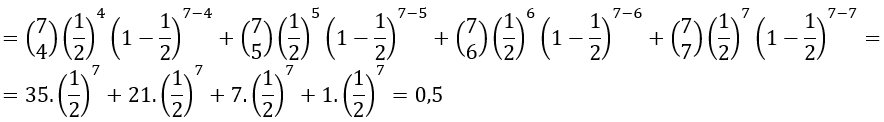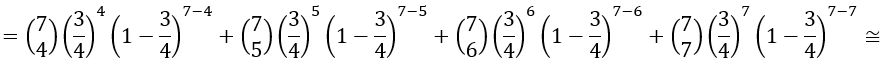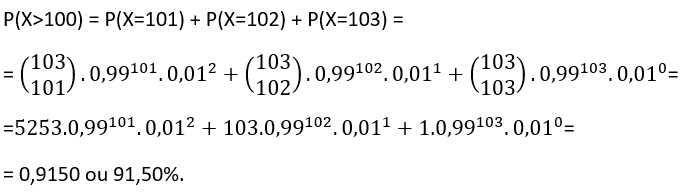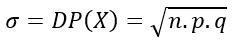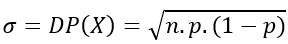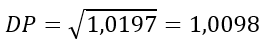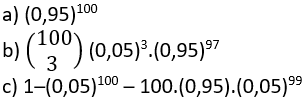Conrad Elber Pinheiro
Professor Guru
Atualizado em 28/07/2023
1. Lei binomial da probabilidade - Ensaios de Bernoulli
Exemplos de ensaio de Bernoulli
2. Distribuição Binomial
Resumo da Distribuição Binomial
2.1. Cálculo do número binomial (combinação de n elementos tomados k a k)
2.2. Cálculo de uma combinação C(n,k) SEM calculadora
2.3. Cálculo de uma combinação C(n,k) USANDO uma calculadora científica
Regras para eventos complementares
3. Valor Esperado ou Esperança da distribuição Binomial
4. Variância e Desvio Padrão de uma distribuição Binomial
5. Lista de Exercícios
Respostas dos Exercícios
Ao final desta página, você pode fazer o download gratuito da apostila sobre Distribuição Binomial em formato PDF.
Clique aqui para assistir a playlist com os conteúdos desta página no YouTube
Consideremos um experimento que consiste em uma sequência de ensaios ou tentativas independentes, isto é, ensaios nos quais a probabilidade de um resultado em cada ensaio não depende dos resultados ocorridos nos ensaios anteriores, nem dos resultados nos ensaios posteriores. Em cada ensaio, podem ocorrer apenas dois resultados, um deles que chamaremos de sucesso (S) e outro que chamaremos de fracasso (F). À probabilidade de ocorrer sucesso em cada ensaio chamaremos de p; a probabilidade de fracasso chamaremos de q, de tal modo que q=1–p. Tal tipo de experimento recebe o nome de ensaio de Bernoulli.
1) Uma moeda é lançada 5 vezes. Cada lançamento é um ensaio, em que dois resultados podem ocorrer: cara ou coroa. Chamemos de sucesso o evento sair uma cara e de fracasso o evento sair uma coroa. Em cada ensaio, p=0,5 e q=0,5.
2) Uma urna contém 4 bolas vermelhas e 6 brancas. Uma bola é extraída, observada sua cor e reposta na urna; este procedimento é repetido 8 vezes. Cada extração é um ensaio, em que dois resultados podem ocorrer: bola vermelha ou bola branca. Chamemos de sucesso o evento sair bola vermelha. Consequentemente, fracasso corresponde ao evento sair bola branca. Neste caso, p = 4/10 e q = 6/10.
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
Antes de apresentarmos a fórmula e suposições da distribuição Binomial de probabilidades, vamos analisar um exemplo e deduzir a fórmula a partir dele.
Uma prova consta de 10 testes com 5 alternativas cada um, sendo apenas uma delas correta. Um aluno que nada sabe a respeito da matéria avaliada, “chuta” uma resposta para cada teste. Qual é a probabilidade de ele acertar exatamente 6 testes?
A probabilidade de acertar um teste aleatoriamente é 1/5 = 0,2. Logo, a de errar esse teste é de 1 - 1/5 = 4/5 = 0,8.
Vamos considerar uma situação bastante específica: o aluno acerta os testes de 1 à 6 e erra os testes de 7 à 10. A probabilidade de isso acontecer é obtida utilizando–se o Princípio Fundamental da Contagem:
0,2 . 0,2 . 0,2 . 0,2 . 0,2 . 0,2 . 0,8 . 0,8 . 0,8 . 0,8 =
= (0,2)⁶ . (0,8)⁴ = 0,000026 ou 0,0026%.
Porém, essa é apenas uma situação de acertos / erros possíveis. O número total de maneiras que esse aluno pode acertar 6 testes de um total de 10 testes é calculada utilizando–se combinação (visto que a ordem dos acertos NÃO importa):
Para cada uma dessas 210 formas, temos uma probabilidade de acerto igual a calculada anteriormente. Logo, a probabilidade de esse aluno acertar 6 testes qualquer é:
210 . (0,2)⁶ . (0,8)⁴ = 0,0055 ou 0,55%.
Vamos definir a variável aleatória X que representa sucesso como sendo:
X: número de testes que o aluno acerta (sucesso).
Associada a X, temos a probabilidade de sucesso p=0,2 e, consequentemente, a probabilidade de fracasso q=1–0,2=0,8 (probabilidade de errar o teste).
Lembrando que
podemos escrever que a probabilidade do aluno acertar 6 testes é:
Generalizando podemos deduzir a fórmula da distribuição Binomial: se em cada uma das n repetições de Ensaios de Bernoulli a probabilidade de ocorrer um evento definido como sucesso é sempre p, a probabilidade de que esse evento ocorra em apenas k das n repetições é dada por:
Um experimento binomial deve satisfazer os seguintes critérios:
1) O experimento é repetido n vezes, onde cada tentativa é independente das demais.
2) Há apenas dois resultados possíveis em cada tentativa: um de interesse, associado à variável X, chamado de sucesso e o seu complementar que é o fracasso.
3) A probabilidade de sucesso será denotada por p e é a mesma em cada tentativa (entenda Ensaio de Bernoulli). Logo, a probabilidade de fracasso será denotada por q = 1 – p.
Observações importantes: é comum àqueles que estão iniciando os estudos da distribuição Binomial acharem que a variável definida como sucesso precisa ser algo “bom”. Porém, isso não está correto. A variável X, ou seja, o sucesso, deverá ser algo que nos interesse. Por exemplo, poderíamos definir como sucesso:
– alunos reprovados em determinado ano;
– número de óbitos em uma UTI;
– número de fumantes presentes em uma reunião;
– acertar um alvo num torneio de tiro;
– entrevistados serem do sexo masculino;
– sair cara no lançamento de uma moeda;
– sair face 5 ou 6 no lançamento de um dado.
Ou seja, a variável sucesso pode ser ou pode não ser algo bom! Às vezes, pode ser algo imparcial, como face de uma moeda ou dado, ou sexo de uma pessoa.
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
Já vimos que necessitaremos calcular o valor do número binomial que está presente na fórmula da probabilidade da Distribuição Binomial. Esse número binomial nada mais é do que uma combinação de n elementos tomados k a k. Veremos, a seguir, duas formas de calcular esse valor: com e sem calculadora.
Já vimos, no exemplo anterior, que:
No vídeo a seguir, você poderá assistir uma vídeo aula com a explicação do cálculo SEM a utilização de uma calculadora.
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
A grande maioria das calculadoras científicas já possuem uma função que permite o cálculo do valor de uma combinação (ou número binomial).
No vídeo a seguir, você poderá assistir uma vídeo aula com a explicação do cálculo utilizando uma calculadora científica simples da Casio.
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
Para entender melhor a fórmula, vamos recapitular o cálculo de probabilidades com base em um exemplo. Responda rapidamente a pergunta: um casal deseja ter 4 filhos, 2 homens e 2 mulheres. Supondo que a probabilidade de nascimento de um homem (H) ou uma mulher (M) seja a mesma, qual a probabilidade de tal fato acontecer?
Muitas pessoas respondem 50%. Se você foi uma delas, a pergunta seguinte possivelmente será “por quê? Não é???”. A resposta é não! O que mostra que muitas vezes a intuição nos engana, enfatizando a importância da probabilidade (veja, por exemplo, o caso de um médico obstetra ou um laboratório que muitas vezes precisa conhecer cálculos de probabilidades como este).
Faremos, inicialmente, um método mais trabalhoso, mas que certamente convencerá o leitor de que tal probabilidade não é 50%. Depois, faremos o cálculo utilizando um modelo probabilístico.
Listemos todas as possibilidades de nascimentos:
HHHH
HHHM
HHMH
HMHH
MHHH
HHMM
HMHM
MHHM
HMMH
MHMH
MMHH
HMMM
MHMM
MMHM
MMMH
MMMM
Das 16 possibilidades listadas, note que em 6 delas ocorrem o nascimento de 2 homens e 2 mulheres. Logo, a probabilidade de isso ocorrer é:
P = 6/16 = 0,375 ou 37,5%
Ou seja, a probabilidade é inferior a 50%, mais precisamente, vale 37,5%, o que contradiz a intuição da maioria das pessoas.
Uma outra forma de resolver esse mesmo problema é utilizando a Binomial.
Agora, para resolvermos essa situação apresentada através da Binomial, vamos determinar que nosso interesse seja o número de homens que nascem. Essa ocorrência será chamada de sucesso. Assim:
X: número de homens que nascem (sucesso)
Logo, nascer mulher indicaria fracasso. Não é nenhum tipo de preconceito, mas sim, uma questão Estatística. Poderíamos, sem problemas, ter trocado homem por mulher e vice-versa.
A probabilidade de sucesso é a probabilidade de em um nascimento qualquer ocorrer um homem, ou seja, p = 1/2 = 0,5.
Temos interesse que, em 4 nascimentos, 2 sejam homens e 2 sejam mulheres. Como chamamos de sucesso nascer homem, temos interesse no nascimento de 2 homens ou, em linguagem matemática, X=2. Logo, o valor de k é 2 (basta comparar a fórmula X=k com o que acabamos de escrever X=2).
Obtemos, portanto:
que é o mesmo valor obtido utilizando o método anterior.
Cabe ressaltar que a fórmula apresentada não tem caráter místico algum. É possível fazer a sua dedução e, para isso, basta utilizarmos a lógica desenvolvida no método anterior.
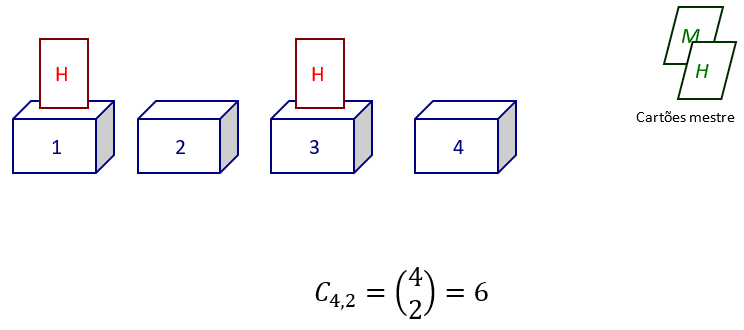
Suponhamos 4 caixas numeradas, e que iremos colocar em cada uma delas um cartão que possui uma letra H ou um cartão que possui uma letra M. Suponhamos que temos um par de cartões “mestre” que serão utilizados na escolha de uma das letras e que tenhamos uma outra pilha de cartões que serão colocados nas caixas.
Inicialmente, escolheremos duas delas para colocarmos um cartão que possui a letra H. O número de maneiras que podemos fazer tal escolha não depende da ordem, ou seja, escolher a caixa 1 e 3 é indiferente de escolher a 3 e 1, visto que colocaremos cartas iguais dentro de cada uma delas. Utilizamos a combinação:
Logo, há 6 maneiras de se fazer tal escolha.
Fixemos uma das escolhas, como por exemplo, H nas caixas 1 e 3. Nas caixas 2 e 4 colocaremos cartas com a letra M. A probabilidade de tal fato ocorrer pode ser expressa através do princípio multiplicativo. A probabilidade de ocorrer cada H é de 0,5 (pois sorteamos as letras a partir dos cartões-mestre) e de ocorrer M também é 0,5.
Assim, a probabilidade de sortearmos H na primeira vez, M na segunda, H na terceira e M na quarta é dada por
0,5.0,5.0,5.0,5 = (0,5)⁴ = 0,0625.
Como tal fato (2 H e 2 M) pode ocorrer de 6 maneiras diferentes temos que a probabilidade final fica
P = 6 . 0,0625 = 0,375.
Note que 0,5 = 1 – 0,5 = 1 – p. O raciocínio aqui desenvolvido é o mesmo que se faz para deduzir a fórmula da Distribuição Binomial.
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
Uma urna tem 4 bolas vermelhas (V) e 6 brancas (B). Uma bola é extraída, observada sua cor e reposta na urna. O experimento é repetido 5 vezes. Qual a probabilidade de observarmos exatamente 3 vezes bola vermelha?
Inicialmente, vamos definir a variável aleatória de interesse:
X: número de bolas vermelhas observadas (sucesso).
Logo, a probabilidade de sucesso será p = 4/10 = 0,4. Utilizando a fórmula apresentada, em que n=5 (número de retiradas) e k=3 (número de bolas vermelhas que temos interesse em observar), temos:
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
Em uma cidade, 10% das pessoas possuem carro de marca A. Se 30 pessoas são selecionadas ao acaso, com reposição, qual a probabilidade de exatamente 5 pessoas possuírem carro de marca A?
Definindo X: número de pessoas que possuem o carro da marca A (sucesso), temos associada uma probabilidade de sucesso p=0,10. Sendo n=30 e k=5, temos:
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
Admite–se que uma válvula eletrônica, instalada em determinado circuito, tenha probabilidade 0,3 de funcionar mais de 600 horas. Analisando–se 10 válvulas, qual será a probabilidade de que, entre elas, pelo menos 3 continuem funcionando após 600 horas?
Seja X: número de válvulas que permanecem funcionando após 600 horas. Temos que a probabilidade de sucesso é p=0,3. Perceba que estamos realizando 10 Ensaios de Bernoulli (n=10). Logo, queremos calcular:
P(X≥3) = P(X=3) + P(X=4) + P(X=5) + ... + P(X=9) + P(X=10).
Note que teríamos que calcular cada uma das probabilidades envolvidas nessa soma utilizando a fórmula apresentada, ou seja, teríamos que aplicar a fórmula 8 vezes para, em seguida, somar todos os resultados. Neste caso, vamos utilizar uma propriedade, já vista, de eventos complementares:
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
Em uma grande pesquisa com 6000 respondentes, determinou–se que 1500 dos entrevistados assistiam determinado programa de TV. Se 20 pessoas são escolhidas ao acaso, qual a probabilidade de que ao menos 19 assistam a esse programa?
Definindo a variável aleatória que indica sucesso:
X: número de pessoas que assistem ao programa.
Perceba que a probabilidade de sucesso (p) pode ser calculada a partir do enunciado:
p = 1500/6000 = 0,25.
Logo, queremos calcular:
P(X≥19) = P(X=19) + P(X=20) =
=5,5.10–11, ou seja, a probabilidade de 19 ou 20 pessoas assistirem ao programa é muito pequena, quase zero, visto que vale 0,0000000055%.
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
Vamos supor o lançamento de uma moeda honesta (ou seja, P(cara)=P(coroa)=0,5). Suponhamos que você faça uma aposta com um amigo seu: ganha aquele que obtiver mais caras (no seu caso) ou coroas (no caso dele) em 7 lançamentos.
A probabilidade de você ganhar ocorre quando saírem 4 ou 5 ou 6 ou 7 caras. Utilizando o modelo Binomial onde:
X: número de caras (sucesso)
n = 7 lançamentos
k = 4,5,6,7
p = 0,5
Obtemos:
P(ganhar) = P(X=4) + P(X=5) + P(X=6) + P(X=7) =
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
Suponhamos a mesma situação do exemplo anterior, mas agora, você pega, sem seu amigo perceber, uma moeda viciada em que a probabilidade de ocorrer uma cara é de 0,75 ou . Neste caso, p=0,75 e a probabilidade de você ganhar é:
P(ganhar) = P(X=4) + P(X=5) + P(X=6) + P(X=7) =
= 0,9294 ou 92,94%.
Logo, é muito provável que você ganhe a aposta usando essa moeda viciada.
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
Overbooking é prática realizada na aviação do mundo todo. Consiste na empresa aérea vender mais bilhetes do que o disponível no voo com base na média de desistência dos voos anteriores. Uma empresa aérea possui um avião com capacidade para 100 lugares. Se para certo voo essa empresa vendeu 103 passagens e, admitindo que a probabilidade de um passageiro não comparecer para embarque é de 1%, qual a probabilidade de algum passageiro não conseguir embarcar?
Este é um problema clássico resolvido utilizando a Binomial. Aqui, é muito comum haver certa confusão na elaboração do que é o sucesso bem como do que se deseja calcular. Assim, vamos definir:
X: número de passageiros que comparecem ao embarque (sucesso).
Neste caso, p=0,99. Temos, ainda, que n=103, visto que cada um dos 103 passageiros pode comparecer ao embarque (sucesso) ou não comparecer (fracasso). Queremos calcular a probabilidade de que algum passageiro não consiga embarcar, ou seja, de que compareçam ao embarque mais de 100 passageiros:
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
Seja uma variável X com distribuição Binomial de parâmetros n (número de ensaios de Bernoulli) e p (probabilidade de sucesso). A média ou valor esperado ou, ainda, esperança de X é dado por:
μ = E(X) = n.p
Nas mesmas suposições da média, temos que a variância pode ser calculada por uma das fórmulas:
σ² = Var(X) = n.p.q
ou
σ² = Var(X) = n.p.(1-p)
Para o cálculo do desvio padrão, basta lembrar que o desvio padrão é igual à raiz quadrada da variância:
ou, ainda,
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
Consideremos o exemplo anterior que trata sobre o Overbooking. Determine a média, variância e desvio padrão para a variável X definida anteriormente. Interprete os resultados.
Lembrando que:
n=103
p=0,99
q=1–0,99=0,01
Então:
E(X) = 103 . 0,99 = 101,97
Var(X) = 103 . 0,99 . 0,01 = 1,0197
Logo, em média comparecem ao embarque aproximadamente 102 (101,97) passageiros com um desvio padrão de 1 passageiro.
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
Em uma determinada cidade, 56% dos dias de um ano possuem tempo limpo e ensolarado. No mês de abril, quantos dias espera-se que tenham tempo limpo e ensolarado?
Vamos considerar a variável aleatória X como representando o número de dias com tempo limpo e ensolarado. No mês de março há 30 dias. Então:
n = 30
p = 0,56
Logo:
E(X) = n.p = 30 . 0,56 = 16,8.
Portanto, esperamos que em aproximadamente 17 dias do mês de março haja tempo limpo e ensolarado.
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
Em uma pesquisa realizada verificou-se que três a cada oito pessoas tem dificuldades para pegar no sono. Uma amostra aleatória de 25 pessoas é selecionada. Determine a média e o desvio padrão do número de pessoas que possuem dificuldades para pegar no sono dentro dessa amostra.
Definindo:
X: número de pessoas que tem dificuldade para pegar no sono
Temos do enunciado:
n = 25
p = 3/8 = 0,375
E(X) = n.p = 25 . 0,375 = 9,375
Var(X) = n.p.(1-p) = 25 . 0,375 . (1-0,375) = 5,8594
O desvio padrão será a raiz quadrada da variância e, portanto:
DP(X) = 2,42
Logo, nessa amostra, esperamos encontrar, aproximadamente, 9 pessoas com dificuldades de pegar no sono.
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
1) Uma moeda é lançada 6 vezes. Qual a probabilidade de observarmos exatamente duas caras?
2) Um dado é lançado 5 vezes. Qual a probabilidade de que o “4” apareça exatamente 3 vezes?
3) Uma pessoa tem probabilidade 0,2 de acertar num alvo toda vez que atira. Supondo que as vezes que ela atira são ensaios independentes, qual a probabilidade de ela acertar no alvo exatamente 4 vezes, se ela dá 8 tiros?
4) A probabilidade de que um homem de 45 anos sobreviva mais 20 anos é 0,6. De um grupo de 5 homens com 45 anos, qual a probabilidade de que exatamente 4 cheguem aos 65 anos?
5) Uma moeda é lançada 6 vezes. Qual a probabilidade de observarmos ao menos uma cara?
6) Um time de futebol tem probabilidade p = 0,6 de vencer todas as vezes que joga. Se disputar 5 partidas, qual a probabilidade de que vença ao menos uma?
7) Uma prova consta de 5 testes com 4 alternativas cada um, sendo apenas uma delas correta. Um aluno que nada sabe a respeito da matéria da prova, “chuta” uma resposta para cada teste. Qual é a probabilidade desse aluno:
a) acertar os 5 testes?
b) acertar apenas 4 testes?
c) acertar apenas 3 testes?
d) acertar apenas 2 testes?
e) acertar apenas 1 teste?
f) errar todos os testes propostos?
g) qual o resultado mais provável obtido pelo aluno?
8) Foi realizada uma pesquisa com 500 pessoas para verificar se assistiam determinado programa de televisão. Duzentas pessoas afirmaram assistir. Se, a partir da população, retirarmos 8 indivíduos, qual é a probabilidade de que no máximo 6 assistam o programa?
9) Um aluno tem 70% de chance de acertar cada questão de uma prova. Sabendo–se que essa prova é composta por 10 questões, qual a probabilidade de ele acertar, ao menos, 7 questões para ser aprovado?
10) Em uma UTI, em média 5% dos bebês que nascem prematuros não sobrevivem. Se, atualmente, há 40 bebês prematuros, qual a probabilidade de que no máximo 5% dos bebês não sobrevivam?
11) Em 320 famílias com quatro crianças cada uma, quantas famílias seriam esperadas que tivessem:
a) nenhuma menina?
b) três meninos?
c) quatro meninos?
12) Um time X tem 2/3 de probabilidade de vitória sempre que joga. Se X jogar cinco partidas, calcule a probabilidade de:
a) X vencer exatamente três partidas;
b) X vencer ao menos uma partida;
c) X vencer mais da metade das partidas.
13) A probabilidade de um atirador acertar o alvo é 1/3. Se ele atirar seis vezes, qual a probabilidade de:
a) acertar exatamente dois tiros?
b) não acertar o alvo?
c) acertar o alvo?
d) acertar ao menos 1 tiro no alvo?
14) Se 5% das lâmpadas de certa marca são defeituosas, ache a probabilidade de que, numa amostra de 100 lâmpadas, escolhidas ao acaso, tenhamos:
a) nenhuma defeituosa;
b) três defeituosas;
c) mais do que uma boa.
15) Um dado é lançado 5 vezes. Qual a probabilidade de que a face “2” apareça pelo menos uma vez nos 5 lançamentos?
1) 0,2344
2) 0,03215
3) 0,0459
4) 0,2592
5) 0,98439
6) 0,9898
7) a) 1/1024 b) 15/1024 c) 90/1024 d) 270/1024 e) 405/1024 f) 243/1024
g) O resultado mais provável é que o aluno acerte apenas 1 teste.
8) 0,9915
9) 0,6496
10) 0,6767
11) a) 20 b) 80 c) 20
12) a) 80/243 b) 242/243 c) 64/81
13) a) 0,3292 b) 0,0878 c) 0,9122 d) 0,9122
14)
15) 4651/7776 = 0,5981
Faça o download gratuito da apostila sobre Distribuição Binomial em formato PDF.
Baixe AgoraVocê também pode se interessar por:
Fatorial, Princípio Fundamental da Contagem (PFC), Permutação simples, Permutação com repetição, Arranjo e Combinação
Conceitos e fórmulas da distribuição de Poisson, probabilidade, esperança, variância, desvio padrão, exemplos resolvidos e lista de exercícios
Conceitos e propriedades da distribuição Normal, padronização, distribuição Normal Padrão, tabela da Normal Padrão, exemplos resolvidos e lista de exercícios