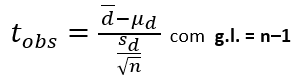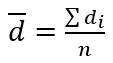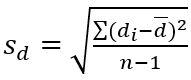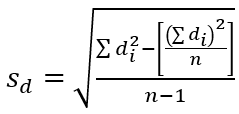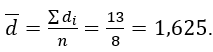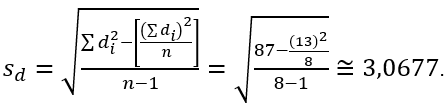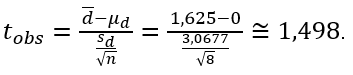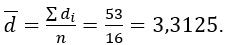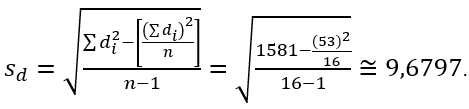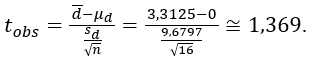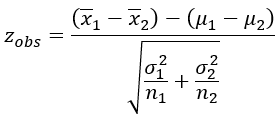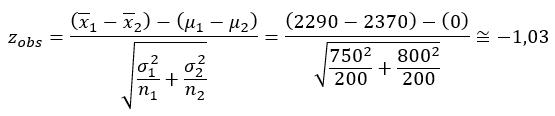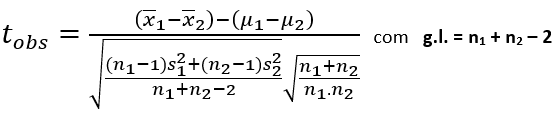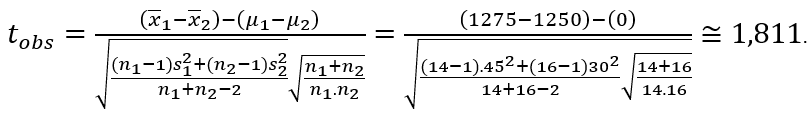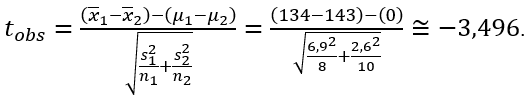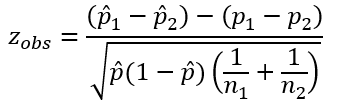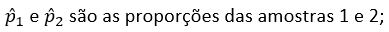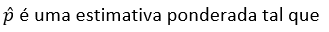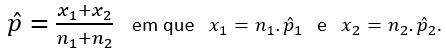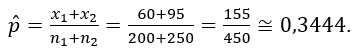1. Introdução

Neste capítulo veremos como fazer testes de hipóteses para a média populacional e para a proporção não para uma única população, mas para comparar duas populações e verificar se existem diferenças significativas entre elas.

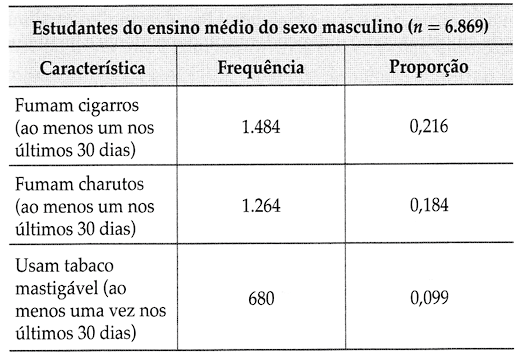
A National Youth Tobacco Survey (NYTS) é um estudo conduzido pelo Centers for Disease Control and Prevention (Centro para Prevenção e Controle de Doenças) para fornecer informações sobre o uso de produtos derivados de tabaco por estudantes. Como parte de um estudo recente, uma amostra aleatória de 6.869 estudantes do ensino médio do sexo masculino foi pesquisada. As proporções a seguir foram encontradas.

Neste capítulo, você continuará seu estudo sobre estatística inferencial e teste de hipóteses. Agora, no entanto, ao invés de testar uma hipótese sobre uma única população, você aprenderá como testar uma hipótese que compara duas populações.

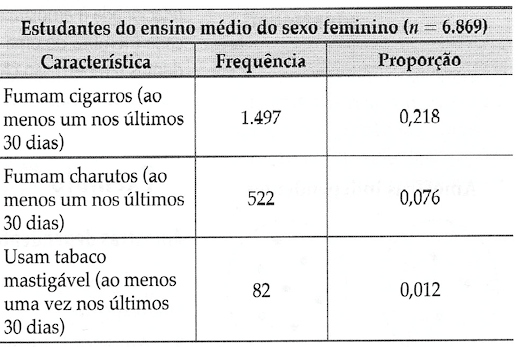
Por exemplo, no estudo da NYTS, uma amostra aleatória de 6.869 estudantes do ensino médio do sexo feminino também foi pesquisada. Aqui estão as conclusões para esse segundo grupo.

Com base nestas duas amostras, você pode concluir que existe uma proporção significativamente maior de estudantes que fumam cigarros, charutos ou usam tabaco mastigável entre estudantes do sexo masculino do que entre estudantes do sexo feminino? Ou as diferenças nas proporções podem ser ao acaso?

Neste capítulo, você aprenderá que pode responder a essas perguntas testando a hipótese de que as duas proporções são iguais. Para a proporção dos estudantes que usam tabaco mastigável, por exemplo, o P–valor para a hipótese de que p1=p2 é de cerca de 0,0000. Então, é quase impossível que dois grupos que usam tabaco mastigável tenham experimentado a mesma proporção.

2. Amostras dependentes e independentes

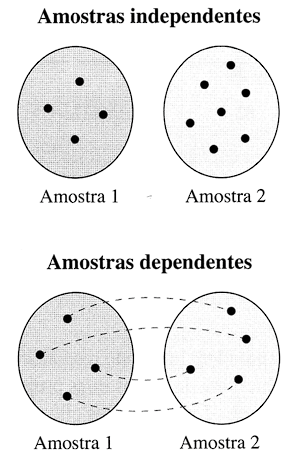
Duas amostras são independentes se a amostra selecionada de uma das populações não é relacionada à amostra selecionada da segunda população.

Duas amostras são dependentes se cada membro de uma amostra corresponde a um membro da outra amostra. Amostras dependentes também são chamadas de amostras emparelhadas ou amostras relacionadas.

Exemplo 1

Classifique cada par de amostras como independente ou dependente e justifique sua resposta.

a) Amostra 1: ritmo cardíaco em descanso de 35 indivíduos antes de tomar café.

Amostra 2: ritmo cardíaco em descanso dos mesmos indivíduos depois de beber duas xícaras de café.

b) Amostra 1: nota de teste para 35 estudantes de Estatística.

Amostra 2: nota de teste para 42 estudantes de Biologia que não estudam Estatística.

Resolução

a) As amostras são dependentes. Já que o ritmo cardíaco em descanso dos mesmos indivíduos é analisado, as amostras são relacionadas. As amostras podem ser emparelhadas em relação a cada indivíduo.

b) As amostras são independentes. Não é possível formar uma relação entre os membros das amostras; os tamanhos das amostras são diferentes e os dados representam notas de teste para diferentes indivíduos.

Exemplo 2

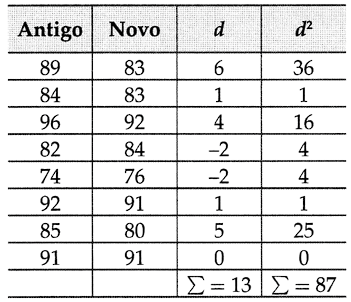
Um fabricante de tacos de golfe afirma que os golfistas podem diminuir seus placares usando os tacos de golfe recém-projetados por ele. Oito jogadores de golfe são escolhidos aleatoriamente e é pedido a cada um que forneça seu mais recente placar. Após usar os novos tacos por um mês, é pedido novamente aos jogadores que forneçam seus placares mais recentes. Os placares para cada um são mostrados na tabela. Assumindo que os placares de golfe são distribuídos normalmente, existe evidência suficiente para apoiar a afirmação do fabricante para um nível de significância de 10%?

Resolução

A afirmação é que "golfistas podem diminuir seus placares". Em outras palavras, o fabricante afirma que os placares, usando os tacos antigos, será maior do que os placares usando os novos. Observação: no golfe, quanto menor for o placar, melhor é o desempenho do jogador. Cada diferença é dada por:

d = (placar antigo) – (placar novo).

As hipóteses são:

H₀: μd ≤ 0

Hₐ: μd > 0 (afirmação).

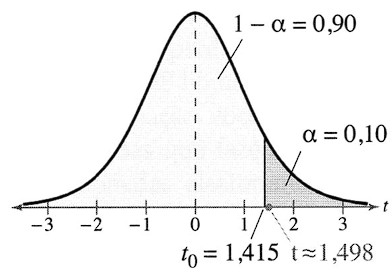
Já que o teste é um teste unicaudal à direita, α=0,10 e g.l. = 8 – 1 = 7, o valor crítico, obtido a partir da tabela t é tc=1,415. A área de rejeição (região crítica do teste) é t>1,415. Usando a tabela a seguir, você pode calcular a média das diferenças e o desvio padrão das diferenças. Note que a fórmula de “atalho” é usada para calcular o desvio padrão.

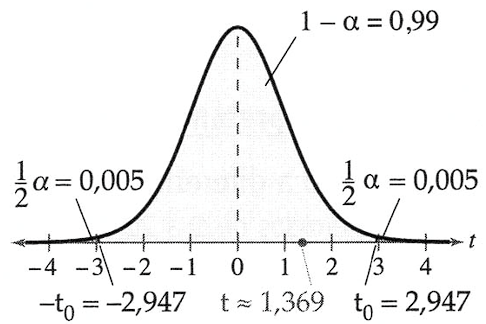
O gráfico mostra a localização da região de rejeição (região crítica do teste) e a estatística tobs.

Exemplo 3

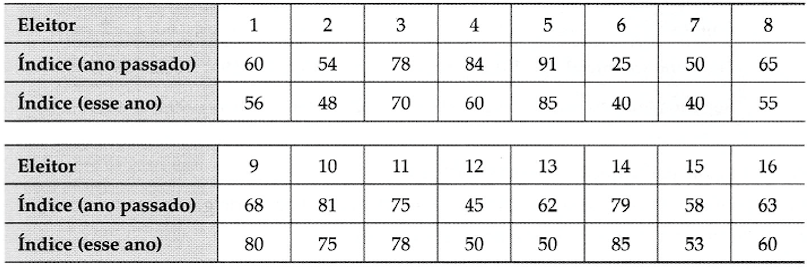
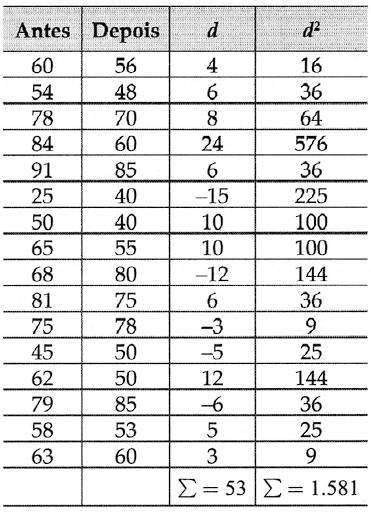
Um legislador estadual quer determinar se seu índice de desempenho (0-100) mudou do ano passado para este. A tabela a seguir mostra o índice de desempenho do legislador para 16 eleitores selecionados aleatoriamente para o ano passado e para este. Ao nível de 1% de significância, há evidência suficiente para concluir que o desempenho do legislador mudou? Assuma que os índices de desempenho são normalmente distribuídos.

4. Teste para Médias de Amostras Independentes com Variâncias Populacionais Conhecidas

Neste teste, iremos verificar se existem diferenças significativas nas médias de duas populações. As amostras, de cada uma das populações, devem ser independentes e serem selecionadas aleatoriamente. Além disso, as variâncias, e consequentemente, os desvios padrões populacionais devem ser conhecidos.

A estatística padronizada do teste é uma Normal Padrão. Sendo assim, a fórmula para o teste de médias de amostras independentes com variâncias conhecidas é:

5. Teste para Médias de Amostras Independentes com Variâncias Populacionais Desconhecidas e Iguais

Se as amostras forem independentes, aleatórias e tiverem uma distribuição normal, em que as variâncias populacionais são iguais, porém desconhecidas, a fórmula do teste de hipóteses é:

Os graus de liberdade são: g.l.=14+16–2=28 . Logo, a partir da distribuição t-Student, para 5% de significância, obtemos o valor crítico (teste unicaudal): tc=1,701.

Logo, como o valor observado pertence à região crítica do teste, devemos rejeitar H₀, ou seja, ao nível de 5%, há evidências de que o alcance de chamada do fabricante é maior do que o alcance do seu concorrente.

6. Teste para Médias de Amostras Independentes com Variâncias Populacionais Desconhecidas e Diferentes

Se as amostras forem independentes, aleatórias e tiverem uma distribuição normal, em que as variâncias populacionais são diferentes e desconhecidas, a fórmula do teste de hipóteses é:

7. Teste para a igualdade de Proporções

Um teste Z de duas amostras é usado para testar a diferença entre duas proporções de populações p1 e p2, quando uma amostra é selecionada aleatoriamente de cada população. A fórmula do teste de hipótestes para a igualdade de proporções é:

p1 e p2 são as proporções populacionais das populações 1 e 2;

n1 e n2 são os tamanhos das amostras 1 e 2;

3) Para verificar se duas populações têm a mesma média, amostras independentes foram retiradas. Sabendo que a população I é Normal (µ1,25) e a população II Normal (µ2,40), que conclusão pode ser tirada, ao nível 2%? Os valores obtidos foram:

População                          Dados

       I                   12    14    15    14    13    17    14    13

       II                 13    17    14    13    16    17    18    16

4) Para comparar as médias de duas populações Normais, amostras aleatórias foram obtidas. Sabe-se que as variâncias populacionais são diferentes, sendo seus valores desconhecidos.

Amostra I    7    9    3     8     11     5     9

Amostra II   2    7    5    15     9     16    8

O que pode ser dito a respeito das médias das populações, com α = 0,05?

5) Dois medicamentos para tratamento de infecções bucais estão sendo estudados e o melhor desempenho é definido pela rapidez em eliminar a infecção. Pacientes escolhidos ao acaso receberam um dos medicamentos e tiveram a sua cura classificada em rápida ou não. Deseja-se testar, ao nível 10%, se os medicamentos são equivalentes. Os dados obtidos são apresentados a seguir.

Qual seria sua conclusão? Indique as hipóteses do teste e as suposições necessárias.

6) Uma empresa de pesquisa de opinião pública seleciona 300 eleitores de São Paulo e 400 do Rio de Janeiro, e pergunta a cada um se votará ou não no candidato A, nas próximas eleições. Setenta e cinco eleitores de SP e 120 do RJ respondem afirmativamente. Há diferença significativa entre as proporções de eleitores a favor de A nos dois estados? Use nível de significância de 5%.

7) Estão em teste dois processos para fechar latas de comestíveis. Em uma sequência de 1.000 latas, o processo l gera 50 rejeições, enquanto o processo 2 acusa 200 rejeições. Podemos, no nível de 0,05, concluir que os dois processos sejam diferentes?

8) Em uma pesquisa sobre possuidores de videocassete, encontram-se 120 das 200 casas pesquisadas do bairro X e 240 das 500 residências do bairro Y. Há diferença significativa entre a proporção de possuidores de vídeo nos dois bairros a um nível de 10%?

9) Você quer comprar um forno de micro-ondas e escolherá o Modelo A se os custos de reparo forem mais baixos que os custos de reparo do Modelo B. Você pesquisa os custos de reparo de 47 fornos do Modelo A e 55 fornos do Modelo B. O custo médio do reparo do modelo A é $ 75 e, do modelo B, $ 80. Ao nível de 1%, você compraria o Modelo A? Considere que o desvio padrão populacional para o modelo A é $ 12,50 e para o modelo B é $ 20.

10) Da população feminina extraiu–se uma amostra, resultando:

Da população feminina extraiu–se uma amostra, resultando:

Admitindo que as populações tenham distribuições Normais de mesma variância para os salários, teste, ao nível de 10%, a hipótese de que a diferença entre a renda média dos homens e das mulheres valha $5000.

11) A média na nota do ACT para 43 estudantes do sexo masculino do ensino médio é de 21,1. A média na nota do ACT para 56 estudantes do sexo feminino do ensino médio é de 20,. Os desvio padrão, obtido a partir de vários estudos anteriores, é de 5,0 para o sexo masculino e de 4,7 para o sexo feminino. Ao nível de 1%, você pode rejeitar a afirmação de que estudantes do ensino médio do sexo masculino e do sexo feminino têm a mesma média de notas do ACT?

12) Intrusão do footwell (compartimento na parte frontal do carro, cuja função é acomodar os pés) Um atuário de seguros afirma que a média de intrusões de footwell para carros pequenos e médios é igual. Testes de impacto a 40 milhas por hora foram realizados em 12 carros pequenos selecionados aleatoriamente e em 17 carros médios selecionados aleatoriamente. A quantia média que o footwell irrompe nas pernas do motorista foi medida. A média de intrusão do footwell nos carros pequenos foi de 10,1 cm com desvio padrão de 4,11 cm. Para os carros médios foi de 8,3 cm com desvio padrão de 4,02 cm. Ao nível de 10%, você pode rejeitar a afirmação? Assuma que as variâncias populacionais sejam iguais.

13) Em testes de batida a 5 milhas por hora, a média do custo de reparo no para-choque de 14 carros pequenos selecionados aleatoriamente é $ 473 com um desvio padrão de $ 190. Em testes similares de 23 carros de tamanho médio selecionados aleatoriamente, a média do custo de reparo no para-choque é $ 741 com um desvio padrão de $ 205. Você pode concluir que a média do custo de reparo no para-choque é menor em carros pequenos do que em carros de tamanho médio ao nível de 10%? Assuma que as variâncias de população são iguais.

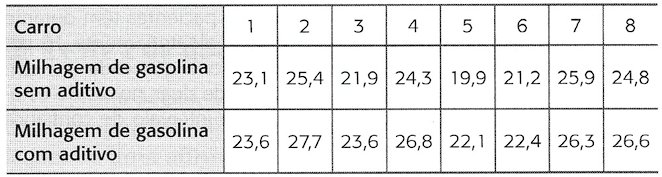
14) A tabela mostra as milhagens de gasolina (em milhas por galão) de oito carros com e sem uso de um aditivo de combustível. Ao nível de 10%, há evidência suficiente para concluir que o aditivo de combustível melhorou a milhagem de gasolina?

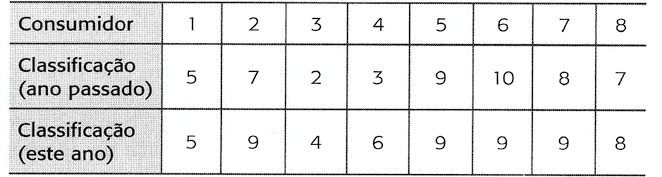
15) Uma empresa quer determinar se a classificação de seus produtos por consumidores (0-10) mudou do ano passado para este ano. A tabela mostra a classificação dos produtos da empresa feita pelos mesmos oito consumidores do ano passado para este ano. Ao nível de 5% de significância, há evidência suficiente para concluir que a classificação do produto mudou?

16) Em um estudo de 1.539 adultos em 1991, 520 disseram que tinham usado medicina alternativa (por exemplo, remédios populares e homeopatia) no ano anterior. Em um estudo mais recente com 2.055 adultos, 865 disseram que haviam usado medicina alternativa no ano anterior (veja o gráfico). Ao nível de 5%, você pode rejeitar a afirmação de que a proporção de adultos usando medicina alternativa não mudou desde 1991?

17) Em uma pesquisa com 5.240 cidadãos mais velhos do sexo masculino, 2.201 disseram que comem o número de porções recomendadas de vegetais diariamente. Em uma pesquisa com 6.180 cidadãs mais velhas, 2.348 disseram que também comem o número de porções recomendadas de vegetais diariamente. Com 10% de significância, você pode rejeitar a afirmação de que as proporções de cidadãos mais velhos que disseram comer o número de porções recomendadas de vegetais diariamente são as mesmas para os dois grupos?

18) Fumantes: homem e mulher. Em uma pesquisa de 9.300 homens, 2.083 disseram que haviam fumado nos últimos 30 dias. Em uma pesquisa de 4.900 mulheres, 985 disseram que haviam fumado nos últimos 30 dias. Ao nível de 1%, você pode apoiar a afirmação de que a proporção de homens que disseram ter fumado nos últimos 30 dias é menor do que a proporção de mulheres que disseram ter feito o mesmo?