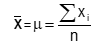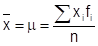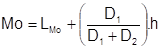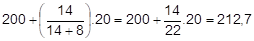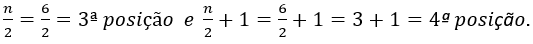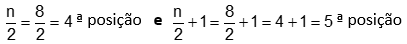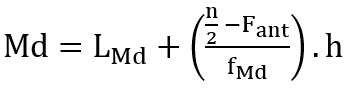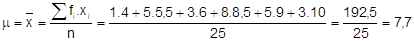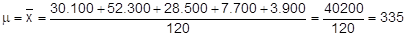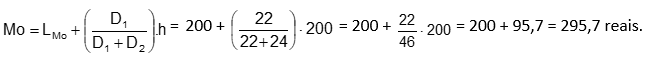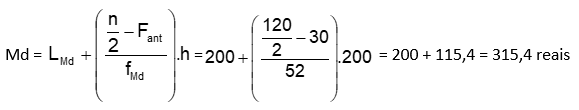Conrad Elber Pinheiro
Professor Guru
Atualizado em 10/07/2023
Introdução
1. Média
Média - Caso I: Dados não agrupados
Média - Caso II: Dados agrupados sem intervalos de classe
Média - Caso III: Dados agrupados com intervalos de classe
2. Moda (Mo)
Moda - Caso I: Dados não agrupados
Moda - Caso II: Dados agrupados sem intervalos de classe
Moda - Caso III: Dados agrupados com intervalos de classe
3. Mediana (Md)
Mediana - Caso I: Dados não agrupados
Mediana- Caso II: Dados agrupados sem intervalos de classe
Mediana - Caso III: Dados agrupados com intervalos de classe
4. Exemplos resolvidos: média, moda e mediana
5. A média é representativa?
6. Lista de Exercícios
Respostas dos Exercícios
Ao final desta página, você pode fazer o download gratuito da apostila sobre Medidas de Posição em formato PDF.
Clique aqui para assistir a playlist com os conteúdos desta página no YouTube
Depois de se fazer a coleta e a representação dos dados de uma pesquisa, é comum analisarmos as tendências que essa pesquisa revela. Assim se a pesquisa envolve muitos dados, convêm sintetizarmos todas essas informações a um mínimo de parâmetros que possam caracterizá-la. Esses parâmetros podem ser de:
- centralização: média aritmética, mediana e moda.
- separatrizes: mediana, quartis e percentis.
E também, utilizamos as medidas de dispersão que serão vistas posteriormente: intervalo de variação, desvio médio, variância e desvio padrão.
A média caracteriza o centro da distribuição de frequências, sendo, por isso uma medida de posição. Podemos definir vários tipos de médias de um conjunto de dados, temos a média aritmética, a média geométrica, a média harmônica, etc.
Aqui, trabalharemos exclusivamente com a média aritmética (simples ou ponderada).
É comum distinguirmos, em termos de notação, a média amostral e a média populacional, embora o cálculo de ambas seja o mesmo e apresente, portanto, o mesmo resultado. As notações para a média populacional e média amostral são:
Há três formas para calcular a média. Isso depende de como está o nosso conjunto de dados: não agrupados, agrupados sem classes ou agrupados com classes.
Importante
Nunca devemos arredondar o valor da média, mesmo que esse número não faça, aparentemente, sentido. Por exemplo: se calculamos que o número médio de filhos é 1,8, não devemos arredondar para 2. Embora não faça sentido falarmos em 1,8 filhos por família, pense em 18 filhos (em média) a cada 10 famílias, ou, ainda, 180 filhos, em média, a cada 100 famílias. Agora, o número médio passa a ter um sentido “prático”.
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
Para uma sequência numérica X: x1, x2, …, xn, a média aritmética simples, tanto amostral quanto populacional, é definida por:
Calcular a média da série X : 2, 0, 5, 3.
Aplicando a fórmula:
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
Se os dados estão apresentados na forma de uma variável discreta faremos a média aritmética ponderada considerando as frequências simples de fi como sendo as ponderações dos elementos xi correspondentes:
Assim a fórmula para o cálculo da média é:
Considerando a distribuição:
|
xi |
fi |
|
2 |
1 |
|
4 |
3 |
|
5 |
2 |
|
total |
6 |
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
Quando os dados estão agrupados com intervalos de classes, ou seja, quando se trata de uma variável contínua, se aceita, por convenção, que as frequências se distribuem uniformemente ao longo da classe e que, portanto, o ponto médio da classe é o valor representativo do conjunto. Neste caso a média será calculada fazendo a média aritmética ponderada considerando as frequências simples de fi como sendo as ponderações dos elementos correspondentes, onde x i é o ponto médio do intervalo. Assim, a fórmula para o cálculo da média é a mesma que a do caso II:
Considere a distribuição:
|
classe |
fi |
xi |
|
180 |― 200 |
4 |
190 |
|
200 |― 220 |
18 |
210 |
|
220 |― 240 |
10 |
230 |
|
240 |― 260 |
5 |
250 |
|
260 |― 280 |
3 |
270 |
|
total |
40 |
--- |
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
A moda de uma série de valores é o valor de maior frequência absoluta, ou seja, o valor que aparece o maior número de vezes na distribuição. Fique atento: moda é um valor, ou seja, x i . Moda NÃO é a frequência (f i )!
Assim como no caso da média, vamos considerar três casos para obtermos a moda.
Dada a série: 2, 0, 0, 5, 3, observamos que o valor 0 ocorreu duas vezes. Logo, Mo = 0. Neste caso, o conjunto é chamado de unimodal.
Seja o ROL: 1, 2, 5, 7, 12,18, notamos que não existe um valor que apareça mais vezes. Neste caso, dizemos que a série de dados é amodal (não há moda).
Dada a série: 1, 1, 2, 2, 2, 3, 3, 3, 4, 5, 5, 6, vemos que os valores 2 e 3 ocorreram três vezes cada um. Neste caso, temos dois valores modais, ou seja, Mo = 2 e 3. A série é dita bimodal.
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
Considerando a distribuição:
|
xi |
fi |
|
2 |
1 |
|
4 |
3 |
|
5 |
2 |
|
total |
6 |
A maior frequência é 3, que corresponde ao valor 4. Logo, Mo = 4.
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
Neste caso, a classe que apresenta a maior frequência é denominada classe modal. No caso de distribuição de frequências em classes de mesma amplitude, a moda corresponde a um ponto pertencente à classe modal dado pela fórmula de Czuber:
com
D 1 = f Mo – f ant
D 2 = f Mo – f post
em que:
LMo = limite inferior da classe modal
fMo = frequência absoluta da classe modal
fant = frequência absoluta da classe imediatamente anterior à classe modal
fpost = frequência absoluta da classe imediatamente posterior à classe modal
h = amplitude da classe modal
Exemplo
Considere a distribuição:
|
classe |
fi |
x i |
|
180 |― 200 |
4 |
190 |
|
200 |― 220 |
18 |
210 |
|
220 |― 240 |
10 |
230 |
|
240 |― 260 |
5 |
250 |
|
260 |― 280 |
3 |
270 |
|
total |
40 |
--- |
Inicialmente, devemos localizar a CLASSE MODAL, ou seja, a classe que conterá a moda. Ela corresponde ao intervalo que possui maior frequência. No caso: 200 |― 220. Feito isso, basta aplicarmos a fórmula de Czuber:
LMo = 200
fMo = 18
fant = 4
fpost = 10
h = 220-200 = 20
Logo:
D1 = 18 – 4 = 14
D2 = 18 – 10 = 8
A moda será:
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
A mediana de um conjunto de valores, colocados em rol, é o valor situado de tal forma no conjunto que o separa em dois subconjuntos de mesmo número de elementos (elemento que ocupa a posição central). Em outras palavras, tendo-se um conjunto de dados ordenados de maneira crescente (ROL), a mediana é o valor que separa os 50% dos menores dados dos 50% maiores.
Sejam os resultados de 5 lançamentos de um dado: 2, 4, 4, 5, 6. A mediana corresponde ao valor 4, visto que ele é o valor central, deixando 2 dados à sua esquerda e 2 à sua direita. Assim, Md = 4.
Note que n=5 (ímpar). A posição ocupada pela mediana é a 3ª. Essa posição poderia ser obtida da seguinte forma:
Ou seja, a mediana ocupa a 3ª posição que corresponde ao valor Md=4.
Sejam as idades de 9 pessoas: 37, 28, 40, 41, 45, 37, 37, 41, 44.
Colocando os dados em rol temos: 28, 37, 37, 37, 40, 41, 41, 44, 45.
A mediana corresponde ao valor 40 (ou seja, idade), pois há quatro valores à esquerda de 40 e quatro valores à direita de 40. Assim, Md=40.
Perceba que a posição ocupada pela mediana é a 5ª. Utilizando o mesmo raciocínio do exemplo anterior, podemos obter essa posição através do seguinte cálculo:
Logo, a mediana ocupa a 5ª posição que corresponde ao valor Md=40.
Considere o número de filhos de 6 famílias: 0, 0, 1, 2, 3, 3. Perceba que a mediana não poderia ser 1, pois deixaria dois valores à esquerda e três à direita. Da mesma forma, a mediana não poderia ser 2, pois deixaria três valores à esquerda e dois valores à direita. Dessa forma, a mediana será a média aritmética dos dois valores centrais:
(NUNCA arredondar o valor da mediana!)
Observe que a mediana corresponde à média dos valores que ocupam a 3ª e 4ª posições. Essas posições podem ser obtidas da seguinte forma:
Novamente, vamos ressaltar: a 3ª posição é ocupada pelo valor 1; a 4ª posição é ocupada pelo valor 2. A mediana é, portanto, a média aritmética desses valores, ou seja, é o valor 1,5.
Sejam as idades de 8 pessoas: 21, 24, 28, 31, 34, 35, 38, 38
A mediana corresponde a média aritmética dos dois valores centrais, que são 31 e 34. Assim:
Note que o valor 31 anos está na 4ª posição e o valor 34 anos ocupa a 5ª posição. Vamos obter essas posições utilizando a mesma fórmula do exemplo anterior:
Logo, a mediana corresponderá à média dos valores que ocupam as posições (centrais) calculadas.
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
Para determinarmos à mediana de uma distribuição de dados discreta, vamos trabalhar com as situações de n par ou n ímpar que citamos nos exemplos do caso I. Para facilitar a localização da posição da mediana, utilizaremos a frequência acumulada.
Considerando a distribuição:
|
idades |
fi |
Fi |
Significado de Fi (posições) |
|
12 |
3 |
3 |
1ª a 3ª |
|
14 |
5 |
8 |
4ª a 8ª |
|
15 |
6 |
14 |
9ª a 14ª |
|
16 |
2 |
16 |
15ª a 16ª |
|
17 |
5 |
21 |
17ª a 21ª |
|
total |
21 |
--- |
--- |
Inicialmente, calculamos a posição ocupada pela mediana utilizando a regra de n ímpar:
21 / 2 + 0,5 = 10,5 + 0,5 = 11ª posição.
Na tabela, localizamos a linha que contém a 11ª posição, que no caso é a terceira linha. Verificamos o valor que está nessa linha, que no caso é a idade 15. Assim, Md = 15 anos.
Considere a distribuição:
|
idades |
fi |
Fi |
Significado de Fi (posições) |
|
20 |
2 |
2 |
1ª a 2ª |
|
21 |
5 |
7 |
3ª a 7ª |
|
22 |
7 |
14 |
8ª a 14ª |
|
total |
14 |
--- |
--- |
Calculando a posição da mediana, utilizando a regra de n PAR:
14 / 2 = 7ª posição e a seguinte, ou seja, 8ª posição.
Ou seja, os valores centrais da distribuição ocupam a 7ª e 8ª posições.
Na tabela, vemos que a 7ª posição é ocupada pelo valor (idade) 21 anos, enquanto que a 8ª posição é ocupada pelo valor 22 anos. A mediana da distribuição será:
Md = (21 + 22) / 2 = 21,5 anos.
Mais uma vez, perceba que a mediana é um valor. As posições são calculadas apenas para que cheguemos a esse valor, que no caso é Md=21,5.
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
Quando estamos trabalhando com variáveis contínuas, ou seja, quando os dados estão agrupados em classes, determinamos a classe na qual se encontra a mediana, que chamaremos de classe mediana. Neste caso, não nos preocuparemos se estamos trabalhando com uma quantidade de dados par ou ímpar, visto que apenas precisamos determinar a classe que contém a mediana. Em seguida, calculamos o valor da mediana através da fórmula:
em que:
LMd é o limite inferior da classe mediana;
Fant é a frequência acumulada da classe anterior à classe mediana;
h é a amplitude do intervalo da classe mediana;
fMd é a frequência simples (ou absoluta) da classe mediana.
Considere a distribuição:
|
classe |
fi |
F i |
Significado de Fi (posições) |
|
180 |― 200 |
4 |
4 |
1ª a 4ª |
|
200 |― 220 |
18 |
22 |
5ª a 22ª |
|
220 |― 240 |
10 |
32 |
23ª a 32ª |
|
240 |― 260 |
5 |
37 |
33ª a 37ª |
|
260 |― 280 |
3 |
40 |
38ª a 40ª |
|
total |
40 |
--- |
--- |
Vamos verificar qual a classe que contém a mediana. Para isto, vamos calcular a posição ocupada pela mediana:
40 / 2 = 20ª posição.
Note que essa posição corresponde à classe 200 |― 220. Esta é a classe mediana. Utilizando a fórmula apresentada:
LMd = 200
Fant = 4
h= 220 – 200 = 20
fMd = 18
Considerando a distribuição:
|
Alturas (cm) |
fi |
Fi |
Significado de Fi (posições) |
|
150 |― 154 |
4 |
4 |
1ª a 4ª |
|
154 |― 158 |
9 |
13 |
5ª a 13ª |
|
158 |― 162 |
11 |
24 |
14ª a 24ª |
|
162 |― 166 |
8 |
32 |
25ª a 32ª |
|
166 |― 170 |
5 |
37 |
33ª a 37ª |
|
170 |― 174 |
4 |
41 |
38ª a 41ª |
|
total |
41 |
--- |
--- |
Cálculo da classe mediana: 41 / 2 = 20,5ª posição. Vamos arredondar para a 21ª posição. Na tabela, identificamos que essa posição se encontra na classe 158 |― 162. Usando a fórmula:
LMd = 158
Fant = 13
h = 162 – 158 = 4
fMd = 11
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
Vamos obter a média, a moda e a mediana para os casos a seguir.
Considere as notas obtidas por 25 alunos, numa avaliação de Estatística, distribuídas na tabela abaixo. Determine a média, a mediana e a moda.
|
Nota |
fi |
Fi |
|
4 |
1 |
1 |
|
5,5 |
5 |
6 |
|
6 |
3 |
9 |
|
8,5 |
8 |
17 |
|
9 |
5 |
22 |
|
10 |
3 |
25 |
|
Total |
25 |
--- |
Média:
Moda: é o valor com maior frequência. Na tabela, vemos que a maior frequência é 8 e corresponde à nota 8,5. Logo, Mo = 8,5.
Mediana: inicialmente, calculamos a posição da mediana usando a regra do n ÍMPAR:
25/2 + 0,5 = 12,5 + 0,5 = 13ª posição. Utilizando a coluna da frequência acumulada, percebemos que o valor que ocupa a 13ª posição é a nota 8,5. Assim, Md = 8,5.
Resumindo: a nota média obtida na prova feita pelos 25 alunos é 7,7, sendo que a nota 8,5 ocorreu com a maior frequência (moda) e 8,5 é a nota que separa as 50% menores notas obtidas das 50% maiores (mediana).
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
A tabela abaixo indica o aluguel de um grupo de casas.
|
Classe |
Aluguel (R$) |
Nº de casas |
Fi |
xi (ponto médio) |
|
1 |
0 |― 200 |
30 |
30 |
100 |
|
2 |
200 |― 400 |
52 |
82 |
300 |
|
3 |
400 |― 600 |
28 |
110 |
500 |
|
4 |
600 |― 800 |
7 |
117 |
700 |
|
5 |
800 |― 1.000 |
3 |
120 |
900 |
|
|
total |
120 |
--- |
--- |
Média: para o cálculo da média, construímos, na tabela, a coluna do ponto médio, que corresponderá ao nosso xi. Aplicando a fórmula:
Moda: observando as frequências absolutas, percebemos que a segunda classe é aquela que possui a maior frequência, ou seja, a classe modal é 200 |― 400.
Calculamos as diferenças:
D1 = fMo – fant = 52 – 30 = 22
D2 = fMo – fpost = 52 – 28 = 24
Aplicando a fórmula de Czuber:
Mediana: inicialmente, calculamos a posição da mediana para, em seguida, determinar a classe mediana.
120 / 2 = 60ª posição
Esta posição está na segunda classe, ou seja, na classe 200 |― 400 (classe mediana).
Logo:
LMd = 200
Fant = 30
h= 400 – 200 = 200
fMd = 52
Aplicando a fórmula:
Resumindo: o aluguel médio das casas pesquisadas é R$ 335,00, sendo que o valor que mais ocorre é R$ 295,70 e o valor mediano encontrado foi R$ 315,40, ou seja, metade dos alugueis cobrados tem valor superior ao mediano e a outra metade possui valor inferior a R$ 315,40.
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
A média é uma medida que representa bem o conjunto de dados?
Consideremos os conjuntos de valores, por exemplo, de 5 provas feitas por um aluno A e um outro B:
A: 5, 5, 5, 5, 5
B: 0, 0, 5, 10, 10
Note que a média das provas de ambos alunos é a mesma, ou seja, mA = mB = 5. Porém, é nítido que os alunos não tiveram o mesmo desempenho ao longo das provas. Enquanto A se manteve constante, B foi muito mal no começo mas muito bem no final. Assim, só a média não é capaz de traduzir o conjunto de dados.
Dessa forma, com a utilização da moda e da mediana, passamos a ter uma visão melhor de como se comportam os dados em nosso conjunto (no caso que não temos acesso ao conjunto de dados brutos). Assim, vejamos uma tabela comparativa:
|
Grupo |
A |
B |
|
Média |
5 |
5 |
|
Moda |
5 |
0 e 10 |
|
Mediana |
5 |
5 |
Observando esses resultados, percebemos que o conjunto A possui uma variabilidade de notas maior que o do conjunto B, dando indícios que as notas em A foram mais homogêneas que as notas em B. Mesmo assim, para termos certeza disso, devemos calcular outras medidas estatísticas, chamadas de medidas de dispersão que estudaremos mais adiante.
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
1) Calcule a moda, a mediana e a média das seguintes séries:
i. 46, 44, 49, 45, 44, 48, 50, 42, 47
ii. 1, 1, 3, 2, 3, 5, 4, 5, 3, 3, 2, 2, 1, 1
2) Calcule a mediana e a média do conjunto de dados apresentados pela seguinte distribuição de frequências:
|
xi |
8 |
12 |
16 |
20 |
|
fi |
7 |
16 |
20 |
5 |
3) Determine a média, a moda e a mediana em cada caso:
a) Em uma casa de repouso, as pessoas internadas têm as seguintes idades:
|
idade |
Nº de pessoas |
|
67 |
3 |
|
68 |
4 |
|
71 |
3 |
|
72 |
2 |
|
73 |
4 |
|
74 |
4 |
|
75 |
5 |
|
77 |
3 |
|
78 |
2 |
|
80 |
3 |
|
84 |
4 |
|
85 |
3 |
|
total |
40 |
b) Considere a tabela, que representa a distribuição das áreas cultivadas, em hectares, de uma determinada região.
Dados: xi: área em hectares, fi: número de áreas cultivadas.
|
xi |
fi |
|
[0; 2[ |
30 |
|
[2; 4[ |
35 |
|
[4; 6[ |
60 |
|
[6; 8[ |
35 |
|
[8; 10[ |
15 |
|
[10; 12[ |
8 |
|
[12; 14[ |
2 |
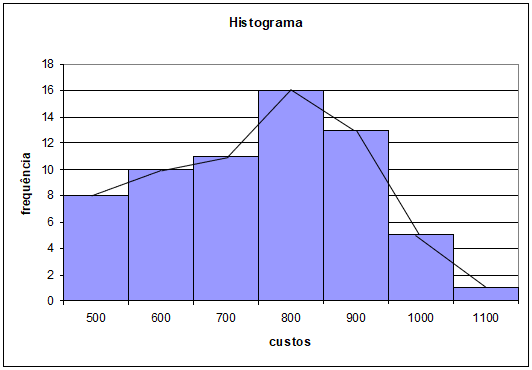
4) A tabela abaixo indica os Custos, de uma determinada empresa, com encargos salariais:
|
Custos |
fi |
|
[450; 550[ |
8 |
|
[550; 650[ |
10 |
|
[650; 750[ |
11 |
|
[750; 850[ |
16 |
|
[850; 950[ |
13 |
|
[950; 1.050[ |
5 |
|
[1.050; 1.150] |
1 |
Determine:
a) a classe modal;
b) a moda da distribuição;
c) a classe mediana;
d) a mediana da distribuição;
e) construa o histograma e o polígono de frequências da distribuição;
f) a média salarial.
5) A tabela seguinte fornece o número de erros gráficos por página de certo livro.
|
número de erros |
0 |
1 |
2 |
3 |
4 |
|
número de páginas |
84 |
25 |
8 |
2 |
1 |
Calcular:
a) o número médio de erros por página
b) o número mediano
c) qual é a moda da distribuição?
6) Numa pesquisa entre 250 famílias de certa cidade constataram-se os seguintes dados:
|
nº de filhos |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
nº de famílias |
45 |
52 |
48 |
55 |
30 |
10 |
8 |
2 |
Para a distribuição do número de filhos, calcular a média, a mediana e a moda.
7) Se os dados do problema anterior estivessem computados como segue:
|
nº de filhos |
0 |
1 |
2 |
3 |
4 |
mais do que 4 |
|
nº de famílias |
45 |
52 |
48 |
55 |
30 |
20 |
Qual das medidas (média, moda e mediana) não seria possível calcular?
8) Os dados seguintes referem-se ao tempo de vida (durabilidade) de 150 lâmpadas elétricas de certa fabricação, em centenas de horas.
|
Duração |
nº de lâmpadas |
|
0 |― 4 |
4 |
|
4 |― 8 |
12 |
|
8 |― 12 |
40 |
|
12 |― 16 |
41 |
|
16 |― 20 |
27 |
|
20 |― 24 |
13 |
|
24 |― 28 |
9 |
|
28 |― 32 |
4 |
a) Qual é a moda?
b) Calcular a vida média das lâmpadas.
c) Qual é a mediana?
9) A média dos salários dos funcionários de uma determinada empresa é 5 salários mínimos (5 SM), enquanto que a mediana é 4 SM. Sorteando-se ao acaso um dos funcionários, o que é mais provável: que ele ganhe mais ou que ele ganhe menos do que a média dos salários?
10) Uma prova foi aplicada a três classes, de 40, 48 e 46 alunos, e as médias de cada classe foram 6,0, 6,6 e 5,8, respectivamente. Qual é a média para os 134 alunos que fizeram a prova?
11) O valor com maior frequência em uma distribuição é:
a) a média b) a mediana c) a moda d) as três
12) Considere a seguinte distribuição referente a quantidade de acidentes semanais em determinado cruzamento de certa cidade:
|
nº de acidentes semanais em um cruzamento |
0 |
1 |
2 |
3 |
4 |
mais do que 4 |
|
frequência |
35 |
97 |
145 |
200 |
230 |
250 |
Qual das medidas (média, moda e mediana) não seria possível calcular?
13) Considere uma série estatística com 2351 elementos. A posição da mediana é representada pelo:
a) 1175º elemento
b) 1176º elemento
c) ponto médio entre o 1175º e o 1176º elemento
d) 1174º elemento
e) ponto médio entre o 1174º e o 1175º elemento
14) Um professor, após verificar que toda a classe obteve nota baixa, eliminou as questões que não foram respondidas pelos alunos. Com isso, as notas de todos os alunos foram aumentadas de 3 pontos. Então:
a) a média aritmética ficou alterada, assim como a mediana.
b) apenas a média aritmética ficou alterada.
c) apenas a mediana ficou alterada.
d) não houve alteração nem na média nem na mediana.
e) nada podemos afirmar sem conhecer o número total de alunos.
15) Calcule o número médio, mediano e modal de acidentes por dia em uma determinada esquina.
|
Números de acidentes por dia (xi) |
Números de dias (fi) |
|
0 |
30 |
|
1 |
5 |
|
2 |
3 |
|
3 |
1 |
|
4 |
1 |
|
Total |
40 |
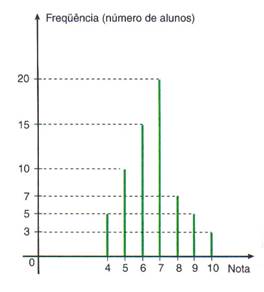
16) O gráfico a seguir mostra a distribuição de frequências das notas obtidas pelos alunos, da 2ª série do ensino médio, numa prova de Geografia. Determine:
a) a mediana dessa distribuição;
b) a moda dessa distribuição
c) a média das notas.
17) As notas de um candidato em seis provas de um concurso foram:
8,4 ; 9,1 ; 7,2 ; 6,8 ; 8,7 ; 7,2
Determine:
a) a nota média;
b) a nota mediana;
c) a nota modal.
18) Os salários-hora de cinco funcionários de uma companhia são:
R$ 75 ; R$ 90 ; R$ 83 ; R$ 142 ; R$ 88
a) qual o salário médio?
b) qual o salário mediano?
19) Considere as notas obtidas pelos alunos de uma classe em uma determinada prova:
|
Notas |
Nº de alunos |
|
2 |
1 |
|
3 |
3 |
|
4 |
6 |
|
5 |
10 |
|
6 |
13 |
|
7 |
8 |
|
8 |
5 |
|
9 |
3 |
|
10 |
1 |
Calcule:
a) a nota média;
b) a nota mediana;
c) a nota modal.
20) A partir de uma amostra de 70 pessoas obteve-se a tabela a seguir com as estaturas dos entrevistados:
|
Estaturas (cm) |
frequência |
|
150├ 158 |
5 |
|
158├ 166 |
12 |
|
166├ 174 |
18 |
|
174├ 182 |
27 |
|
182├ 190 |
8 |
Determine, para essa distribuição:
a) a média;
b) a mediana;
c) a moda.
21) Os pesos de 40 pessoas que estavam fazendo um tratamento de emagrecimento numa determinada clínica de São Paulo foram agrupados na tabela a seguir:
|
Pesos (kg) |
fi |
|
145 ├ 151 |
10 |
|
151 ├ 157 |
9 |
|
157 ├ 163 |
8 |
|
163 ├ 169 |
6 |
|
169 ├ 175 |
3 |
|
175 ├ 181 |
3 |
|
181 ├ 187 |
1 |
Determine, para essa distribuição:
a) a média;
b) a mediana;
c) a moda.
22) Considerando a distribuição abaixo, determine:
|
xi |
fi |
|
3 |
4 |
|
4 |
8 |
|
5 |
11 |
|
6 |
10 |
|
7 |
8 |
|
8 |
3 |
a) a média;
b) a mediana;
c) a moda.
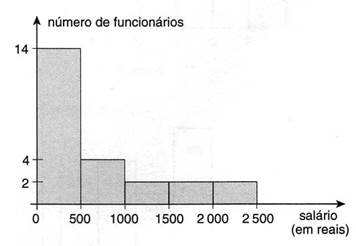
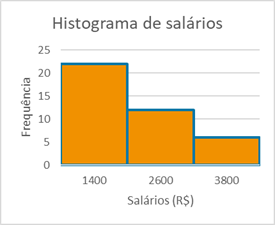
23) O histograma abaixo apresenta a distribuição de frequência das faixas salariais numa pequena empresa.
Com os dados disponíveis, calcule a média, a moda e a mediana desses salários.
24) Obtenha a mediana nos casos a seguir:
a) 12, 15, 10, 13, 11, 19
b) 7, 7, 5, 4, 3, 5, 5, 2, 3
c)
|
idade |
Frequência |
|
10 |
5 |
|
11 |
7 |
|
12 |
6 |
|
13 |
8 |
|
total |
26 |
d)
|
idade |
Frequência |
|
12 |
7 |
|
13 |
9 |
|
14 |
6 |
|
15 |
11 |
|
total |
33 |
e)
|
Salários (R$) |
Frequência |
|
500 |-- 1000 |
17 |
|
1000 |-- 1500 |
12 |
|
1500 |-- 2000 |
11 |
|
2000 |-- 2500 |
5 |
|
total |
45 |
25) Considere a tabela a seguir:
|
nº de animais domésticos em uma residência |
0 |
1 |
2 |
Mais que 3 |
|
Quantidade de residências |
66 |
94 |
31 |
191 |
Qual das medidas (média, moda e mediana) não seria possível calcular?
26) Considere uma série estatística com 4226 elementos. A mediana é representada pelo:
a) 2112º elemento
b) 2113º elemento
c) 2114º elemento
d) ponto médio entre o 2112º e o 2113º elementos
e) ponto médio entre o 2113º e o 2114º elementos
27) Em uma prova de vestibular, a banca examinadora verificou que uma questão estava mal formulada e, por isso, decidiu anular tal questão atribuindo 1 ponto a todos os candidatos. Após o acréscimo desse ponto, recalculou-se a nota média, mediana e modal obtida pelos candidatos. Pode-se dizer que:
a) Apenas a média e a moda sofreram alteração em seus valores.
b) Apenas a mediana e a moda sofreram alteração em seus valores.
c) Apenas a média e mediana sofreram alteração em seus valores.
d) A média, a moda e a mediana sofreram alteração com o acréscimo de exatamente 1 ponto.
e) A média, a moda e a mediana sofreram alteração, mas não é possível dizer em quantos pontos cada uma delas foi alterada.
28) Considere a tabela a seguir:
|
Nº de filhos |
Frequência absoluta |
|
0 |
X |
|
1 |
12 |
|
2 |
20 |
|
3 |
Y |
|
Total |
Z |
em que X < 4 e Y ≤ 5 com X,Y,Z números naturais diferentes de zero. Considere as seguintes afirmações:
I. X + Y = Z.
II. 0 < média < 3.
III. O valor modal é 20.
IV. A mediana é igual a 2.
Estão corretas as afirmações:
a) apenas II e III.
b) apenas II e IV.
c) apenas II, III e IV.
d) apenas III.
e) apenas II.
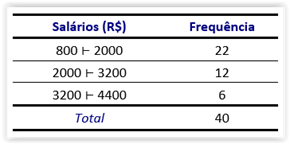
29) Foi realizada uma amostragem dentre os funcionários de uma empresa e os salários de 40 funcionários pesquisados estão classificados segundo a tabela a seguir:
Com relação à tabela:
a) Calcule o salário médio.
b) Determine o desvio padrão dos salários.
c) Determine o salário modal.
d) Construa o histograma da distribuição.
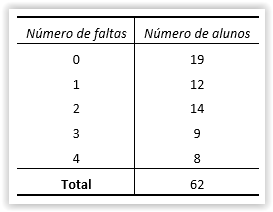
30) Em um curso semanal, há 62 alunos inscritos. No último mês, ocorreram 4 aulas. O professor contabilizou, quantas faltas tiveram os seus alunos e organizou os dados na tabela a seguir:
A tabela nos mostra que, por exemplo, 14 alunos faltaram em 2 aulas daquele mês.
a) Qual a quantidade de faltas média desses alunos?
b) Qual o valor mediano das faltas?
1) a) média=46,1 Mo = 44 Md = 46
b) média =2,6 Mo = 1 e 3 Md = 2,5
2) média =13,9 Mo = 16 Md = 16
3)a) média =75,3 Mo = 75 Md = 74,5
b) média =5,02 Mo=5 Md = 4,92
4) a) [750; 850[
b) 812,5
c) [750; 850[
d) 768,8
e)
f) 754,7
5) a) 0,425 b) 0 c) 0
6) média=2,18 Mo = 3 Md = 2
7) média não é possível calcular; Mo = 3; Md = 2.
8) a) 12,27 b) 14,53 c) 13,85
9) menos
10) 6,15
11) c
12) média e moda não conseguimos calcular; Md = 4.
13) b
14) a
15) média = 0,45 ; moda = 0; mediana = 0
16) a) 7 b) 7 c) 6,6
17) a) 7,9 b) 7,8 c) 7,2
18) a) R$ 95,6 b) R$ 88
19) a) 5,92 b) 6 c) 6
20) a) 172,4 b) 174 c) 176,6
21) a) 159,4 b) 157,8 c) 150,5
22) a) 5,4 b) 5 c) 5
23) =708,33 Mo = 291,67 Md = 428,57
24) a) 12,5
b) 5
c) 12 anos
d) 14 anos
e) R$ 1229,17
25) média, moda e mediana
26) e
27) d
28) b
29) a) R$ 2120,00
b) R$ 893,05
c) R$ 1625,00
d)
30) a) 1,60 faltas
b) 1,5 faltas
Faça o download gratuito da apostila sobre Medidas de Posição em formato PDF.
Baixe AgoraVocê também pode se interessar por:
Desvio médio, variância populacional, variância amostral, desvio padrão populacional, desvio padrão amostral e coeficiente de variação
ROL, tabelas de frequências, classes (intervalos), determinação do número de classes em uma tabela, Regra de Sturges e lista de exercícios
Espaço amostral, eventos, cálculos de probabilidades, probabilidade de um evento complementar, probabilidade da união de dois eventos