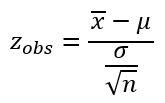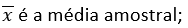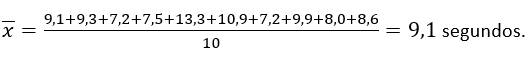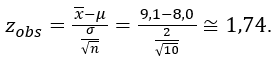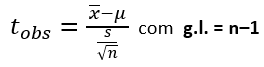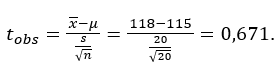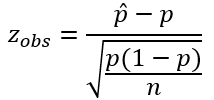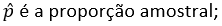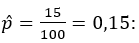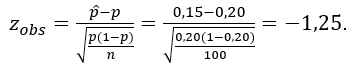Conrad Elber Pinheiro
Professor Guru
Atualizado em 30/07/2023
Ao final desta página, você pode fazer o download gratuito da apostila sobre Testes de Hipóteses em formato PDF.
Clique aqui para assistir a playlist com os conteúdos desta página no YouTube 
Neste capítulo veremos como fazer testes de hipóteses para a média populacional e para a proporção populacional quando estamos trabalhando com uma única população.
Neste capítulo veremos como fazer testes de hipóteses para a média populacional e para a proporção populacional quando estamos trabalhando com uma única população.
Quando o desvio padrão populacional σ for conhecido, a estatística do teste de hipóteses para a média é dada pela fórmula:
onde:
μ é a média populacional testada (sob H₀);
σ é o desvio padrão populacional;
n é o tamanho da amostra.
Funcionários de uma grande firma de contabilidade afirmam que a média dos salários dos contadores é menor que a de seu concorrente, que é $45000. Uma amostra aleatória de 30 contadores da firma mostrou que a média dos salários é de $43500. Sabe–se, de estudos anteriores, que o desvio padrão dos salários é $5200. Teste a afirmação dos funcionários ao nível de 5% de significância.
Resolução
Inicialmente, perceba que a frase “sabe–se, de estudos anteriores, que o desvio padrão dos salários é $5200” indica que se trata do desvio padrão populacional, ou seja, σ=5200.
O tamanho da amostra é n=30. Vamos construir nossas hipóteses nula e alternativa. Perceba que queremos testar a afirmação de que os salários dos contadores é menor que os do concorrente. Logo:
H₀: μ ≥ 45000
Hₐ: μ < 45000 (afirmação).
Vamos calcular o valor observado:
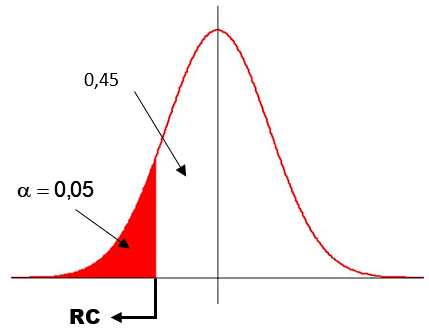
A partir da hipótese alternativa, percebemos que o nosso teste é unilateral à esquerda, ou seja, podemos construir o gráfico a seguir.
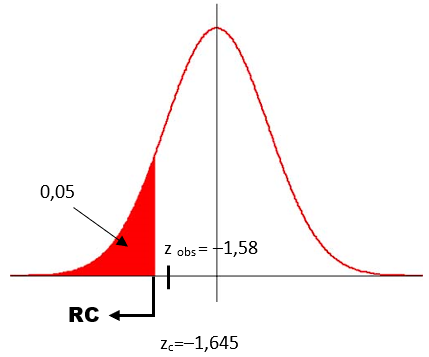
Em seguida, procuramos na tabela da Normal o valor de zc correspondente ao gráfico, ou seja, a uma probabilidade de 0,45. Concluímos que: zc=–1,645 (negativo, pois está à esquerda do zero). Marcando os valores no gráfico temos:
Clique no botão abaixo para abrir a tabela da Normal Padrão em uma nova janela.
Ver tabela da normal padrão
Note que zobs não pertence à RC. Logo, aceitamos H₀, ou seja, ao nível de significância de 5%, não há evidências de que o salário seja inferior a $45000.
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
Clique aqui para assistir a vídeo aula
Resolução do Exemplo 1
Clique aqui para fazer o download
Baixe os slides da vídeo aula gratuitamente em formato PDF.
Um pesquisador deseja estudar o efeito de certa substância no tempo de reação de seres vivos a um certo tipo de estímulo. Um experimento é desenvolvido com cobaias, que são inoculadas com a substância e submetidas a um estímulo elétrico, com seus tempos de reação (em segundos) anotados. Os seguintes valores foram obtidos: 9,1 ; 9,3 ; 7,2 ; 7,5 ; 13,3 ; 10,9 ; 7,2 ; 9,9 ; 8,0 e 8,6. Admite–se que o tempo de reação segue, em geral, o modelo Normal com média 8 segundos e desvio padrão 2 segundos. O pesquisador desconfia, entretanto, que o tempo médio sofre alteração por influência da substância. Teste essa hipótese ao nível de 6% de significância.
Resolução
Do enunciado, temos que =8s e n=10. Podemos calcular a média amostral:
Nossas hipóteses:
H₀: μ = 8
Hₐ: μ ≠ 8
Trata–se, portanto, de um teste bilateral.
Calculando o valor observado:
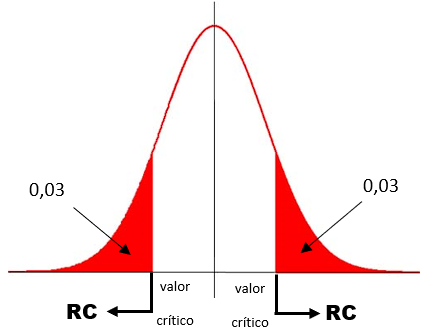
Estamos trabalhando com o seguinte gráfico:
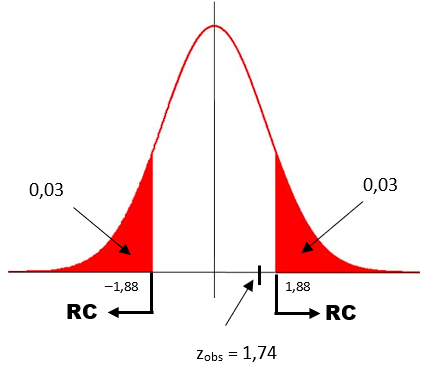
Buscando na tabela da Normal os valores críticos, temos: zc= ±1,88. Colocando esse valor no gráfico, teremos:
Como zobs não pertence à região crítica (RC), aceitamos H₀, ou seja, há evidências, ao nível de 6%, de que o tempo de reação não esteja alterado.
Na formulação das nossas hipóteses, estamos querendo verificar se a média do tempo de reação continua sendo 8 segundos. Pela nossa amostra, obtemos uma média amostral igual a 9,1 segundos, tendo evidências para se acreditar que se a média não for igual a 8, ela será maior que 8 segundos. Pensando desta forma, podemos formular o seguinte teste:
H₀: μ = 8
Hₐ: μ > 8
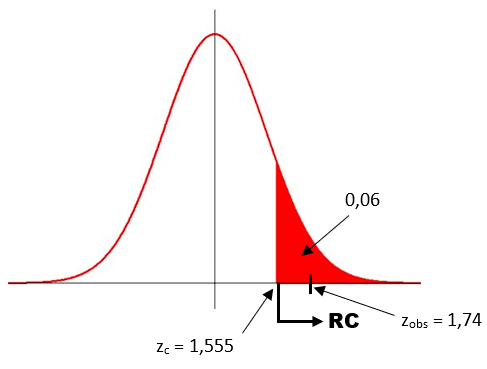
O valor zobs = 1,74 fica inalterado. Porém, o valor e a região crítica mudam:
Neste caso, vemos que o valor observado pertence à região crítica (RC), no lendo a concluir que devemos rejeitar H₀ e, portanto, aceitar Hₐ, ou seja, há evidências, ao nível de 6% de que a média seja superior a 8 segundos.
Observação: como vimos neste último exemplo, a mudança da hipótese alternativa nos levou a conclusões diferentes. Isso indica que estamos trabalhando com uma situação–limite, em que uma pequena mudança na formulação de nossas hipóteses, nos leva a uma conclusão diferente do teste. Neste caso, é aconselhável que o pesquisador faça a coleta de mais amostras (aumento do valor de n) para que esse problema seja solucionado.
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
Clique aqui para assistir a vídeo aula
Resolução do Exemplo 2
Clique aqui para fazer o download
Baixe os slides da vídeo aula gratuitamente em formato PDF.
Quando o desvio padrão populacional σ for desconhecido, optamos por trabalhar com o desvio padrão amostral s. A estatística do teste se baseará na distribuição t-Student com (n–1) graus de liberdade:
onde:
μ é a média populacional testada (sob H₀);
s é o desvio padrão populacional;
n é o tamanho da amostra.
Clique no botão abaixo para abrir a tabela da t-Student em uma nova janela.
Ver tabela da t-student
Os registros dos últimos anos de um colégio atestam para os calouros admitidos uma nota média 115 (teste vocacional). Para testar a hipótese de que a média de uma nova turma é a mesma das turmas anteriores, retirou–se uma amostra de 20 notas, obtendo–se média 118 e desvio padrão 20. Admita um nível de significância de 5% para efetuar o teste.
Resolução
Nossas hipóteses:
H₀: μ = 115
Hₐ: μ ≠ 115
Como se trata de uma amostra, vamos trabalhar com a distribuição t-Student com g.l. = n–1 = 20–1 = 19.
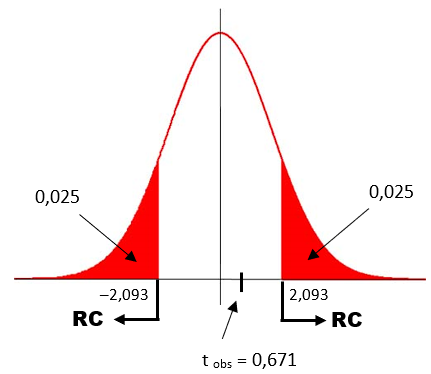
A partir da tabela da distribuição t, encontramos os valores críticos da distribuição tc = 2,093:
Como o valor observado não está na região crítica do teste, aceitamos H₀, ou seja, ao nível de 5% não há indícios de que a média tenha se alterado.
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
Clique aqui para assistir a vídeo aula
Resolução do Exemplo 3
Clique aqui para fazer o download
Baixe os slides da vídeo aula gratuitamente em formato PDF.
O teste Z para uma proporção é um teste estatístico para uma proporção populacional p. O teste Z pode ser usado quando uma distribuição binomial é dada como np ≥ 5 e nq ≥ 5. O teste estatístico é:
onde:
p é a proporção populacional;
n é o tamanho da amostra.
Um centro de pesquisas declara que menos de 20% dos usuários de Internet nos Estados Unidos tem rede sem fio em suas casas. Em uma amostra aleatória de 100 adultos, 15 deles dizem que tem rede sem fio em casa. Com um nível de 1%, há evidências suficientes para apoiar a declaração do pesquisador?
Resolução
Baseado na afirmação do pesquisador, temos as seguintes hipóteses:
H₀: p ≥ 0,20
Hₐ: p < 0,20 (afirmação)
O valor observado baseia–se na proporção amostral
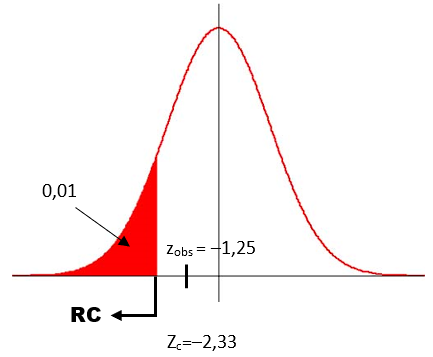
Consultado a tabela da Normal, obtemos o valor crítico do teste zc=–2,33:
Como o valor observado não pertence à região crítica do teste, aceitamos H₀, ou seja, ao nível de 1%, não há evidências de que a verdadeira proporção de usuários que possuem rede sem fio em casa seja inferior a 20%, ou ainda, podemos dizer que não podemos concordar com a afirmação do pesquisador.
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
Clique aqui para assistir a vídeo aula
Resolução do Exemplo 4
Clique aqui para fazer o download
Baixe os slides da vídeo aula gratuitamente em formato PDF.
1) Uma variável aleatória tem distribuição Normal e desvio padrão igual a 12. Estamos testando se sua média é igual ou é diferente de 20 e coletamos uma amostra de 100 valores dessa variável, obtendo uma média amostral de 17,4.
a) Formule as hipóteses.
b) Dê a conclusão do teste para os seguintes níveis de significância: 1% e 6%.
2) Um estudo foi desenvolvido para avaliar o salário de empregadas domésticas na cidade de São Paulo. Foram sorteadas e entrevistadas 200 trabalhadoras. Admita que o desvio padrão dessa variável na cidade é de 0,8 salários mínimos. Deseja-se testar se a média é igual a 3 salários mínimos ou é menor. Formule as hipóteses adequadas. Se a amostra forneceu média de 2,5 salários mínimos, qual seria a conclusão para um nível de significância de 3%?
3) A vida média de uma amostra de 100 lâmpadas de certa marca é 1615 horas. Por similaridade com outros processos de fabricação, supomos o desvio padrão igual a 120 horas. Utilizando α=5%, desejamos testar se a duração média de todas as lâmpadas dessa marca é igual ou é diferente de 1600 horas. Qual é a conclusão?
4) Deseja-se investigar se uma certa moléstia que ataca o rim altera o consumo de oxigênio desse órgão. Para indivíduos sadios, admite-se que esse consumo tem distribuição Normal com média 12 cm³/min. Os valores medidos em cinco pacientes com a moléstia foram: 14,4; 12,9; 15,0; 13,7 e 13,5. Qual seria a conclusão, ao nível de 1% de significância?
5) Uma amostra com 10 observações de uma variável aleatória Normal forneceu média de 5,5 e variância amostral 4. Deseja-se testar, ao nível de significância de 5%, se a média na população é igual ou é menor que 6. Qual é a conclusão?
6) O tempo de permanência de engenheiros recém-formados no primeiro emprego, em anos, foi estudado considerando um modelo Normal com média e variância desconhecidas. Por analogia com outras categorias profissionais, deseja-se testar se a média é 2 anos contra a alternativa de ser 3 anos. Para uma amostra de 15 engenheiros, a média obtida foi de 2,7 anos e o desvio padrão amostral 1,4 anos. Ao nível de 1%, qual a conclusão do teste?
7) Uma amostra de 25 elementos, extraída de uma população normal, resultou média 13,5 com desvio padrão de 4,4. Efetuar o teste para a hipótese: H₀: μ = 16 contra Hₐ: μ ≠ 16, ao nível de 0,05 de significância.
8) As estruturas de 20 recém-nascidos foram tomadas no Departamento de Pediatria da FMRP, cujos resultados são, em centímetros:
41 50 52 49 49 54 50 47 52 49 50 52 50 47 49 51 46 50 49 50
a) Supor inicialmente que a população das estaturas seja normal com variância de 2 cm². Testar a hipótese de que a média dessa normal é 50 cm. Admitir um risco de 5% para cometer o Erro tipo I.
b) Fazer o mesmo teste para a média, mas agora desconhecendo a variância populacional.
9) Um relatório de uma companhia afirma que 40% de toda a água obtida, através de poços artesianos no nordeste, é salobra. Há muitas controvérsias sobre essa informação, alguns dizem que a proporção é maior, outros que é menor. Para dirimir as dúvidas, 400 poços foram sorteados e observou-se, em 120 deles, água salobra. Qual seria a conclusão, ao nível de 3%?
10) Em uma cidade dos Estados Unidos, uma amostra aleatória de 85 alunos da oitava série tem nota média de 282 com desvio padrão de 35 em um teste nacional de matemática. O resultado do teste informa o administrador de uma escola estadual que a nota média do teste para os alunos da oitava série do estado é mais do que 275. Para um nível de 5%, há evidências para apoiar a afirmação do administrador?
11) Um criador tem constatado uma proporção de 10% do rebanho com verminose. O veterinário alterou a dieta dos animais e acredita que a doença diminuiu de intensidade. Um exame em 100 cabeças do rebanho, escolhidas ao acaso, indicou 8 delas com verminose. Ao nível de 8%, há indícios de que a proporção diminuiu?
12) Suponha uma amostra de tamanho 15 e um nível de confiança de 2%. Determine o valor crítico do teste de acordo com as condições:
a) em Hₐ aparece o símbolo > e é conhecido o desvio padrão amostral;
b) em Hₐ aparece o símbolo > e é conhecido o desvio padrão populacional;
c) em Hₐ aparece o símbolo < e é conhecido o desvio padrão amostral;
d) em Hₐ aparece o símbolo < e é conhecido o desvio padrão populacional;
e) em Hₐ aparece o símbolo ≠ e é conhecido o desvio padrão amostral;
f) em Hₐ aparece o símbolo ≠ e é conhecido o desvio padrão populacional.
13) As condições de mortalidade de uma região são tais que a proporção de nascidos que sobrevivem até 60 anos é de 60%. Testar essa hipótese, ao nível de 5%, se em 1000 nascimentos amostrados aleatoriamente, verificaram-se 530 sobreviventes até 60 anos.
14) Uma amostra de 500 eleitores, selecionados ao acaso, revela que 52% são favoráveis ao Partido Democrático. Poderia essa amostra ter sido retirada de uma população que tivesse 50% de eleitores democratas? Admitir α = 0,05.
15) Lança-se uma moeda 100 vezes e obtém-se 60 caras. Teste, ao nível 5%, a hipótese de que a moeda é honesta.
16) Uma pesquisa revelou que das 500 donas-de-casa consultadas, 300 preferiram o detergente X. A indústria que produz esse detergente, acredita que domina exatamente 50% do mercado. Testar a hipótese, ao nível de 4%, se a proporção de donas de casa que utiliza esse detergente é ou não é 50%.
17) A experiência tem demonstrado que 40% dos estudantes são reprovados nos exames de Estatística. Se 40 de 90 estudantes fossem reprovados, poderíamos concluir que a porcentagem de reprovação mudou? Admitir α = 5%.
Clique no botão abaixo para abrir a tabela da Normal Padrão em uma nova janela.
Ver tabela da normal padrão
Clique no botão abaixo para abrir a tabela da t-Student em uma nova janela.
Ver tabela da t-student
1) H₀: μ=20; Hₐ: μ≠20. Para 1%, aceita H₀ . Para 6%, rejeite H₀.
2) H₀: μ=3; Hₐ: μ<3. Rejeite H₀.
3) H₀: μ=1600; Hₐ: μ≠1600. Aceite H₀.
4) Média amostral: 13,9; desvio padrão amostral: s=0,8155; teste: H₀ : μ=12; Hₐ : μ ≠12. tobs = 5,18. Rejeite H₀ , ou seja, a moléstia tem influência no consumo renal médio de oxigênio ao nível de 1%.
5) H₀: μ=6; Hₐ: μ<6. tobs = –0,791 e tc=–1,833. Aceite H₀.
6) H₀: μ=2; Hₐ: μ>2. tobs = 1,936 e tc=2,624. Aceite H₀.
7) tobs = 2,84. Rejeite H₀, ou seja, com risco de 5%, a média é diferente de 16.
8) a) zobs = –2,06. Rejeite H₀, concluindo, com risco de 5%, que a média não é 50cm.
b) tobs = –1,068. Aceite H₀, ou seja, ao nível de 5% não se pode dizer que a média é diferente de 50cm.
9) zobs = –4,08. Rejeitar H₀, ou seja, o relatório da companhia não está correto.
10) H₀: μ≤275; Ha: μ>275. Rejeite H₀, ou seja, ao nível de 4%, há evidências para apoiar a afirmação do administrador de que a nota média dos alunos da oitava série é mais do que 275.
11) A incidência não diminuiu.
12) a) tc = +2,264
b) zc = +2,05
c) tc = -2,264
d) zc = -2,05
e) tc = ±2,264
f) zc = ±2,33
13) H₀: p=0,6; Hₐ: p≠0,6. zobs = –4,52. Rejeite H₀, ou seja, ao nível de 5%, a proporção de nascidos que sobrevivem até 60 anos é diferente de 60%.
14) zobs = 0,89, aceite H₀, ou seja, não há evidências, ao nível de 5%, que a proporção seja diferente de 50%.
15) zobs = 2. Rejeite H₀ (p=0,5), concluindo, ao nível de 5%, que a moeda não é honesta.
16) zobs = 4,47. Rejeite H₀, ou seja, a proporção é diferente de 50% ao nível de 5%.
17) zobs = 0,85. Aceite H₀, ou seja, não há evidências de que a porcentagem de reprovados tenha mudado.
Faça o download gratuito da apostila sobre Testes de Hipóteses em formato PDF.
Baixe Agora
Você também pode se interessar por:
Veja a relação completa de todos os conteúdos de Estatística com teoria, exemplos e exercícios.
Conceitos e propriedades da distribuição Normal, padronização, distribuição Normal Padrão, tabela da Normal Padrão, exemplos resolvidos e lista de exercícios
Intervalos de confiança para a média, proporção, variância e desvio padrão. Como usar a tabela t-Student e a tabela Qui-Quadrado.
