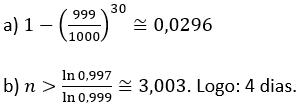Conrad Elber Pinheiro
Professor Guru
Atualizado em 28/07/2023
Para acessar a página contendo a parte teórica com exemplos resolvidos sobre Introdução à Probabilidade, clique no botão.
IR PARA TEORIA E EXEMPLOSAo final desta página, você pode fazer o download gratuito da apostila sobre Introdução à Probabilidade em formato PDF.
Clique aqui para assistir a playlist com os conteúdos desta página no YouTube
1) Lança-se um dado ao acaso. Determine a probabilidade de se obter na face superior:
a) o número 2;
b) um número maior que 4;
c) um múltiplo de 3;
d) um divisor de 20;
e) um número ímpar;
f) um número par;
g) um número primo;
h) um número maior ou igual a 6;
i) um número maior que 6.
2) Um baralho tem 52 cartas, das quais 4 são reis e 4 são valetes. Retira-se uma carta ao acaso. Determine a probabilidade de:
a) de ser retirado um rei
b) não ser retirado um valete
3) Escolhido ao acaso um elemento do conjunto dos divisores de 30, determine a probabilidade de que ele seja primo.
4) (Unesp-SP) João lança um dado sem que Antônio veja. João diz que o número mostrado pelo dado é par. A probabilidade de Antônio descobrir esse número é:
a) 1/2 b) 1/6 c) 4/6 d) 1/3 e) 3/36
5) Determine a probabilidade de se obterem os eventos a seguir, no lançamento simultâneo de 2 dados, observadas as faces voltadas para cima.
a) números iguais;
b) números diferentes;
c) números cuja soma é igual a 5;
d) números cujo produto é par;
e) números cuja soma é ímpar;
f) números cuja soma é menor que 12;
g) números cuja soma é maior que 12;
h) números primos nos 2 dados.
6) Uma urna contém 30 bolinhas numeradas de 1 a 30. Retirando-se ao acaso uma bolinha da urna, qual a probabilidade de essa bolinha ter um número múltiplo de 4 ou de 3?
7) A probabilidade de um cavalo vencer três ou menos corridas é de 58%; a probabilidade de ele vencer três ou mais corridas é de 71%. Qual é a probabilidade de o cavalo vencer exatamente três corridas?
8) Num dominó (28 peças),qual é a probabilidade de, escolhendo uma peça ao acaso, retiramos uma que tenha repetição de números (0-0, 1-1, ......, 6-6)?
9) (FGV-SP) Uma fatia de pão com manteiga pode cair no chão de duas maneiras apenas:
Uma possível distribuição de probabilidade para esses eventos é:
a) P(A) = P(B) = 3/7
b) P(A) = 0 e P(B) = 5/7
c) P(A) = –0,3 e P(B) = 1,3
d) P(A) = 0,4 e P(B) = 0,6
e) P(A) = 6/7 e P(B) = 0
10) Numa cidade com 1000 eleitores vai haver uma eleição com dois candidatos, A e B. É feita uma prévia em que os 1000 eleitores são consultados, sendo que 510 já se decidiram, definitivamente, por A. Qual é a probabilidade de que A ganhe a eleição?
11) Sabendo-se que a probabilidade de que um animal adquira certa enfermidade, no decurso de cada mês, é igual a 30%, a probabilidade de que um animal sadio venha a contrair a doença só no 3° mês é igual a:
a) 21%
b) 49%
c) 6,3%
d) 14,7%
e) 26%
12) (VUNESP) A eficácia de um teste de laboratório para checar certa doença nas pessoas que comprovadamente têm essa doença é de 90%. Esse mesmo teste, porém, produz um falso-positivo (acusa positivo em quem não tem comprovadamente a doença) da ordem de 1%. Em um grupo populacional em que a incidência dessa doença é de 0,5%, seleciona-se uma pessoa ao acaso para fazer o teste. Qual a probabilidade de que o resultado desse teste venha a ser positivo?
13) Jogando 3 dados simultaneamente, qual a probabilidade de se obter soma menor ou igual a 4 ?
14) Seja Ω = {a, b, c, d} o espaço amostral de um experimento aleatório. Consideremos a seguinte distribuição de probabilidades:
P(a) = 1/8, P(b) = 1/8, P(c) = 1/4, P(d) = x. Determine o valor de x.
15) Dos 100 alunos de uma turma, 40 gostam de Álgebra, 30 gostam de Geometria, 10 gostam de Álgebra e Geometria, e há os que não gostam de Álgebra nem de Geometria. Um aluno é escolhido ao acaso. Qual a probabilidade de ele gostar de:
a) Álgebra?
b) Geometria?
c) Álgebra e Geometria?
d) Álgebra ou Geometria?
16) Uma urna contém 3 bolas numeradas de 1 a 3 e outra urna com 5 bolas numeradas de 1 a 5. Ao retirar-se aleatoriamente uma bola de cada uma, a probabilidade de a soma dos pontos ser maior do que 4 é:
a) 3/5
b) 2/5
c) 1/2
d) 1/3
e) 2/3
17) Em uma caixa há 4 bolas verdes, 4 azuis, 4 vermelhas e 4 brancas. Se tirarmos sem reposição 4 bolas desta caixa, uma a uma, qual a probabilidade de tirarmos nesta ordem bolas nas cores verde, azul, vermelha e branca?
18) (UFSCar-SP) Uma urna tem 10 bolas idênticas, numeradas de 1 a 10. Se retirarmos uma bola da urna, determine a probabilidade de não obtermos a bola número 7.
19) (FGV-SP) Uma urna contém 50 bolinhas numeradas de 1 a 50. Sorteando-se uma bolinha, determine a probabilidade de que o número observado seja múltiplo de 8.
20) (F. Objetivo-SP) Um dado honesto tem suas faces numeradas de 1 a 6. Joga-se este dado duas vezes consecutivas. Determine a probabilidade de obter um número par no primeiro lançamento e um número maior ou igual a 5 no segundo lançamento.
21) (CESGRANRIO-RJ) Dois dados são lançados sobre uma mesa. Determine a probabilidade de ambos dados mostrarem, na face superior, números ímpares.
22) De um grupo de 200 pessoas, 160 têm fator Rh positivo, 100 têm sangue tipo O e 80 têm fator Rh positivo e sangue tipo O. Se uma dessas pessoas for selecionada ao acaso, qual a probabilidade de:
a) seu sangue ter fator Rh positivo?
b) seu sangue não ser tipo O?
c) seu sangue ter fator Rh positivo ou ser tipo O?
23) Uma moeda é viciada de tal modo que sair cara é duas vezes mais provável do que sair coroa. Calcule a probabilidade de:
a) ocorrer cara no lançamento dessa moeda;
b) ocorrer coroa no lançamento dessa moeda.
24) Os jogadores A, B, C e D disputam um torneio onde A e B têm “chances” iguais, C e D também têm “chances” iguais, mas A tem o dobro das “chances” de C. Qual a probabilidade de B vencer? Qual a probabilidade de D vencer?
25) (UFR-RJ) Os cavalos X, Y e Z disputam uma prova ao final da qual não poderá ocorrer empate. Sabe-se que a probabilidade de X vencer é igual ao dobro da probabilidade de Y vencer. Da mesma forma, a probabilidade de Y vencer é igual ao dobro da probabilidade de Z vencer. Calcule a probabilidade de:
a) X vencer;
b) Y vencer;
c) Z vencer.
26) (UF-PI) No lançamento de um dado vicioso, as faces diferentes de 5 ocorrem com probabilidade p, enquanto a face 5 ocorre com a probabilidade 3p. Assim sendo, determine o valor de p.
27) No lançamento de uma moeda defeituosa, qual a probabilidade de sair cara, sabendo-se que esta é o sêxtuplo da probabilidade de sair coroa?
28) Três carros, A, B e C, participam de uma corrida. A tem duas vezes mais probabilidades de ganhar que B e B tem três vezes mais probabilidades de ganhar que C. Determine as probabilidades de vitória de cada carro.
29) Lança-se um dado viciado, de forma que cada número par sai o triplo de vezes que cada número ímpar.
a) qual a probabilidade de ocorrer um número ímpar? E um número par?
b) Qual a probabilidade de ocorrer um número menor que 4?
c) Qual a probabilidade de que saia um número múltiplo de 2 ou 3?
30) Três corredores, A, B e C, participam de uma competição. A e B têm a mesma probabilidade de vencer e cada um tem quatro vezes mais probabilidades de vencer do que C. Calcule P(A), P(B) e P(C).
31) Uma urna I tem 3 bolas vermelhas e 4 pretas. Outra urna II tem 6 bolas vermelhas e 2 pretas. Uma urna é escolhida ao acaso e dela é escolhida uma bola também ao acaso. Qual a probabilidade de observarmos:
a) urna I e bola vermelha?
b) urna I e bola preta?
c) urna II e bola vermelha?
d) urna II e bola preta?
32) Uma urna tem 8 bolas vermelhas, 3 brancas e 4 pretas. Uma bola é escolhida ao acaso e, sem reposição desta, outra é escolhida, também ao acaso. Qual a probabilidade de:
a) a 1a bola ser vermelha e a 2a branca?
b) a 1a bola ser branca e a 2a vermelha?
c) a 1a e a 2a serem vermelhas?
d) saírem uma bola vermelha e uma bola branca?
33) A urna I tem 3 bolas vermelhas e 4 brancas, a urna II tem 2 bolas vermelhas e 6 brancas e a urna III tem 5 bolas vermelhas, 2 brancas e 3 amarelas. Uma urna é selecionada ao acaso e dela é extraída uma bola, também ao acaso. Qual a probabilidade de a bola ser:
a) vermelha?
b) branca?
c) amarela?
34) Em um lote da fábrica A existem 18 peças boas e 2 defeituosas. Em outro lote da fábrica B, existem 24 peças boas e 6 defeituosas, e em outro lote da fábrica C, existem 38 peças boas e 2 defeituosas. Um dos 3 lotes é sorteado ao acaso e dele é extraída uma peça ao acaso. Qual a probabilidade de a peça ser:
a) boa?
b) defeituosa?
35) (EU-RJ)
Protéticos e dentistas dizem que a procura por dentes postiços não aumentou. Até declinou um pouquinho. No Brasil, segundo a Associação Brasileira de Odontologia (ABO), há 1,4 milhão de pessoas sem nenhum dente na boca, e 80% delas já usam dentadura. Assunto encerrado. (Adaptado de: Veja, outubro de 1997)
Considere que a população brasileira seja de 160 milhões de habitantes. Escolhendo ao acaso um desses habitantes, a probabilidade de que ele não possua nenhum dente na boca e use dentadura, de acordo com a ABO, é de:
a) 0,28%
b) 0,56%
c) 0,70%
d) 0,80%
36) (UMC-SP) Escolhendo ao acaso uma pessoa numa certa população, a probabilidade de ela ser surda é de 0,004, a probabilidade de ela ser cega é 0,007 e a probabilidade de ela ser surda e cega é de 0,0006. A probabilidade de ela ser cega ou surda é:
a) 0,0116
b) 0,005
c) 0,011
d) 0,0104
e) 0,0011
37) A probabilidade de certo homem sobreviver mais 10 anos, a partir de certa data, é 0,4, e de que sua esposa sobreviva mais 10 anos a partir da mesma data é 0,5. Qual a probabilidade de:
a) ambos sobreviverem mais 10 anos a partir daquela data?
b) ao menos um deles sobreviver mais 10 anos a partir daquela data?
38) A probabilidade de que um aluno A resolva certo problema é P(A) = 1/2, a de que outro aluno B resolva é P(B) = 1/3 e a de que um terceiro aluno C o resolva é P(C) = 1/4. Qual a probabilidade de que:
a) os três resolvam o problema?
b) ao menos um resolva o problema?
39) Renato tem probabilidade 1/4 de convidar Alice para um passeio num domingo. A probabilidade de que César a convide é 2/5 e a de Olavo é 1/2. Admitindo que cada um deles realize o convite de modo independente, qual a probabilidade de que:
a) os três a convidem para o passeio?
b) nenhum a convide para o passeio?
c) ao menos um a convide para o passeio?
40) Em uma escola de idiomas com 2000 alunos, 500 alunos fazem o curso de inglês, 300 fazem o curso de espanhol e 200 cursam ambos os cursos.
a) Selecionando-se um estudante ao acaso, qual a probabilidade de que ele estude inglês ou espanhol?
b) Selecionando-se um estudante do curso de inglês, qual a probabilidade dele também estar cursando o curso de espanhol?
41) As probabilidades de que duas pessoas A e B resolvam um problema de modo independente uma da outra são: P(A) = 1/3 e P(B) = 3/5. Qual a probabilidade de que:
a) ambos resolvam o problema?
b) ao menos um resolva o problema?
c) nenhum resolva o problema?
d) A resolva o problema, mas B não?
e) B resolva o problema, mas A não?
42) Uma moeda não viciada é lançada 10 vezes. Qual a probabilidade de:
a) observarmos 10 caras?
b) observarmos 10 coroas?
c) observarmos 6 caras e 6 coroas?
43) Uma urna contém 20 bolas numeradas de 1 a 20. Retira-se uma bola aleatoriamente. Sejam os eventos:
A: a bola retirada possui um número múltiplo de 2;
B: a bola retirada possui um número múltiplo de 5.
Determine a probabilidade do evento A U B.
44) Uma pesquisa realizada entre 1000 consumidores, registrou que 650 deles trabalham com cartões de crédito da bandeira MasterCard, que 550 trabalham com cartões de crédito da bandeira VISA e que 200 trabalham com cartões de crédito de ambas as bandeiras. Qual a probabilidade de ao escolhermos deste grupo uma pessoa que utiliza a bandeira VISA, ser também um dos consumidores que utilizam cartões de crédito da bandeira MasterCard?
45) Uma urna contém 6 bolas pretas, 2 bolas brancas e 10 amarelas. Uma bola é escolhida ao acaso. Qual a probabilidade de:
a) a bola não ser amarela?
b) a bola ser branca ou preta?
c) a bola não ser branca, nem amarela?
46) Em um circuito elétrico, 3 componentes são ligados em série e trabalham independentemente um do outro. As probabilidades de falharem o 1º, 2º e 3º componentes valem respectivamente p1 = 0,1, p2 = 0,1 e p3 = 0,2. Qual a probabilidade de que não passe corrente pelo circuito?
47) (Vunesp-SP) Para uma partida de futebol, a probabilidade de o jogador R não ser escalado é 0,2, e a probabilidade de o jogador S ser escalado é 0,7. Sabendo que a escalação de um deles é independente da escalação do outro, determine a probabilidade de dois jogadores serem escalados.
48) (EU-RJ)
Suponha haver uma probabilidade de 20% para uma caixa de Microvlar ser falsificada. Em duas caixas, a probabilidade de pelo menos uma delas ser falsa é:
a) 4%
b) 16%
c) 20%
d) 32%
e) 36%
49) (U. F. São Carlos-SP) Gustavo e sua irmã Caroline viajaram de férias para cidades distintas. Os pais recomendam que ambos telefonem quando chegarem ao destino. A experiência em férias anteriores mostra que nem sempre Gustavo e Caroline cumprem esse desejo dos pais. A probabilidade de Gustavo telefonar é 0,6 e a probabilidade de Caroline telefonar é 0,8. A probabilidade de pelo menos um dos filhos contatar os pais é:
a) 0,20
b) 0,48
c) 0,64
d) 0,86
e) 0,92
50) (Cesgranrio-RJ) As probabilidades de três jogadores marcarem um gol cobrando um pênalti são, respectivamente, 1/2, 2,5 e 5/6. Se cada um bater um único pênalti, determine a probabilidade de todos errarem.
51) Numa bolsa temos cinco moedas de R$ 1,00 e quatro de R$ 0,50. Qual a probabilidade de, ao retirarmos duas moedas, obtermos R$ 1,50?
52) Uma urna I contém uma bola vermelha e duas brancas. A urna II contém duas bolas vermelhas e uma branca. Tiramos aleatoriamente uma bola da urna I, colocamos na urna II e misturamos. Em seguida, tiramos aleatoriamente uma bola da urna II. Qual é a probabilidade de tirarmos uma bola branca da urna II?
53) A probabilidade de um aluno X resolver este problema é 3/5 e a do aluno Y é 4/7. Qual a probabilidade de que o problema seja resolvido?
54) No lançamento de um dado, qual a probabilidade de sair o número 5 ou um número par?
55) Um número é escolhido ao acaso no conjunto {1, 2, 3, ..., 20}. Verifique se são independentes os eventos:
a) X: o número é múltiplo de 3 e Y: o número é par.
b) M: o número é primo e N: o número é ímpar.
56) (FGV) Cada dia em que uma pessoa joga numa loteria, ela tem uma probabilidade de ganhar igual a 1/1000, independentemente dos resultados anteriores.
a) Se ela jogar 30 dias, qual a probabilidade de ganhar ao menos uma vez? b) Qual o número mínimo de dias em que ela deverá jogar para que a probabilidade de que ela ganhe ao menos uma vez seja maior do que 0,3%?
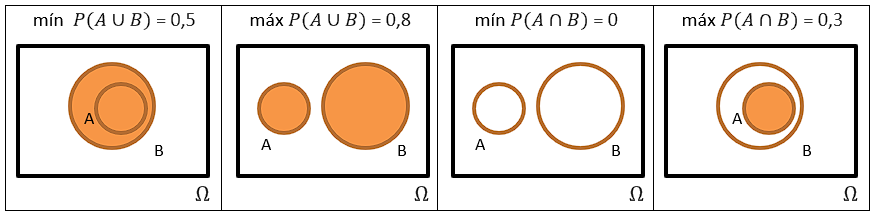
57) Sejam dois eventos quaisquer A e B contidos em um espaço amostral Ω de modo que P(A) = 0,3 e P(B) = 0,5. Determine os maiores e menores valores possíveis para P(A ∩ B) e P(A U B). Represente cada uma das quatro situações com um diagrama.
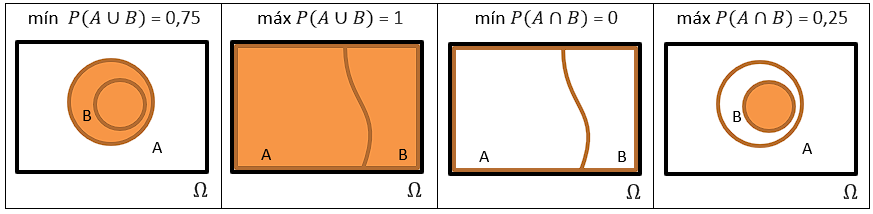
58) Sejam dois eventos quaisquer A e B contidos em um espaço amostral de modo que P(A) = 0,75 e P(B) = 0,25. Determine os maiores e menores valores possíveis para P(A ∩ B) e P(A U B). Represente cada uma das quatro situações com um diagrama.
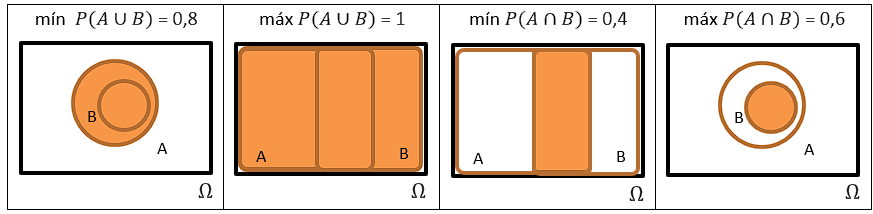
59) Sejam dois eventos quaisquer A e B contidos em um espaço amostral de modo que P(A) = 0,8 e P(B) = 0,6. Determine os maiores e menores valores possíveis para P(A ∩ B) e P(A U B). Represente cada uma das quatro situações com um diagrama.
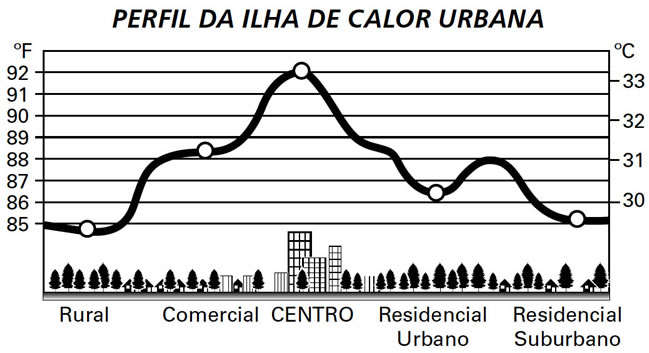
60) (ENEM) Rafael mora no Centro de uma cidade e decidiu se mudar, por recomendações médicas, para uma das regiões: Rural, Comercial, Residencial Urbano ou Residencial Suburbano. A principal recomendação médica foi com as temperaturas das “ilhas de calor” da região, que deveriam ser inferiores a 31ºC. Tais temperaturas são apresentadas no gráfico:
Escolhendo, aleatoriamente, uma das outras regiões para morar, a probabilidade de ele escolher uma região que seja adequada às recomendações médicas é
a) 1/5
b) 1/4
c) 2/5
d) 3/5
e) 3/4
61) (FUVEST) Um dado cúbico, não viciado, com faces numeradas de 1 a 6, é lançado três vezes. Em cada lançamento, anota-se o número obtido na face superior do dado, formando-se uma sequência (a, b, c). Qual é a probabilidade de que b seja sucessor de a ou que c seja sucessor de b?
a) 4/27
b) 11/54
c) 7/27
d) 10/27
e) 23/54
62) (CESGRANRIO) Joga-se N vezes um dado comum, de seis faces, não viciado, até que se obtenha 6 pela primeira vez. A probabilidade de que N seja menor do que 4 é
a) 150/216
b) 91/216
c) 75/216
d) 55/216
e) 25/216
63) (UFMG) Em uma mesa, estão espalhados 50 pares de cartas. As duas cartas de cada par são iguais e cartas de pares distintos são diferentes. Suponha que duas dessas cartas são retiradas da mesa ao acaso. Então, é CORRETO afirmar que a probabilidade de essas duas cartas serem iguais é
a) 1/100
b) 1/99
c) 1/50
d) 1/49
64) (FGV) Uma urna contém cinco bolas numeradas com 1, 2, 3, 4 e 5. Sorteando-se ao acaso, e com reposição, três bolas, os números obtidos são representados por x, y e z . A probabilidade de que xy + z seja um número par é de
a) 47/125
b) 2/5
c) 59/125
d) 64/125
e) 3/5
65) (PUCCAMP) Numa certa população são daltônicos 5% do total de homens e 0,05% do total de mulheres. Sorteando-se ao acaso um casal dessa população, a probabilidade de ambos serem daltônicos é
a) 1/1.000.
b) 1/10.000.
c) 1/20.000.
d) 1/30.000.
e) 1/40.000.
66) (MACKENZIE) Num conjunto de 8 pessoas, 5 usam óculos. Escolhidas ao acaso duas pessoas do conjunto, a probabilidade de somente uma delas usar óculos é:
a) 15/28
b) 15/56
c) 8/28
d) 5/56
e) 3/28
67) (CESGRANRIO) Em uma determinada região, constatou-se que
Seleciona-se aleatoriamente uma pessoa dessa população.A probabilidade de que seja do sexo masculino ou que não pratique exercício físico é de
a) 15%
b) 25%
c) 72,5%
d) 75%
e) 90%
68) (FMP-RS) Dois professores corrigem a prova de redação de um concurso público. O professor A corrige o dobro de provas do que o professor B. Sabe-se que 60% das provas corrigidas pelo professor A tiveram nota superior a 7, enquanto apenas 20% das provas corrigidas pelo professor B tiveram nota superior a 7. Se um candidato teve conceito não superior a 7, a probabilidade de sua prova ter sido corrigida pelo professor A é:
a) 0,85571.
b) 0,75000.
c) 0,33333.
d) 0,50000.
e) 0,25000.
1. a) 1/6 b) 1/3 c) 1/3 d) 2/3 e) 1/2 f) 1/2 g) 1/2 h) 1/6 i) 0
2. a) 1/13 b) 12/13
3. 3/8
4. D
5. a) 1/6 b) 5/6 c) 1/9 d) 3/4 e) 1/2 f) 35/36 g) 0 h) 1/4
6. 1/2
7. 29%
8. 1/4
9. D
10. 1 ou 100%
11. D
12. 1,445%
13. 1/54
14. x=1/2
15. a) 40% b) 30% c) 10% d) 60%
16. A
17. 8/1365
18. 0,9
19. 3/25
20. 1/6
21. 1/4
22. a) 4/5 b) 1/2 c) 9/10
23. a) 2/3 b) 1/3
24. B=1/3 e C=1/6
25. a) 4/7 b) 2/7 c) 1/7
26. p = 1/8
27. P(cara) = 6/7 = 0,8571
28. P(A) = 3/5 P(B) = 3/10 P(C) = 1/10
29. a) P(ímpar) = 1/4 e P(par) = 3/4 b) 5/12 c) 5/6
30. P(A) = 4/9 P(B) = 4/9 P(C) = 1/9
31. a) 3/14 b) 2/7 c) 3/8 d) 1/8
32. a) 4/35 b) 4/35 c) 4/25 d) 48/210
33. a) 11/28 b) 71/140 c) 1/10
34. a) 53/60 b) 7/60
35. C
36. D
37. a) 0,20 b) 0,70
38. a) 1/24 b) 3/4
39. a) 1/20 b) 9/40 c) 31/40
40. a) 3/10 b) 2/5
41. a) 1/5 b) 11/15 c) 4/15 d) 2/15 e) 2/5
42. a) 1/1024 b) 1/1024 c) 0
43. 3/5
44. 4/11
45. a) 4/9 b) 4/9 c) 1/3
46. 0,352
47. 0,56
48. E
49. E
50. 1/20
51. 5/9
52. 5/12
53. 29/35
54. 2/3
55. a) independentes b) dependentes
56.
57.
58.
59.
60. E
61. C
62. B
63. B
64. C
65. E
66. A
67. D
68. D
Para acessar a página contendo a parte teórica com exemplos resolvidos sobre Introdução à Probabilidade, clique no botão.
IR PARA TEORIA E EXEMPLOSFaça o download gratuito da apostila sobre Introdução à Probabilidade em formato PDF.
Baixe AgoraVocê também pode se interessar por:
Conceitos e definições de distribuições de probabilidades, valor esperado ou média de uma variável aleatória, variância e desvio padrão de uma variável aleatória, exemplos resolvidos e lista de exercícios
Ensaios de Bernoulli, conceitos de sucesso e fracasso, conceito e fórmula da distribuição Binomial, exemplos resolvidos e lista de exercícios
Conceitos e propriedades da distribuição Normal, padronização, distribuição Normal Padrão, tabela da Normal Padrão, exemplos resolvidos e lista de exercícios