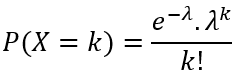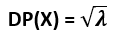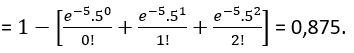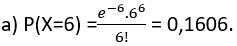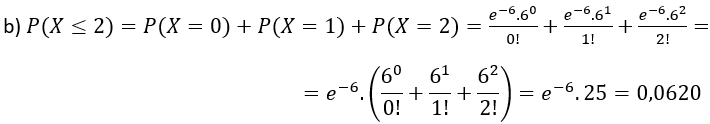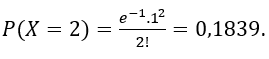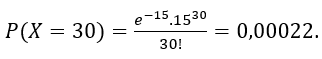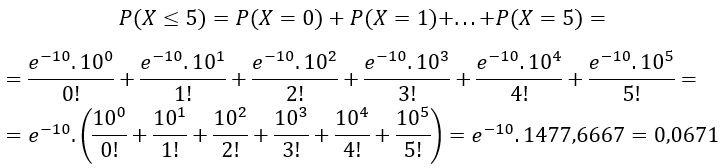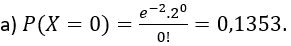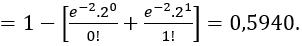Conrad Elber Pinheiro
Professor Guru
Atualizado em 29/07/2023
Ao final desta página, você pode fazer o download gratuito da apostila sobre Distribuição de Poisson em formato PDF.
Clique aqui para assistir a playlist com os conteúdos desta página no YouTube
A distribuição de Poisson (fala–se: “Poassom”) é uma distribuição de probabilidade discreta de uma variável aleatória X que satisfaz às seguintes condições:
1) O experimento consiste em calcular o número de vezes, k, que um evento ocorre em um dado intervalo. O intervalo pode ser de tempo, área, volume, etc.
2) A probabilidade de o evento acontecer é a mesma para cada intervalo.
3) O número de ocorrências em um intervalo é independente do número de ocorrências em outro intervalo.
A distribuição de Poisson possui um parâmetro λ (leia–se: “lâmbda”) que chamamos de taxa de ocorrência, que corresponde à frequência média ou esperada de ocorrências em um determinado intervalo. Além disso, sempre temos que λ>0.
A probabilidade de Poisson é calculada através da seguinte fórmula:
onde:
k=0,1,2,3,...
e é o número irracional que vale aproximadamente 2,71828;
λ é a taxa de ocorrência (que é igual à média da distribuição).
Sendo X uma variável que segue o modelo Poisson com parâmetro λ, temos que:
E(X) = λ
Var(X) = λ
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
A emissão de partículas radioativas tem sido modelada através de uma distribuição de Poisson, com o valor do parâmetro dependendo da fonte utilizada. Suponha que o número de partículas alfa, emitidas por minuto, seja uma variável aleatória seguindo o modelo Poisson com parâmetro 5, isto é, a taxa média de ocorrências é de 5 emissões a cada minuto. Calcular a probabilidade de haver mais de 2 emissões em um minuto.
Resolução
Pelo enunciado, temos que
X: número de emissões em um minuto;
λ = 5 emissões/minuto
Neste caso, queremos calcular P(X > 2), que é uma soma infinita de valores, pois podemos ter X=3,4,5,6,7,8,... Assim, devemos, obrigatoriamente, trabalhar com o complementar:
P(X > 2) = 1 – P(X ≤ 2) = 1 – [ P(X=0) + P(X=1) + P(X=2) ] =
Logo, há uma probabilidade de 87,5% de haver mais que 2 emissões ao longo de um minuto.
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
Você é o gerente de uma loja e sabe que, fora do horário de pico, entram, em média, 6 clientes a cada 10 minutos. Qual a probabilidade de entrarem:
a) 6 clientes na loja em um período qualquer de 10 minutos fora do horário de pico?
b) até 2 clientes num período de 10 minutos fora do horário de pico?
c) entrarem 3 clientes ou mais fora do horário de pico ao longo de 10 minutos?
Resolução
Inicialmente, percebemos que se trata de uma variável com distribuição de Poisson:
X: número de clientes que entram num período de 10 minutos;
λ =6 clientes a cada 10 minutos
Perceba que o cálculo ficou bastante simplificado quando colocamos o termo e⁻⁶ em evidência (fator comum).
c) Vamos utilizar o resultado do item anterior na resolução:
P(X ≥ 3) = 1 - P(X < 3) = 1 - P(X ≤ 2) = 1 - 0,0620 = 0,9380.
Note que P(X<3) = P(X=0) + P(X=1) + P(X=2) que é exatamente igual a P(X≤2).
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
No pedágio da rodovia dos Imigrantes passam, em média, 3600 carros por hora em vésperas de feriado. Qual a probabilidade de:
a) passarem dois carros em um segundo?
b) passarem 30 carros em 15 segundos?
c) passarem até 5 carros em 10 segundos?
Resolução
Pelo enunciado, temos que λ = 3600 carros/hora. Porém, se você observar as perguntas, poderá perceber que as unidades não correspondem a 1 hora. Assim, devemos recalcular o valor do nosso parâmetro a cada item, de modo a trabalharmos sempre na mesma unidade. Esse cálculo pode ser direto ou através de uma regra de três simples.
a) X: número de carros que passam no pedágio por segundo.
Nosso parâmetro será recalculado. Lembrando que 1 hora possui 3600 segundos, temos: λ = 3600/3600 = 1 carro por segundo. Agora, podemos calcular a probabilidade desejada:
b) X: número de carros que passam no pedágio a cada 15 segundos.
Vamos trabalhar, agora, com uma regra de três:
3600 carros ––––– 3600 segundos (1h)
λ –––––- 15 segundos
λ = 15 carros a cada 15 segundos. Assim:
c) X: número de carros que passam no pedágio a cada 10 segundos.
Da mesma forma que no item anterior, temos que λ = 10 carros a cada 10 segundos. Portanto:
Ou seja, há uma probabilidade de 6,71% de passarem 5 carros ou menos ao longo de 10 segundos.
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
Suponha que 360 erros de impressão estejam distribuídos aleatoriamente, segundo uma Poisson, em um livro de 180 páginas. Calcule a probabilidade de encontrar uma página com:
a) nenhum erro;
b) mais de um erro.
Resolução
Sendo X: número de erros encontrados em 1 página, devemos calcular o valor do nosso parâmetro:
λ = 360/180 = 2 erros / página.
b) P(X > 1) = 1 - P(X ≤ 1) = 1 - [P(X=0) + P(X=1)]=
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
Experiências passadas indicam que o número de ligações recebidas, no período noturno, em uma central telefônica segue uma distribuição de Poisson. As probabilidades de receber um certo número de chamadas por hora estão apresentadas na tabela a seguir:
|
N° chamadas |
Probabilidade |
|
0 |
0,0111 |
|
1 |
0,0500 |
|
2 |
0,1125 |
|
3 |
0,1687 |
|
4 |
0,1898 |
|
5 |
0,1708 |
Calcule a probabilidade de que essa central receba 3 ou mais chamadas ao longo de uma hora.
Resolução
Cuidado! Perceba que queremos calcular P(X≥3) = P(X=3) + P(X=4) + P(X=5) + ... que é uma soma infinita. Muitas vezes, essa tabela nos leva a um erro na hora do cálculo caso você não se lembre que a Poisson é válida para infinitos valores, no caso, do número de chamadas. Devemos, portanto, trabalhar com o complementar:
P(X≥3) = 1–P(X<3) = 1 – [P(X=0) + P(X=1) + P(X=2)] =
= 1 – [0,0111 + 0,0500 + 0,1125] = 0,8264 ou 82,64%.
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
1) A aplicação de fundo anticorrosivo em chapas de aço de 1 m² é feita mecanicamente e pode produzir defeitos (pequenas bolhas na pintura), de acordo com uma variável aleatória Poisson de parâmetro λ = 1 defeitos por m². Uma chapa é sorteada ao acaso para ser inspecionada. Qual a probabilidade de:
a) encontrarmos pelo menos 1 defeito?
b) no máximo 2 defeitos serem encontrados?
c) encontrar entre 2 e 4 defeitos?
d) não mais de 1 defeito ser encontrado?
2) Uma indústria de tintas recebe pedidos de seus vendedores através de fax, telefone e Internet. O número de pedidos que chegam por qualquer meio, durante o horário comercial, é uma variável aleatória discreta com distribuição Poisson com taxa de 5 pedidos por hora.
a) Calcule a probabilidade de haver mais de 2 pedidos por hora.
b) Em um dia de trabalho (8 horas), qual seria a probabilidade de haver 50 pedidos?
c) Qual a probabilidade de não haver nenhum pedido em um dia de trabalho? Você diria que isso é um evento raro?
3) O pessoal de inspeção de qualidade afirma que os rolos de fita isolante apresentam, em média, uma emenda a cada 50 metros. Admitindo que a distribuição do número de emendas é dada pela Poisson, calcule a probabilidade de encontrar:
a) nenhuma emenda em um rolo de 125 metros;
b) no máximo duas emendas em um rolo de 125 metros.
c) pelo menos uma emenda num rolo de 100 metros.
4) Certo posto de bombeiros recebe em média 3 chamadas por dia. Calcule a probabilidade de receber, em um dia:
a) 4 chamadas;
b) 3 ou mais chamadas.
5) A média de chamadas telefônicas numa hora é igual a 3. Qual a probabilidade de:
a) receber exatamente 3 chamadas em uma hora?
b) receber 4 ou mais chamadas em 90 minutos?
6) Na pintura de paredes, aparecem defeitos em média na proporção de um defeito por metro quadrado. Qual a probabilidade de aparecerem 3 defeitos numa parede de 2 x 2m?
7) Suponha que haja em média dois suicídios por ano numa população de 50000 habitantes distribuídos segundo uma Poisson. Em certa cidade com 100 000 habitantes, qual a probabilidade de que o número de suicídios em determinado ano seja:
a) igual a 0?
b) igual a 1?
c) igual a 2?
d) igual a 2 ou mais?
8) Suponha que ocorram 400 erros de impressão distribuídos aleatoriamente em um livro de 500 páginas. Encontre a probabilidade de que uma dada página contenha:
a) nenhum erro;
b) exatamente dois erros.
9) Certa loja recebe, em média, 5 clientes por hora, segundo o modelo Poisson. Qual a probabilidade de:
a) receber dois clientes em 24 minutos?
b) receber pelo menos três clientes em 18 minutos?
10) A média de chamadas telefônicas em uma hora é três, segundo o modelo Poisson. Qual a probabilidade de receber:
a) três chamadas em 20 minutos?
b) no máximo duas chamadas em meia hora?
11) Em uma estrada passam, em média, 1,7 carros por minuto. Qual a probabilidade de passarem exatamente dois carros em dois minutos? Admita válido o modelo Poisson.
12) Uma fábrica produz tecidos com 2,2 defeitos, em média, por peça, segundo o modelo Poisson. Determine a probabilidade de haver ao menos dois defeitos em duas peças.
1) a) 0,632 b) 0,920 c) 0,261 d) 0,736
2) a) 0,875 b) 0,018 c) Sim, pois a probabilidade é de e⁻⁴⁰.
3) a) 0,0821 b) 0,5440 c) 0,8647
4) a) 0,1680 b) 0,5767
5) a) 0,2241 b) 0,6580
6) 0,1954
7) a) 0,0183 b) 0,0732 c) 0,1464 d) 0,9085
8) a) 0,449 b) 0,1438
9) a) 0,2707 b) 0,1912
10) a) 0,0613 b) 0,8088
11) 0,1929
12) 0,9337
Faça o download gratuito da apostila sobre Distribuição de Poisson em formato PDF.
Baixe AgoraVocê também pode se interessar por:
Conceitos e fórmula da Distribuição Geométrica, esperança, variância e lista de exercícios
Conceitos e propriedades da distribuição Normal, padronização, distribuição Normal Padrão, tabela da Normal Padrão, exemplos resolvidos e lista de exercícios
Conceitos e definições de distribuições de probabilidades, valor esperado ou média de uma variável aleatória, variância e desvio padrão de uma variável aleatória, exemplos resolvidos e lista de exercícios