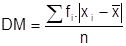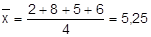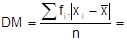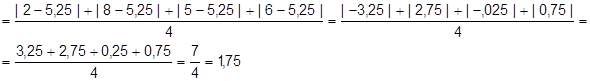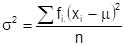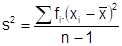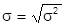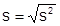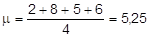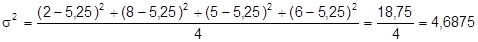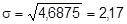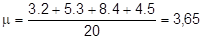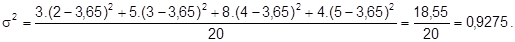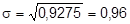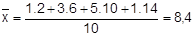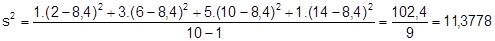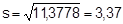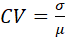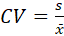Conrad Elber Pinheiro
Professor Guru
Atualizado em 23/07/2023
Ao final desta página, você pode fazer o download gratuito da apostila sobre Medidas de Dispersão em formato PDF.
Clique aqui para assistir a playlist com os conteúdos desta página no YouTube
Conforme dissemos anteriormente, as medidas de tendência central não são suficientes para caracterizar totalmente uma sequência numérica. Se observarmos as sequências:
X: 10, 1, 18, 20, 35, 3, 7, 15, 11, 10.
Y: 12, 13, 13, 14, 12, 14, 12, 14, 13, 13.
Z: 13, 13, 13, 13, 13, 13, 13, 13, 13, 13.
concluiremos que todas possuem a mesma média 13. No entanto, são sequências completamente distintas do ponto de vista da variabilidade de dados.
Na sequência Z não há variabilidade de dados, visto que todos os valores coincidem com a média. Na sequência Y, a média 13 representa bem a série, mas existem elementos da série levemente diferenciados da média 13, ou seja, há baixa variabilidade. Na sequência X existem muitos elementos bastante diferenciados da média 13, indicando uma alta variabilidade ao redor da média.
Para avaliar o grau de variabilidade dos dados em torno da média, usaremos as medidas de dispersão: desvio médio, variância e desvio padrão.
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
O conceito estatístico de desvio corresponde ao conceito matemático de distância. A dispersão dos dados em relação à média de uma sequência pode ser avaliada através dos desvios de cada elemento da sequência em relação à média da sequência. O desvio médio é definido como sendo uma média aritmética dos desvios de cada elemento da série para a média da série, ou seja,
Considere as notas 2, 8, 5, 6 obtidas por 4 alunos, numa avaliação de Biologia. Determine o desvio médio.
Inicialmente, calcularemos a média:
Agora, calculamos o desvio médio, lembrando que fi = 1, visto que cada um dos quatro valores apareceu uma única vez.
Interpretação: Em média, cada elemento da sequência está afastado do valor 5,25 por 1,75 unidades.
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
Pelo exemplo anterior, observamos que a dificuldade em se operar o DM se deve à presença do módulo, para que as diferenças x i – média possam ser interpretadas como distâncias. Outra forma de se conseguir que as diferenças xi – se tornem sempre positivas ou nulas é considerar o quadrado destas diferenças, isto é, (xi – média)² . Se substituirmos, na fórmula do DM a expressão por (xi – média)² , obteremos nova medida de dispersão chamada variância.
A variância populacional é representada por σ² (sigma ao quadrado), enquanto que a variância amostral é representada por s². O símbolo σ é a letra grega minúscula sigma.
A fórmula da variância populacional é:
A fórmula da variância amostral é:
O desvio padrão é definido como sendo a raiz quadrada da variância.
Dessa forma, a fórmula do desvio padrão populacional é:
E a fórmula do desvio padrão amostral é:
Quando estamos trabalhando com uma amostra, sem conhecermos o verdadeiro valor da média ou do desvio padrão, admitimos que a média da amostra esteja próxima do valor da média populacional, e que a variância da amostra (variância amostral) esteja próxima da variância populacional. A raiz quadrada da variância amostral é chamada desvio padrão amostral.
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
É natural a pergunta: qual das duas medidas é melhor? Na verdade, não há uma melhor que a outra, visto que são idênticas (basta extrair a raiz de uma ou elevar a outra ao quadrado). Porém, o desvio-padrão é muito melhor no sentido de facilitar a interpretação. Por exemplo, se calcularmos a variância de uma variável X que representa a idade em um conjunto de dados obtendo Var(X) = 25 anos^2, teríamos dificuldades de interpretar o resultado. Afinal, qual o significado de anos ao quadrado? Porém, o desvio-padrão nos daria DP(X) = 5 anos, que possui uma interpretação concreta.
Isso ocorre porque no cálculo da variância, quando elevamos ao quadrado a diferença (xi–média), a unidade de medida da série fica também elevada ao quadrado. Portanto, a variância é dada sempre no quadrado da unidade de medida da série. Se os dados são expressos em metros, a variância é expressa em metros quadrados. Em algumas situações, a unidade de medida da variância nem faz sentido. É o caso, por exemplo, em que os dados são expressos em litros. A variância será expressa em litros quadrados.
Portanto, o valor da variância não pode ser comparado diretamente com os dados da série, ou seja: variância não tem interpretação.
Exatamente para suprir esta deficiência da variância é que se utiliza o desvio padrão. Como o desvio padrão é a raiz quadrada da variância, o desvio padrão terá sempre a mesma unidade de medida da série e, portanto admite interpretação.
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
Vejamos alguns exemplos de como calcular a variância e o desvio padrão em um conjunto de dados.
Considere as notas 2 – 8 – 5 – 6 obtidas por 4 alunos, numa avaliação de Biologia, distribuídas na tabela abaixo. Calcule o desvio padrão considerando-se uma população.
Cálculo da média:
Cálculo da variância populacional:
O desvio padrão corresponde à raiz quadrada da variância:
Assim, os dados estão, em média, afastados de 5,25 por 2,17 unidades.
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
Calcule o desvio padrão da série abaixo, considerando-se uma população.
|
xi |
fi |
|
2 |
3 |
|
3 |
5 |
|
4 |
8 |
|
5 |
4 |
|
Total |
20 |
Cálculo da média:
Cálculo da variância populacional:
O desvio padrão corresponde à raiz quadrada da variância:
Assim, os dados variam, em média, 0,96 unidades ao redor da média 3,65.
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
Calcule o desvio padrão da série abaixo, representativa de uma amostra.
|
Classe |
Int. classe |
fi |
xi |
|
1 |
0 |― 4 |
1 |
2 |
|
2 |
4 |― 8 |
3 |
6 |
|
3 |
8 |― 12 |
5 |
10 |
|
4 |
12 |― 16 |
1 |
14 |
|
|
Total |
10 |
-- |
Cálculo da média:
Cálculo da variância amostral:
O desvio padrão amostral corresponde à raiz quadrada da variância amostral:
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
Vamos imaginar duas pessoas A e B. O indivíduo A possui R$ 10 na sua carteira e, desse valor, ele perde R$ 2. O indivíduo B possui R$ 100 e perde R$ 5. Podemos fazer duas perguntas:
Qual das pessoas perdeu mais dinheiro?
Qual das pessoas perdeu, proporcionalmente, mais dinheiro?
Para a primeira questão, fica evidente que foi o indivíduo B, visto que R$ 5 é maior que R$ 2. Porém, quando analisamos relativamente, a resposta da questão 2 passa a ser o indivíduo A, pois, percentualmente, A perdeu 2/10 = 0,2 ou 20% do que possuía na carteira enquanto que B perdeu 5/100 = 0,05 ou 5% do que possuía. Esse conceito de relatividade é exatamente o que propõe o coeficiente de variação.
Transformando o problema anterior em termos estatísticos, se uma série X apresenta média igual a 10 e desvio padrão igual a 2 e uma série Y apresenta média igual a 100 e desvio padrão igual a 5, do ponto de vista da dispersão absoluta, a série Y apresenta maior dispersão que a série X. No entanto, se levarmos em consideração as médias das séries, o desvio padrão de Y que é 5 em relação a 100 é um valor menos significativo que o desvio padrão de X que é 2 em relação a 10.
O coeficiente de variação é indicado por
ou
Calculando, então, o coeficiente de variação das séries citadas tem:
CV(X) = 2 / 10 = 0,2 ou 20%
CV(Y) = 5 / 100 = 0,05 ou 5%
Comparando os valores destes dois coeficientes concluímos que a série X admite maior dispersão relativa. Como a medida de dispersão relativa leva em consideração a medida de dispersão absoluta e a média da série, é uma medida mais completa que a medida de dispersão absoluta.
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
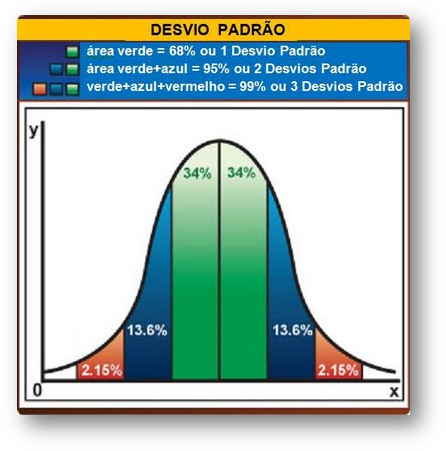
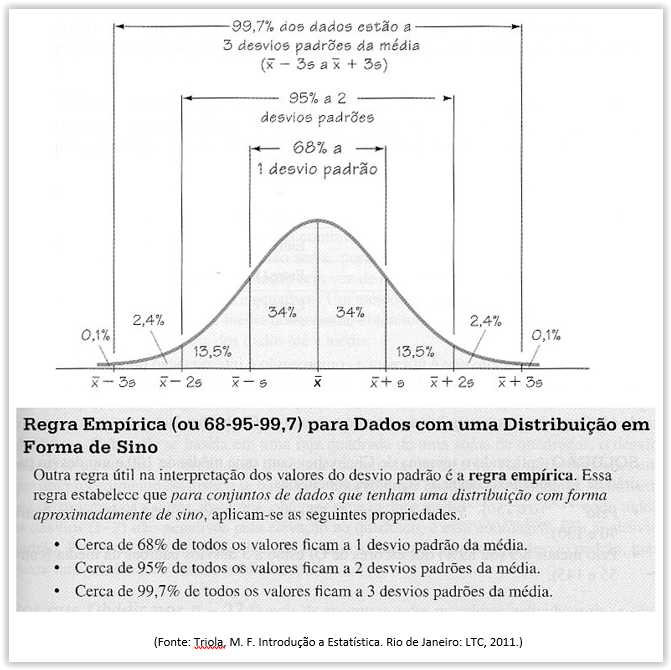
Quando temos um conjunto de dados cuja distribuição é Normal, o formato de seu histograma se assemelha a de um sino, é uma curva simétrica e, ainda, a média a moda e a mediana possuem exatamente o mesmo valor (ou são, no caso de uma amostra, muito próximos), conforme vemos na figura a seguir.
Esses percentuais 68%, 95% e 99% citados na interpretação serão comprovadas, com maior precisão, no estudo da distribuição normal de probabilidades. Quando a distribuição não é perfeitamente simétrica estes percentuais apresentam pequenas variações para mais ou para menos, dependendo do caso.
Se um conjunto tiver média µ = 100 e desvio padrão σ = 5, podemos interpretar estes valores da seguinte forma:
a) Os valores da série estão concentrados em torno de 100.
b) O intervalo [95, 105] contém aproximadamente, 68% dos valores da série.
c) O intervalo [90, 110] contém aproximadamente, 95% dos valores da série.
d) O intervalo [85, 115] contém aproximadamente, 99% dos valores da série.
É importante perceber que, ao aumentar o tamanho do intervalo, aumenta-se o percentual de elementos contido no intervalo.
Foi observado que as contas de luz para uma área municipal, no mês de junho, são normalmente distribuídas. Se a média das contas for $ 42,00 e o desvio padrão populacional foi $ 12,00, entre que intervalo de valores estão 68% das contas? E 95% das contas?
µ – σ = 42,00 – 12,00 = 30,00
µ + σ = 42,00 + 12,00 = 54,00
Logo, 68% das contas estão entre os valores de $ 30,00 e $ 54,00.
µ – 2 σ = 42,00 – 2 . 12,00 = 42,00 – 24,00 = 18,00
µ + 2 σ = 42,00 + 2 . 12,00 = 42,00 + 24,00 = 66,00
Portanto, 95% das contas estão entre os valores de $ 18,00 e $ 66,00.
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
1) Calcule o desvio padrão da distribuição populacional:
|
Classes |
fi |
|
2 |― 6 |
5 |
|
6 |― 10 |
12 |
|
10 |― 14 |
21 |
|
14 |― 18 |
15 |
|
18 |― 22 |
7 |
2) Em um exame final de Matemática, o grau médio de um grupo de 150 alunos foi 7,8 e o desvio padrão, 0,80. Em Estatística, entretanto, o grau médio final foi 7,3 e o desvio padrão, 0,76. Em que disciplina foi maior a dispersão?
3) Medidas as estaturas de 1017 indivíduos, obtivemos média igual a 162,2 cm e s = 8,01 cm. O peso médio desses mesmos indivíduos é 52 kg, com um desvio padrão de 2,3 kg. Esses indivíduos apresentam maior variabilidade em estatura ou em peso?
4) Um grupo de 85 moças tem estatura média de 160,6 cm, com um desvio padrão igual a 5,97 cm. Outro grupo de 125 moças tem uma estatura média de 161,9 cm, sendo o desvio padrão igual a 6,01 cm. Qual é o coeficiente de variação de cada um dos grupos? Qual o grupo mais homogêneo?
5) Um grupo de cem estudantes tem uma estatura média de 163,8 cm, com um coeficiente de variação de 3,3%. Qual o desvio padrão desse grupo?
6) Uma distribuição apresenta as seguintes estatísticas: σ = 1,5 e CV = 2,9%. Determine a média da distribuição.
7) Numa fábrica de rolamentos, retirou-se da produção de um determinado dia uma amostra de 10 rolamentos, dos quais se mediu o diâmetro externo, em mm, obtendo-se:
|
20,2 |
21,4 |
20,8 |
19,6 |
22,1 |
|
21,7 |
20,4 |
22,0 |
20,5 |
19,3 |
Calcular a média e o desvio padrão desta amostra.
8) Calcular a média e o desvio padrão da seguinte distribuição amostral de uma variável X.
|
faixas de observações |
frequência |
|
0 |― 10 |
25 |
|
10 |― 20 |
48 |
|
20 |― 30 |
66 |
|
30 |― 40 |
44 |
|
40 |― 50 |
17 |
|
Total |
200 |
9) Em 120 experimentos, onde cada um consiste em lançar 3 moedas e contar o número de caras, obtivemos os seguintes resultados:
|
Nº de caras |
0 |
1 |
2 |
3 |
|
Nº de experimentos |
18 |
40 |
49 |
13 |
Calcular a média, a variância e o desvio padrão do número de caras observado nos experimentos.
10) Uma amostra de 900 lâmpadas foi testada para se determinar a durabilidade. Os dados foram:
|
Durabilidade em horas |
frequência |
|
1000 |― 1400 |
150 |
|
1400 |― 1800 |
300 |
|
1800 |― 2200 |
450 |
|
Total |
900 |
Na amostra testada
a) qual é a porcentagem de lâmpadas que duraram menos de 1800 horas?
b) qual é a durabilidade média?
c) qual é o desvio padrão?
11) A tabela representa as estaturas de 35 crianças nascidas numa mesma maternidade numa certa semana.
|
estatura (cm) |
no de crianças |
|
45 ├── 46 |
1 |
|
46 ├── 47 |
4 |
|
47 ├── 48 |
6 |
|
48 ├── 49 |
12 |
|
49 ├── 50 |
8 |
|
50 ├── 51 |
3 |
|
51 ├── 52 |
0 |
|
52 ├── 53 |
1 |
Determinar a média e o desvio-padrão das estaturas destas crianças ao nascerem.
12) Um restaurante cobra o almoço de cada cliente através do peso (por quilo) da quantidade de alimento consumida. Foi observado, durante um mês, que as quantidades de alimento consumidas são normalmente distribuídas. Se a média consumida for 550 g e o desvio padrão 200 g, calcular:
a) a amplitude dos 95% centrais.
b) a amplitude dos 99% centrais.
13) Os pratos produzidos por uma indústria têm diâmetro médio de 19 cm e desvio padrão de 0,2 cm. Dois pratos A e B cujos diâmetros medem respectivamente 19,8 cm e 18,3cm serão testados pelo Controle Estatístico de Qualidade, que admite uma tolerância de três desvios acima e três abaixo da média. Assinale a alternativa correta:
a) O prato A será aprovado
b) Ambos os pratos serão reprovados
c) o prato A será reprovado e o prato B aprovado
d) o prato B será reprovado.
14) O desvio padrão de um conjunto de dados é 16. A variância será:
a)16
b) 64
c) 256
d) 4
15) A variância de um conjunto de dados é 16. O desvio padrão será:
a) 4
b) 256
c) 36
d) 2
16) Calcule o desvio padrão das seguintes populações:
a) X: 2, 3, 7, 9, 11, 13.
b) Y: 5, 12, 4, 20, 13, 17.
17) Calcule o desvio padrão das seguintes amostras:
a) Z: 15, 16, 17, 20, 21.
b) T: 6, 5, 10, 12, 19.
18) Uma fábrica corta bambus para a confecção de cercas. Cada corte deve ter um comprimento médio de 180cm e apresenta um desvio-padrão de 1,5cm. Após cortados, os bambus passam por um controle de qualidade que rejeita cortes que estejam com 2 desvios-padrão acima ou abaixo da média especificada. Seis bambus, A, B, C D, E e F foram medidos pelo controle de qualidade e os valores obtidos são apresentados na tabela a seguir. Quais deles o controle deve aprovar e quais deve rejeitar?
|
bambu |
comprimento |
|
A |
178,5cm |
|
B |
183,4cm |
|
C |
176,2cm |
|
D |
175,8cm |
|
E |
182,7cm |
|
F |
180,0 cm |
19) Considere a tabela seguinte que mostra o número de unidades vendidas por dia de certo produto numa loja:
|
Nº de unid. vendidas por dia |
Nº de dias |
|
0 |
15 |
|
1 |
13 |
|
2 |
11 |
|
3 |
8 |
|
4 |
3 |
|
Total |
|
Determine:
a) o desvio padrão amostral;
b) o coeficiente de variação;
c) o desvio médio.
20) Seja a amostra:
|
idade |
Frequência absoluta |
|
10 ├ 20 |
10 |
|
20 ├ 30 |
7 |
|
30 ├ 40 |
3 |
|
Total |
20 |
Determine:
a) a média;
b) a variância;
c) o desvio-padrão;
d) o coeficiente de variação;
e) o desvio médio.
21) Dados: CV=7,3% e média amostral =25, calcule o desvio padrão amostral.
22) Dados CV=12% e s=36, calcule a média amostral.
23) Uma máquina empacota café com média 500g e desvio padrão 12g. O controle de qualidade da empresa rejeita pacotes cujo peso ultrapasse 2 desvios padrão da média. Qual dos pacotes a seguir serão rejeitados pelo controle de qualidade?
A = 515 g
B = 490 g
C = 470 g
D = 525 g
E = 477 g
F = 500 g
G = 532 g
24) Os tempos despendidos por 12 alunos, elementos de uma população, em segundos para percorrer certo trajeto foram
16, 17, 16, 20, 18, 16, 17, 19, 21, 22, 16, 23.
Sem agrupar os dados, calcule:
a) a moda;
b) a mediana;
c) a média;
d) a variância;
e) o desvio padrão;
f) o coeficiente de variação.
25) Realizou-se medições das áreas, em metros quadrados, de 50 terrenos. De posse desses dados, calculou-se a área média, o desvio padrão e a variância das medidas. Os valores obtidos estão representados, respectivamente, nas unidades:
a) m², m², m²
b) m², m², m⁴
c) m², m⁴, m²
d) m, m, m²
e) m, m², m
26) Veja o trecho a seguir extraído de um livro de Estatística:
A distribuição em forma de sino mencionada pelo autor é, na verdade, a Distribuição Normal de Probabilidades. Com base nessas informações, resolva o problema a seguir, proposto pelo mesmo autor.
Os escores de QI têm uma distribuição em forma de sino, com média de 110 e desvio padrão de 15. Qual a porcentagem de escores de QI entre 80 e 140? Justifique.
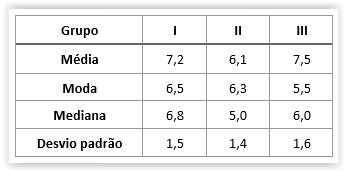
27) Três grupos distintos de estudantes (identificados por I, II e III) realizaram uma mesma prova da disciplina Probabilidade Avançada. As provas foram corrigidas seguindo um mesmo critério e as notas poderiam variar de 0 a 10. As principais estatísticas obtidas para as provas desses três grupos estão apresentadas na tabela a seguir:
Qual dos três grupos apresentou desempenho mais homogêneo nessa prova? Justifique a sua resposta com cálculos e/ou com palavras.
1) σ=4,45
2) CV(Mat)=0,103 ; CV (Estat)=0,104. Logo a maior dispersão foi na Estatística.
3) CV (altura)=0,0493 ; CV(peso)=0,0442. Maior variabilidade na altura.
4) CV(85) = 0,03717 CV(125) = 0,03712 grupo de 125 pessoas é mais homogêneo. Porém, como a diferença nos coeficientes de variação ocorre apenas na quinta casa decimal, dizemos, na prática, que os dois grupos possuem mesma homogeneidade.
5) 5,4054
6) 51,72
7) média=20,8 ; variância=0,9556 ; s=0,9775
8) média =24 ; variância =129,6482 ; s=11,39
9) média =1,475 ; variância =0,7725 ; s=0,88
10) a) 50% b) 1733,3 h c) 298,3 h
11) média =48,5 ; s=1,40
12) a) [150 ; 950] b) [0 ; 1150]
13) B
14) C
15) A
16) a) σ=3,99 b) σ=5,81
17) a) s=2,59 b) s=5,59
18) Aprovados: A, E, F ; Reprovados: B, C, D
19) a) s=1,25 b) 0,88 ou 88% c) 1,0704
20) a) 21,5 b) 55,5263 c) 7,45 d) 34,7% e) 6,5
21) 1,825
22) 300
23) Rejeitados: C, D, G.
24) a) 16 s
b) 17,5 s
c) 18,42 s
d) 5,9097 s²
e) 2,43 s
f) 0,138 ou 13,8%
25) B
26) 95%
27) Grupo I, pois tem o menor coeficiente de variação.
Faça o download gratuito da apostila sobre Medidas de Dispersão em formato PDF.
Baixe AgoraVocê também pode se interessar por:
ROL, tabelas de frequências, classes (intervalos), determinação do número de classes em uma tabela, Regra de Sturges e lista de exercícios
Fórmulas e cálculos da média, moda e mediana e lista de exercícios
Intervalos de confiança para a média, proporção, variância e desvio padrão. Como usar a tabela t-Student e a tabela Qui-Quadrado.