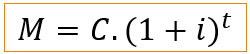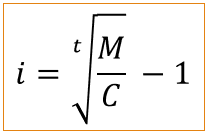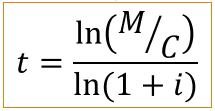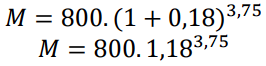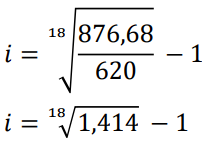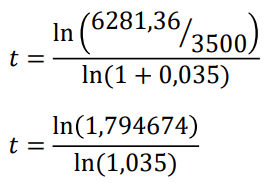Conrad Elber Pinheiro
Professor Guru
Atualizado em 03/08/2023
Clique aqui para assistir a playlist com os conteúdos desta página no YouTube
Ao trabalhar com juros simples e juros compostos, existem alguns conceitos fundamentais que devemos conhecer. Veja a lista de definições e nomenclaturas que serão utilizadas neste capítulo.
Capital (C) – é o valor inicial da rentabilidade (muitas vezes chamado de capital investido).
Juros (J) – é o valor da rentabilidade que pode ocorrer de forma diária, mensal, anual, trimestral, semestral, etc.
Montante (M) – é o valor final composto pelo capital somado aos juros.
Tempo (t) – é a duração do investimento. O tempo deve ter a mesma unidade que a taxa.
Taxa (i) – é o valor, na forma de porcentagem, da rentabilidade que poderá ser diária, mensal, anual, etc. Nos cálculos, a porcentagem deverá ser convertida para um número decimal, bastando dividir a porcentagem por 100.
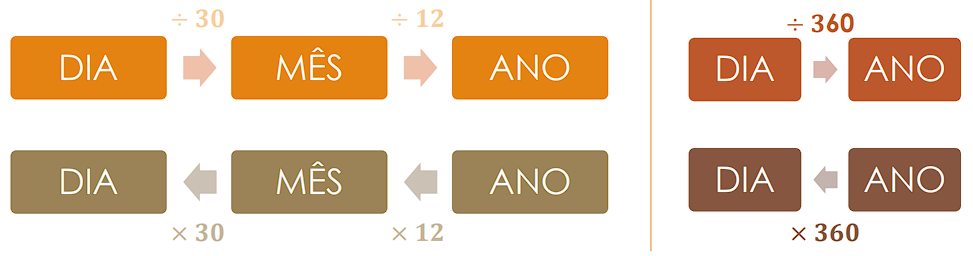
Sempre que a unidade do tempo (t) for diferente da unidade da taxa (i), devemos converter o tempo. O esquema a seguir ilustra as operações que devemos fazer para as conversões de tempo. Por exemplo: para transformar um número em anos para meses, devemos multiplicar por 12. Já para transformar o número de meses em anos, dividimos por 12.
A figura a seguir ilustra um diagrama com dois exemplos de conversões de tempo entre dias, meses e anos:
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
É um sistema de capitalização em que os juros são sempre os mesmos para todos os meses (no caso de se trabalhar com uma capitalização mensal). Ou seja, o valor dos juros é calculado uma única vez sobre o capital inicial e é aplicado em todos os meses considerados na capitalização. Existem casos em que cálculos judiciais utilizam os juros simples.
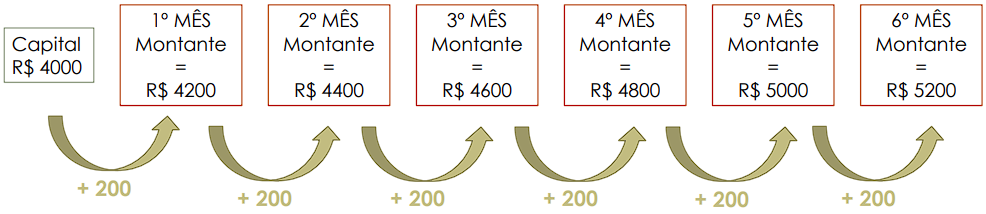
Para compreender melhor a lógica, os cálculos e as fórmulas de juros simples, vamos analisar um exemplo que ilustra o fluxo de juros.
Suponhamos os seguintes dados:
Capital: C = R$ 4000
Taxa mensal: i = 5% = 0,05
Tempo: 6 meses
Logo, os juros aplicados mensalmente serão:
5% de 4000
0,05 . 4000 = R$ 200
A figura a seguir ilustra como serão calculados os juros e o montante a cada mês:
Portanto, após 6 meses, teremos:
Juros totais: 6 meses . R$ 200 = R$ 1200
Montante: Capital + Juros = 4000 + 1200 = R$ 5200
Em juros simples, trabalhamos basicamente com duas fórmulas:
J = C . i . t
M = C + J
Em que:
J = juros
C = capital
i = taxa
t = tempo
M= montante
Observação: o tempo (t) deve estar na mesma unidade da taxa (i).
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
Um capital de R$ 2500,00 foi aplicado, a juros simples, a uma taxa de 2,5% a.m. por um período de 12 meses.
a) Qual o valor total dos juros?
b) Qual o valor total disponível nessa aplicação no final do período?
Resolução
a) Do enunciado, temos:
C = 2500
i = 2,5% = 0,025
t = 12
J = C . i . t
J = 2500 . 0,025 . 12
J = 750
Logo, os juros totais são de R$ 750,00.
b) M = C + J
M = 2500 + 750
M = 3250
Logo, no final da aplicação teremos R$ 3250,00.
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
Um capital de R$ 800,00 foi aplicado a taxa de 18% a.a. por um período de 45 meses a juros simples.
a) Qual o valor total dos juros?
b) Qual o valor total disponível nessa aplicação no final do período?
Resolução
a) A partir do enunciado:
C = 800
i = 18% = 0,18
t = 45 meses ÷ 12 = 3,75 anos
J = C . i . t
J = 800 . 0,18 . 3,75
J = 540
Logo, os juros totais são de R$ 540,00.
b) M = C + J
M = 800 + 540
M = 1340
Logo, no final da aplicação teremos R$ 1340,00.
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
Um capital de R$ 620,00 foi aplicado a juros simples por 18 meses gerando um total de R$ 876,68.
a) Qual o valor total dos juros no período considerado?
b) Qual a taxa mensal da aplicação?
Resolução
a) Do enunciado, temos:
C = 620,00
M = 876,68
t = 18 meses
M = C + J
876,68 = 620,00 + J
J = 876,68 – 620,00
J = R$ 256,68
b) J = C . i . t
256,68 = 620,00 . i . 18
256,68 = 11160 . i
i = 256,68 / 11160
i = 0,023
Logo, a taxa foi de 2,3% a.m.
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
Um capital de R$ 3500,00 foi aplicado a juros simples a uma taxa de 3,5% a.m. resultando em um montante de R$ 6195,00. Qual foi o período da aplicação?
Resolução
Do enunciado, temos:
C = 3500
M = 6195
i = 3,5% a.m. = 0,035
M = C + J
6195 = 3500 + J
J = 6195 – 3500
J = R$ 2695,00
J = C . i . t
2695 = 3500 . 0,035 . t
2695 = 122,5. t
t = 2695 / 122,5
t = 22 meses
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
É um sistema de capitalização em que os juros são recalculados a cada mês (no caso de se trabalhar com uma capitalização mensal). Ou seja, o valor dos juros é calculado com base no montante obtido no mês anterior. Esse sistema é o famoso “juros sobre juros”. É utilizado em aplicações financeiras como, por exemplo, poupança, fundos e bolsa de valores.
Para compreender melhor a lógica, os cálculos e as fórmulas de juros simples, vamos analisar um exemplo que ilustra o fluxo de juros.
Suponhamos os seguintes dados:
Capital: C = R$ 4000
Taxa mensal: i = 5% = 0,05
Tempo: 6 meses
Logo, os juros aplicados mensalmente serão calculados sempre sobre o montante do último mês. A figura a seguir ilustra como serão calculados os juros e o montante a cada mês:
Nos exemplos anteriores sobre fluxo de juros, tanto para juros simples como para juros compostos, utilizamos os mesmos parâmetros: capital de R$ 4000, taxa mensal de 5% e um tempo de 6 meses. Compare os resultados e verifique que os juros finais e o montante, quando utilizado os juros compostos, serão sempre maiores que os dos juros simples:
| Comparação | Juros Simples | Juros Compostos |
|---|---|---|
| Juros totais | R$ 1.200,00 | R$ 1.359,94 |
| Montante | R$ 5.200,00 | R$ 5.359,94 |
Já vimos a fórmula:
M = C + J
Ela é válida tanto para juros simples como para juros compostos. Porém, existem fórmulas específicas para juros compostos:
Em que:
J = juros
C = capital
i = taxa
t = tempo
M= montante
Observação: o tempo (t) deve estar na mesma unidade da taxa (i).
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
Um capital de R$ 2500,00 foi aplicado, a juros compostos, a uma taxa de 2,5% a.m. por um período de 12 meses.
a) Qual o valor total disponível nessa aplicação no final do período?
b) Qual o valor total dos juros?
Resolução
a) Do enunciado, temos:
C = 2500
i = 2,5% = 0,025
t = 12
M = 2500. (1 + 0,025)¹²
M = 2500. 1,025¹²
M = R$ 3.362,22
b) M = C + J
3362,22 = 2500 + J
J = 3362,22 - 2500
J = R$ 862,22
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
Um capital de R$ 800,00 foi aplicado a taxa de 18% a.a. por um período de 45 meses a juros compostos.
a) Qual o valor total disponível nessa aplicação no final do período?
b) Qual o valor total dos juros?
Resolução
a) Do enunciado, temos:
C = 800
i = 18% = 0,18
t = 45 meses ÷ 12 = 3,75 anos
M = R$ 1488,15
b) M = C + J
1488,15 = 800 + J
J = 1488,15 - 800
J = R$ 688,15
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
Um capital de R$ 620,00 foi aplicado a juros compostos por 18 meses gerando um total de R$ 876,68.
a) Qual o valor total dos juros no período considerado?
b) Qual a taxa mensal da aplicação?
Resolução
a) Do enunciado, temos:
C = 620,00
M = 876,68
t = 18 meses
M = C + J
876,68 = 620 + J
J = 876,68 - 620
J = R$ 256,68
b)
i = 1,0194 - 1
i = 0,0194 ou 1,94% a.m.
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
Um capital de R$ 3500,00 foi aplicado a juros compostos a uma taxa de 3,5% a.m. resultando em um montante de R$ 6281,36. Qual foi o período da aplicação?
Resolução
Do enunciado, temos:
C = 3500
M = 6281,36
i = 3,5% a.m. = 0,035
t = 16,99997 ou seja, 17 meses.
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
Você também pode se interessar por:
Cálculo de porcentagens, cálculos e fórmulas de aumentos e descontos percentuais, exemplos resolvidos e lista de exercícios
Vejas todos os conteúdos disponíveis sobre Matemática
Veja todos os conteúdos disponíveis sobre Limites, Derivadas e Integrais