Conrad Elber Pinheiro
Professor Guru
Atualizado em 09/07/2023
Introdução
1. Gráfico de linhas ou em curva
2. Gráfico de colunas
3. Gráfico de barras
4. Gráfico de setores (pizza ou torta)
5. Gráfico de Dispersão
6. Diagrama ramo-e-folhas
7. Pictograma
8. Histograma
9. Polígono de frequência
10. Comparação entre histograma e polígono de frequências
11. Erros comuns na construção de gráficos
12. Enganando com gráficos
13. Lista de Exercícios
Respostas dos Exercícios
Ao final desta página, você pode fazer o download gratuito da apostila sobre Gráficos Estatísticos em formato PDF.
Clique aqui para assistir a playlist com os conteúdos desta página no YouTube
O gráfico estatístico é uma forma de apresentação dos dados estatísticos, cujo objetivo é o de proporcionar, ao leitor, uma visualização mais rápida, e de forma mais agradável e atrativa à maioria das pessoas, do conjunto de dados. Além disso, é uma forma de resumir as informações do conjunto de dados brutos facilitando a leitura e interpretação dos dados. Um bom gráfico estatístico segue as seguintes regras:
- Simplicidade: trazer apenas o essencial; evitar desenhos, etc., que desviem a atenção;
- Clareza: possibilitar a leitura correta dos valores do fenômeno;
- Veracidade: expressar a verdade sobre o fenômeno representado, ou seja, não apresentar distorções na escala, por exemplo, que levem o leitor a interpretar de maneira incorreta o conjunto de dados.
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
O gráfico em linha constitui uma aplicação do processo de representação das funções num sistema de coordenadas cartesianas.
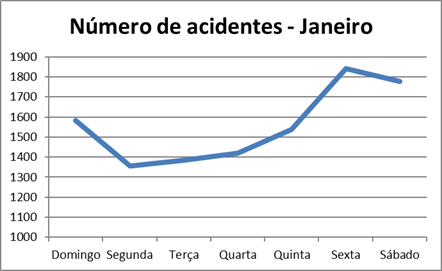
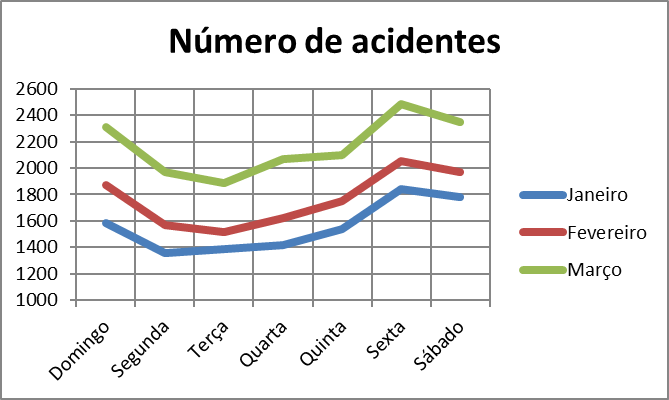
Tabela: Distribuição Mensal dos Acidentes de Trânsito com Vítimas
|
Dia da semana |
Janeiro |
Fevereiro |
Março |
|
Domingo |
1584 |
1872 |
2309 |
|
Segunda |
1356 |
1567 |
1970 |
|
Terça |
1383 |
1518 |
1886 |
|
Quarta |
1418 |
1620 |
2064 |
|
Quinta |
1539 |
1753 |
2098 |
|
Sexta |
1840 |
2054 |
2487 |
|
Sábado |
1777 |
1968 |
2347 |
|
Total |
10897 |
12352 |
15161 |
O gráfico de curva para o mês de janeiro, possibilita uma visão dos dias de maior incidência de acidentes.
Podemos fazer o gráfico poligonal para os três meses juntos.
Observa-se no gráfico que sexta-feira, sábado e domingo são os dias de maior número de acidentes com vítimas, nos três meses.
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
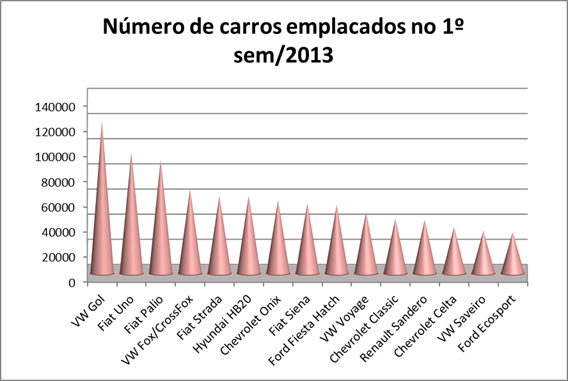
Os gráficos de colunas são, geralmente, utilizados para representar variáveis qualitativas. O gráfico consiste em construir retângulos verticais em que colocamos os valores das variáveis no eixo das abscissas (eixo horizontal ou eixo x) e as frequências observadas no eixo das ordenadas (eixo vertical ou eixo y). Todas as colunas possuem base de mesma largura e geralmente há um espaço vazio entre cada uma das colunas.
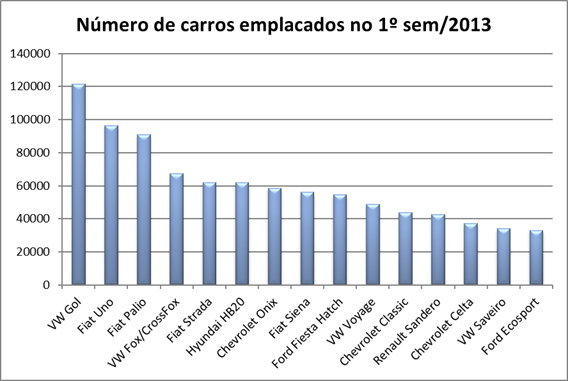
Veja a tabela que nos mostra os carros mais vendidos do Brasil (modelos mais emplacados) de janeiro a junho de 2013, segundo dados da Fenabrave (Federação Nacional da Distribuição de Veículos Automotores):
|
Posição |
CARRO |
JANEIRO |
FEVEREIRO |
MARÇO |
ABRIL |
MAIO |
JUNHO |
TOTAL |
|
1 |
VW Gol |
22337 |
15715 |
19227 |
21581 |
19955 |
22541 |
121356 |
|
2 |
Fiat Uno |
18024 |
11109 |
15235 |
17463 |
18352 |
16326 |
96509 |
|
3 |
Fiat Palio |
17358 |
13130 |
14041 |
16654 |
15474 |
14088 |
90745 |
|
4 |
VW Fox/CrossFox |
12436 |
8595 |
9728 |
11979 |
10626 |
13807 |
67171 |
|
5 |
Fiat Strada |
10204 |
8219 |
9003 |
11745 |
11081 |
11764 |
62016 |
|
6 |
Hyundai HB20 |
9029 |
10178 |
12536 |
12118 |
9631 |
8408 |
61900 |
|
7 |
Chevrolet Onix |
10724 |
9037 |
9408 |
9428 |
10184 |
9743 |
58524 |
|
8 |
Fiat Siena |
9850 |
6820 |
8558 |
10405 |
10748 |
9581 |
55962 |
|
9 |
Ford Fiesta Hatch |
7215 |
5550 |
9139 |
8319 |
11395 |
12995 |
54613 |
|
10 |
VW Voyage |
8024 |
6146 |
8387 |
10635 |
8347 |
7410 |
48949 |
|
11 |
Chevrolet Classic |
8479 |
4581 |
6196 |
7358 |
7881 |
9195 |
43690 |
|
12 |
Renault Sandero |
7357 |
4511 |
5845 |
8968 |
7375 |
8707 |
42763 |
|
13 |
Chevrolet Celta |
9241 |
5421 |
6638 |
6389 |
4389 |
5004 |
37082 |
|
14 |
VW Saveiro |
5925 |
4990 |
6390 |
5073 |
5105 |
6577 |
34060 |
|
15 |
Ford Ecosport |
6367 |
4323 |
4495 |
6397 |
5828 |
5622 |
33032 |
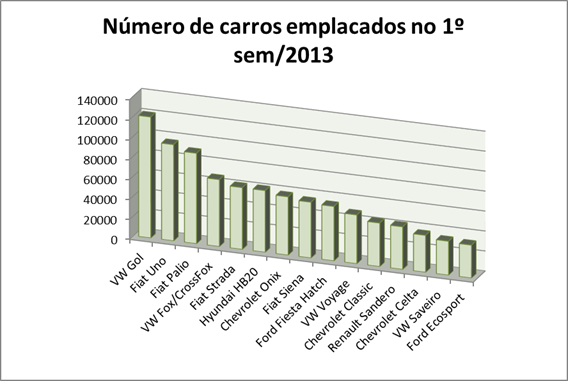
Podemos construir um gráfico de colunas para comparar os totais obtidos. Os gráficos a seguir, representam algumas possibilidades de gráficos que podemos construir a partir de um mesmo conjunto de dados.
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
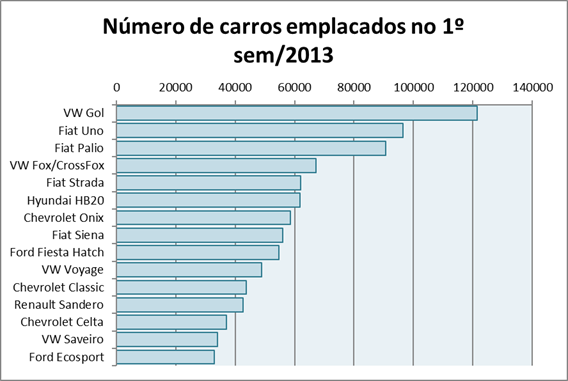
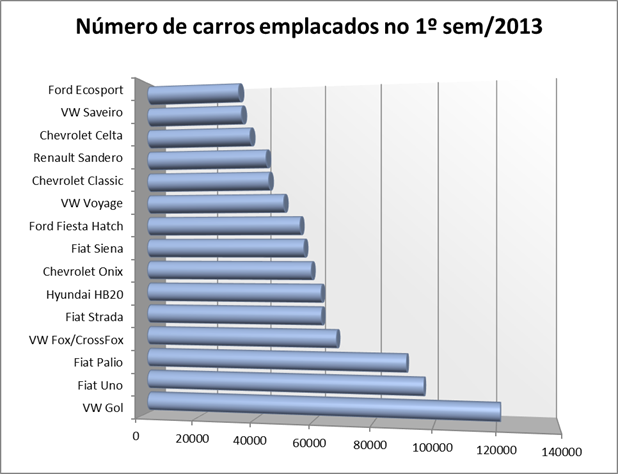
Os gráficos de barras são, geralmente, utilizados para representar variáveis qualitativas. O gráfico consiste em construir retângulos horizontais em que colocamos os valores das variáveis no eixo das ordenadas (eixo vertical ou eixo y) e as frequências observadas no eixo das abscissas (eixo horizontal ou eixo x). Todas as barras possuem altura de mesma largura e geralmente há um espaço vazio entre cada uma das barras.
Podemos construir um gráfico de barras para comparar os totais obtidos. Os gráficos a seguir, representam algumas possibilidades de gráficos que podemos construir a partir de um mesmo conjunto de dados.
Para os exemplos a seguir, considere novamente a tabela apresentada no tópico anterior (gráfico de colunas).
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
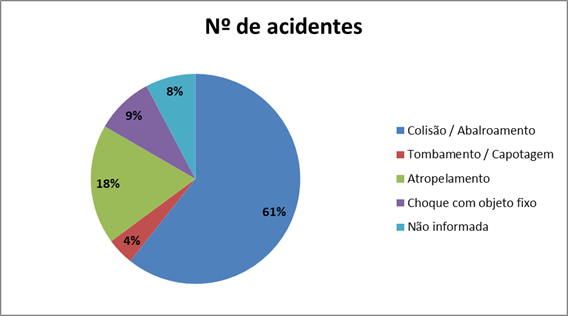
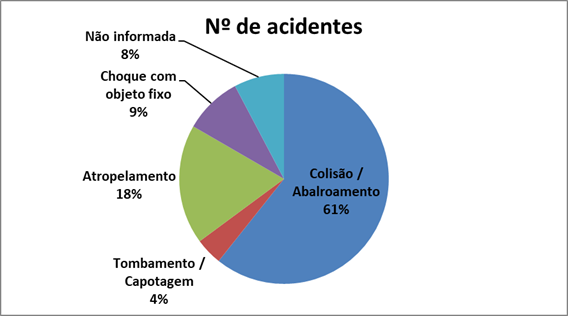
O gráfico de composição em setores, destina-se a representar a composição, usualmente em porcentagem, de partes de um todo. Consiste num círculo de raio arbitrário, representando o todo, dividido em setores, que correspondem às partes de maneira proporcional.
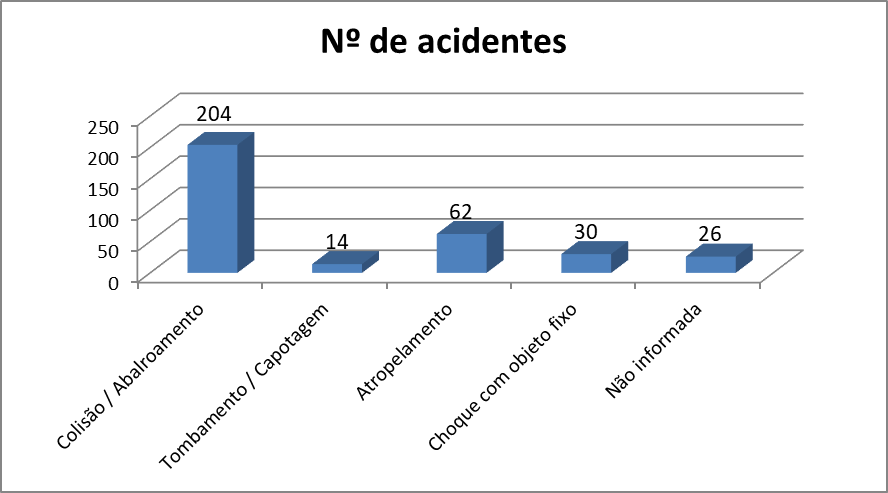
Suponha que um determinado município do interior de SP tenha coletado, ao longo do mês de julho de 2012, o número de acidentes segundo o tipo, conforme mostrado na tabela a seguir:
Tabela: acidentes segundo as categorias
|
Categoria |
Nº de acidentes |
|
Colisão / Abalroamento |
204 |
|
Tombamento / Capotagem |
14 |
|
Atropelamento |
62 |
|
Choque com objeto fixo |
30 |
|
Outra |
0 |
|
Não informada |
26 |
|
Total |
336 |
Considerando a tabela, o gráfico de setores, dos acidentes segundo o tipo, ressalta as diferenças entre as percentagens dos tipos de acidentes.
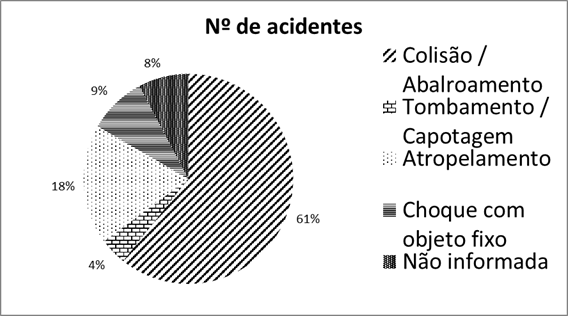
Perceba que no gráfico anterior, caso o gráfico seja impresso em preto e branco, a identificação de cores fica prejudicada. Duas soluções possíveis, para este caso, são a utilização da legenda diretamente nos setores do gráfico ou a utilização de texturas, conforme vemos a seguir.
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
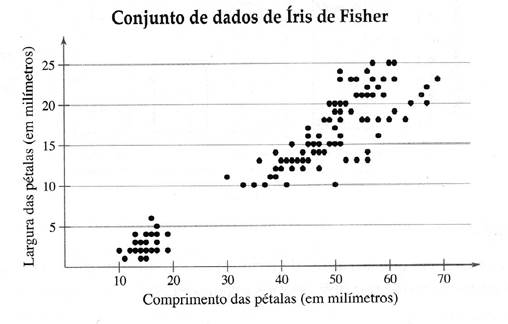
Em um gráfico de dispersão, os pares ordenados dos valores observados são representados como pontos em um plano coordenado. Um gráfico de dispersão é usado para mostrar a relação entre duas variáveis quantitativas.
“O estatístico britânico Ronald Fisher apresentou um famoso conjunto de dados chamado de conjunto de dados de íris de Fisher. Esse conjunto de dados descreve várias características físicas tais como o comprimento de pétalas e a sua largura (em milímetros), para três espécies de íris (flor). No gráfico de dispersão mostrado, os comprimentos de pétalas formam o primeiro conjunto de dados e as larguras formam o segundo conjunto de dados.”
O eixo horizontal representa o comprimento da pétala e o vertical representa a largura da pétala. Cada ponto no gráfico de dispersão representa o comprimento das pétalas e a largura em uma flor. Com base no gráfico de dispersão, você pode ver que, conforme o comprimento da pétala aumenta, a largura também tende a aumentar.
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
Em um diagrama de ramo-e-folhas, cada número é separado em um ramo (por exemplo, as entradas dos dígitos na extremidade esquerda) e uma folha (por exemplo, o dígito mais à direita). Você deve ter tantas folhas quanto entradas no conjunto de dados original. Um diagrama de ramo-e-folhas tem a vantagem de que o gráfico contém os valores originais dos dados. Outra vantagem de um diagrama de ramo-e-folhas é que ele fornece uma maneira rápida de se classificar dados.
A seguir, temos os números de mensagens de texto enviadas no mês passado por usuários de telefonia celular em um andar de um dormitório universitário.
155 159 144 129 105 145 126 116 130 114 122 112 112 142 126
118 118 108 122 121 109 140 126 119 113 117 118 109 109 119
139 139 122 78 133 126 123 145 121 134 124 119 132 133 124
129 112 126 148 147
Em razão de as entradas de dados irem de um número baixo (78) para um número alto (159), você deve usar valores de ramo de 7 a 15. Para construir o diagrama, liste esses ramos à esquerda de uma linha vertical. Para cada entrada de dados, liste uma folha à direita de seu ramo. Por exemplo, a entrada 155 tem um ramo de 15 e uma folha de 5. O diagrama ramo-e-folhas será desordenado. Para obter o diagrama ramo-e-folhas, reescreva o diagrama com folhas em ordem crescente da esquerda para a direita. É importante incluir uma chave para o gráfico para identificar os valores dos dados.
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
O pictograma constitui um dos processos gráficos que melhor fala ao público, pois sua representação gráfica é feita através de figuras. Os pictogramas tem, dentre as suas principais utilizações: apresentações, seminários, jornais, revistas, TV, internet. Ou seja, o maior objetivo de um pictograma é chamar a atenção e prender a atenção dos leitores, ouvintes ou telespectadores.
Note que o gráfico anterior nada mais é do que um gráfico de colunas com os rótulos de colunas (correspondentes às porcentagens). Porém, as colunas foram estilizadas na forma de frascos de remédios: uma forma eficaz de chamar a atenção dos leitores do jornal em que a reportagem foi publicada.
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
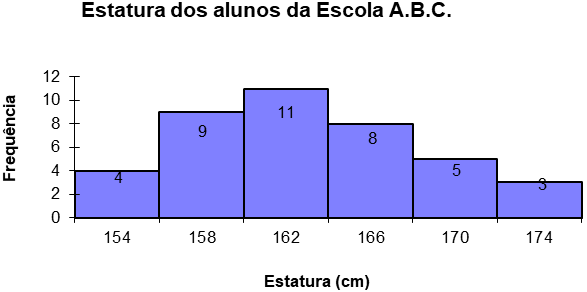
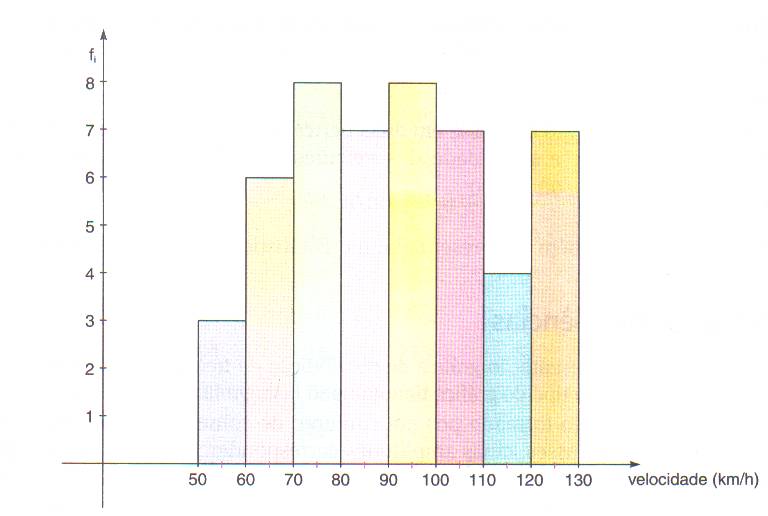
Quando se trata da representação gráfica de distribuição de frequências com dados agrupados utilizamos um gráfico denominado histograma de frequências absolutas.
Histograma é um gráfico de barras contíguas, isto é, formado por um conjunto de retângulos justapostos. No eixo das abscissas (x) marcamos as classes, cujas amplitudes correspondem às bases dos retângulos ou, se preferir, podemos marcar os pontos médios de cada classe. No eixo das ordenadas (y) marcamos as frequências absolutas, que correspondem às alturas dos retângulos. Os pontos médios das bases dos retângulos coincidem com os pontos médios dos intervalos das classes.
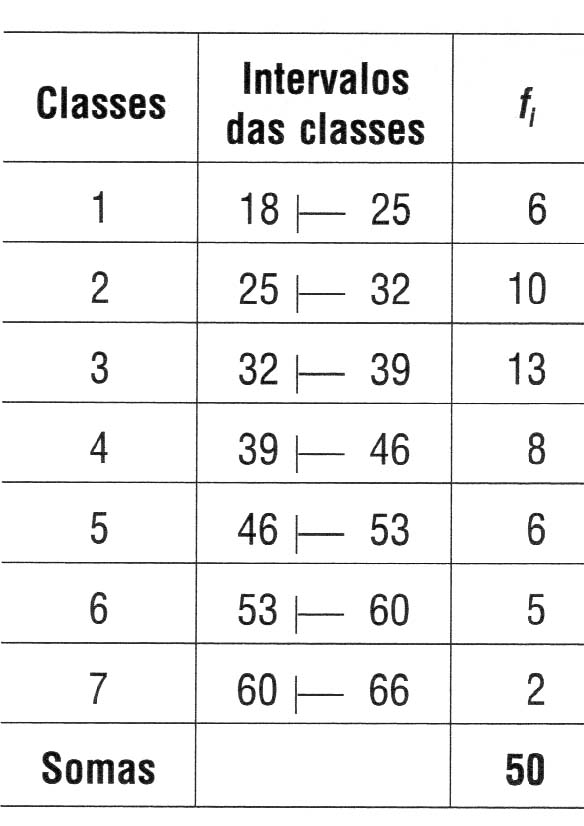
Um radar, instalado num trecho de uma rodovia, registrou as velocidades de 50 veículos. As velocidades, em quilômetros por hora, estão indicadas na tabela de distribuição de frequências:
|
Classe |
Velocidade(km/h) |
fi |
Fi |
fr (%) |
Fr (%) |
|
1 |
[50; 60[ |
3 |
3 |
6 |
6 |
|
2 |
[60; 70[ |
6 |
9 |
12 |
18 |
|
3 |
[70; 80[ |
8 |
17 |
16 |
34 |
|
4 |
[80; 90[ |
7 |
24 |
14 |
48 |
|
5 |
[90; 100[ |
8 |
32 |
16 |
64 |
|
6 |
[100; 110[ |
7 |
39 |
14 |
78 |
|
7 |
[110; 120[ |
4 |
43 |
8 |
86 |
|
8 |
[120; 130[ |
7 |
50 |
14 |
100 |
Construindo o histograma referente aos dadas da tabela temos:
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
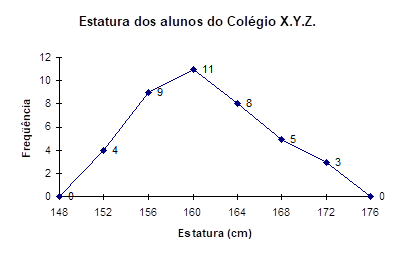
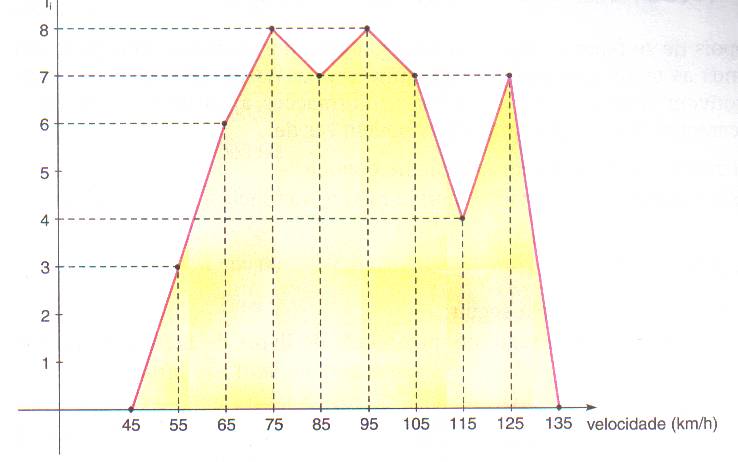
A partir de uma tabela de distribuição de frequências ou histograma é possível construir um polígono de frequências. O polígono de frequência é um gráfico em linha, sendo construído a partir dos pontos médios dos intervalos de classes (eixo das abscissas) e as frequências absolutas (eixo das ordenadas). Unindo os pontos obtidos por meio de segmentos de reta formamos o polígono.
Anteriormente, vimos o seguinte histograma:
Agora, a partir desse histograma, podemos construir o polígono de frequências:
A partir da tabela e do histograma (exemplo 2), em que tratava de um radar, instalado num trecho de uma rodovia, que registrou as velocidades de 50 veículos, podemos construir o polígono de frequências:
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
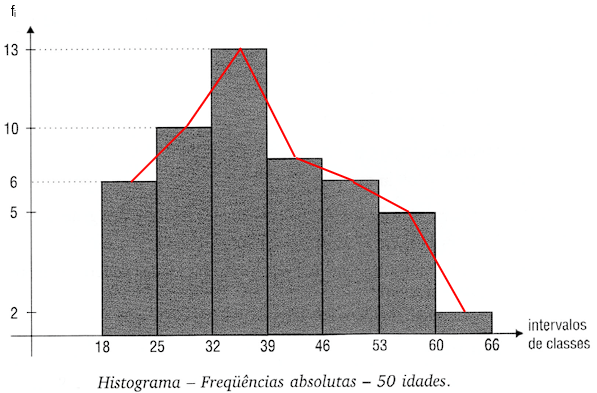
Considere as idades de 50 funcionários de uma empresa, agrupados conforme a tabela a seguir:
Podemos construir um histograma a partir desses dados e, no mesmo gráfico, traçarmos o polígono de frequências (unindo os pontos médios dos topos de cada coluna):
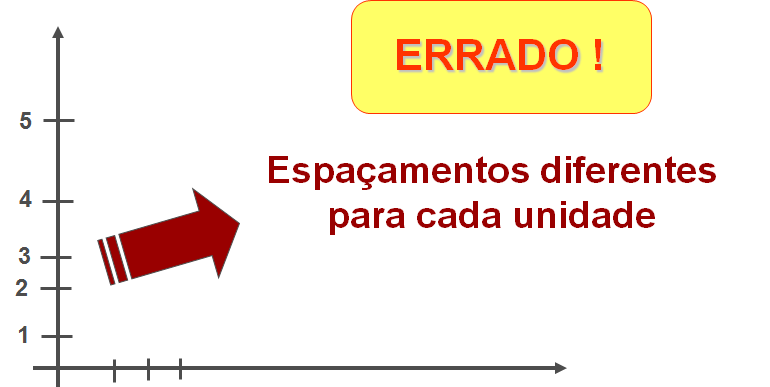
A seguir, vamos ver dois erros muito frequentes na construção de gráficos. Esses erros mais comuns se referem, quase sempre, à construção errada da escala em um ou em ambos eixos.
Neste primeiro gráfico, claramente vemos um erro na escala que, basicamente, se deve ao fato de não ter usado uma régua. Os valores do eixo variam de 1 em 1, porém, a distância entre cada marcação possui variações diferentes.
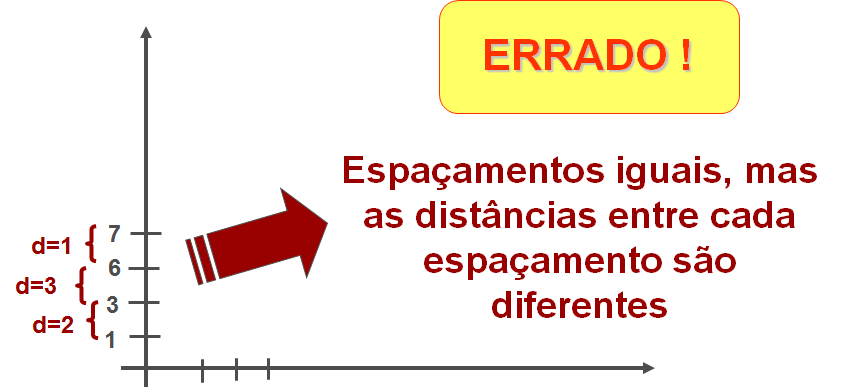
Já neste segundo gráfico, temos o contrário do anterior. Desta vez, foi utilizada uma régua para fazer as marcações no eixo vertical, porém, os valores anotados ao lado de cada marcação possuem variações diferentes. Ou seja, para uma mesma distância entre duas marcações, ora temos uma variação de 2 unidades (de 1 para 3), ora de 3 unidades (de 3 para 6) e ora de 1 unidade (de 6 para 7). Isso é um ERRO na ESCALA do gráfico.
No gráfico a seguir, temos escalas diferentes em cada um dos eixos. Isso está correto. No eixo vertical, temos um espaçamento entre cada marcação que é diferente dos espaçamentos entre marcações do eixo horizontal. E, ainda, entre cada marcação no eixo vertical temos uma variação de 2 unidades, enquanto que no eixo horizontal temos uma variação de 5 unidades.
Isso é normal de acontecer. E pode ser feito, sem problemas! Ou seja, o gráfico a seguir está correto e com escala correta!
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
A ideia de um gráfico é possibilitar a sua leitura correta, ou seja, observar os dados e conseguir interpretá-los com certa precisão (pois depende da escala adotada).
É muito comum algumas pessoas, com o intuito de deixar o trabalho ou apresentação “mais bonitos”, utilizarem recursos como cores e formas tridimensionais. O grande problema é que, fazendo isso, podemos criar ilusões de ótica através dos gráficos, fazendo com que o leitor seja levado ao erro de leitura e interpretação.
Suponha a mesma tabela apresentada anteriormente:
Tabela: acidentes segundo as categorias
|
Categoria |
Nº de acidentes |
|
Colisão / Abalroamento |
204 |
|
Tombamento / Capotagem |
14 |
|
Atropelamento |
62 |
|
Choque com objeto fixo |
30 |
|
Outra |
0 |
|
Não informada |
26 |
|
Total |
336 |
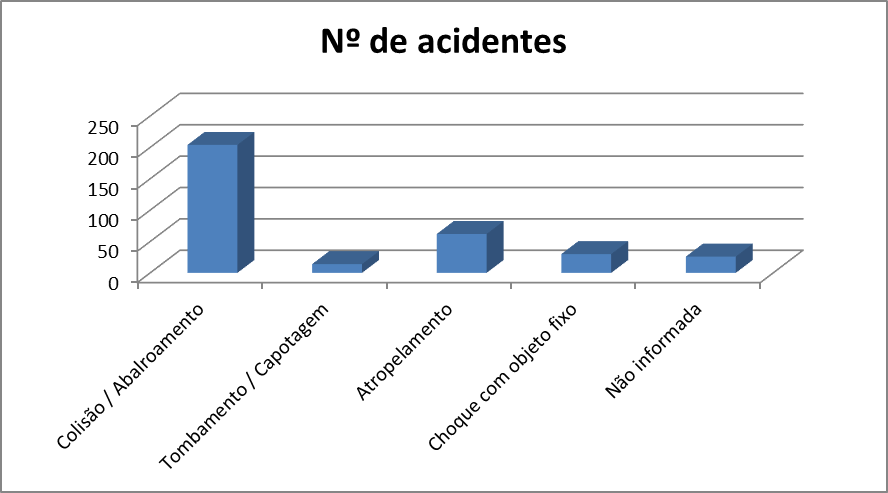
A partir dessa tabela, utilizando o Excel, foi gerado o gráfico de colunas tridimensionais a seguir:
Observe que no gráfico anterior, devido ao efeito 3D, é um pouco complicado percebermos as diferenças absolutas entre as quantidades de acidentes. E, pior ainda, esse gráfico pode nos levar a conclusões falsas.
Perceba que facilmente podemos concluir que a quantidade de colisões / abalroamentos (1ª coluna) foi inferior a 200. Porém, observe o verdadeiro valor na tabela: 204. O gráfico está correto, e nenhum dado foi modificado. O que se fez foi “girar” de maneira adequada a gerar uma ilusão de ótica fazendo com que o leitor acredite que essa coluna possui uma quantidade inferior a 200.
Para “corrigir” esse problema, podemos utilizar, como alternativa, a exibição dos valores acima de cada coluna (no Excel, essa opção é conhecida como rótulo de colunas):
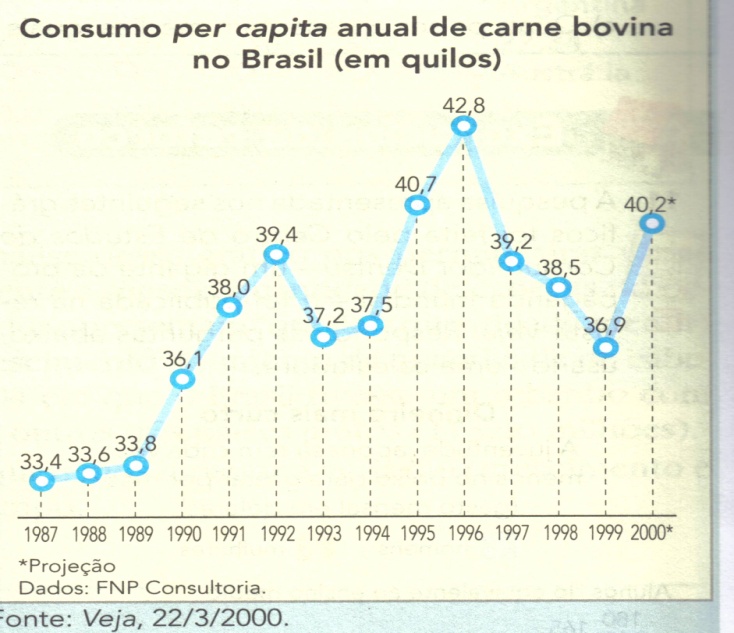
1) O consumo de proteína é um grande indicador de prosperidade. Dados preliminares indicam que cada brasileiro vai consumir, em média, 40 quilos de carne neste ano. A explicação para isso é o crescimento do PIB. O consumo deve aumentar também nas classes mais altas, em que os produtores informam ter havido uma onda anticarne vermelha, que parece ter acabado.
Verdadeiro ou Falso?
a) O consumo per capita foi sempre crescente.
b) O consumo per capita foi crescente de 1987 até 1992.
c) O crescimento percentual entre 1991 e 1992 foi de aproximadamente 3,7%.
d) Entre 1996 e 1997 houve decrescimento de aproximadamente 23%.
e) O consumo foi decrescente entre 1992 e 1999.
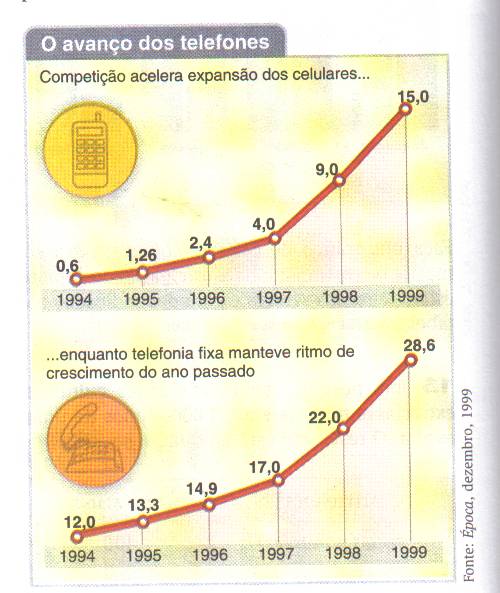
2) Primeiro observe os gráficos, depois responda:
a) Quantos telefones fixos existiam no Brasil em 1994? E celulares?
b) Qual o crescimento percentual desses dois tipos de telefones no período de 97 a 98?
c) Se o crescimento anual do número de celulares seguir o ritmo esperado para o período 98/99, qual a estimativa desse número para o final do ano de 2001?
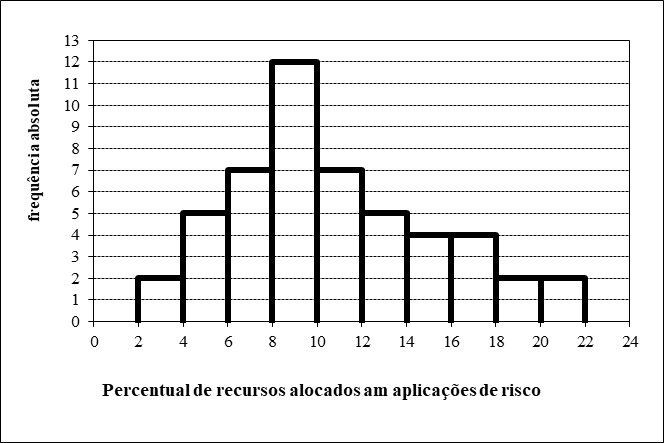
3) Um gerente estava interessado em estudar o percentual de recursos alocados em aplicações de risco, de um conjunto de clientes com recursos acima de R$ 100.000,00. Para tanto, foi selecionada uma amostra de clientes com esse perfil e fez-se o histograma da variável percentual de recursos alocados em aplicações de risco.
a) Quantos clientes foram pesquisados?
b) Qual a porcentagem de clientes que alocaram um percentual de recursos superior a 18 em aplicações de risco.
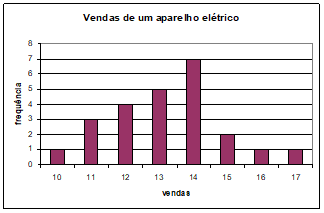
4) A tabela a seguir apresenta as vendas de determinado aparelho elétrico, durante um mês, por uma firma comercial:
|
vendas |
frequência |
|
10 |
1 |
|
11 |
3 |
|
12 |
4 |
|
13 |
5 |
|
14 |
7 |
|
15 |
2 |
|
16 |
1 |
|
17 |
1 |
Apresente os resultados em um gráfico de colunas.
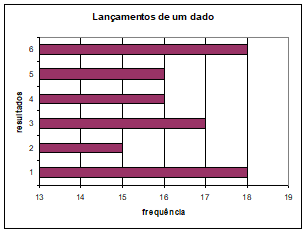
5) Lançou-se um dado 100 vezes, obtendo-se os seguintes resultados:
|
resultado |
frequência |
|
1 |
18 |
|
2 |
15 |
|
3 |
17 |
|
4 |
16 |
|
5 |
16 |
|
6 |
18 |
Apresentar os resultados em um gráfico de barras.
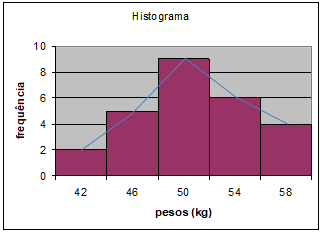
6) Construa o histograma e o polígono de frequência da tabela abaixo:
|
Pesos (kg) |
fi |
|
40 I--- 44 |
2 |
|
44 I--- 48 |
5 |
|
48 I--- 52 |
9 |
|
52 I--- 56 |
6 |
|
56 I---60 |
4 |
|
Total |
26 |
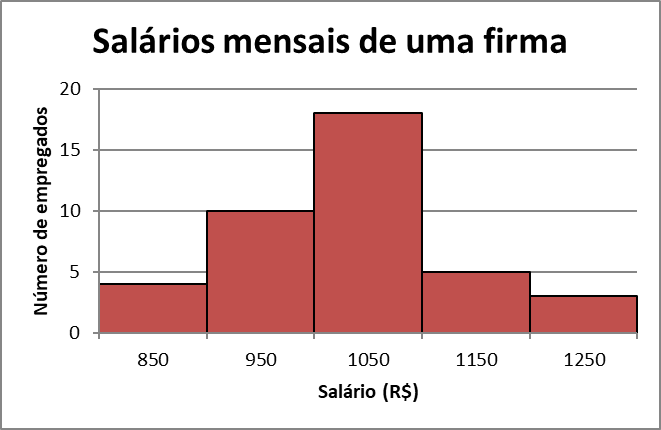
7) O quadro mostra a distribuição dos salários mensais de 40 empregados de uma firma.
|
Salário |
Número de |
|
(em reais) |
empregados |
|
[800, 900[ |
4 |
|
[900, 1 000[ |
10 |
|
[1 000, 1 100[ |
18 |
|
[1 100, 1 200[ |
5 |
|
[1 200, 1 300] |
3 |
Nessa condições:
a) Quantos empregados ganham menos que R$ 1000,00 mensais?
b) Qual o índice, em porcentagem, de empregados que ganham R$ 1000,00 mensais ou mais?
c) Quantos empregados ganham entre R$ 800,00 (inclusive) e R$ 1200,00?
d) Qual o índice, em porcentagem, de empregados que ganham menos que R$1000,00 mensais?
e) Qual é a amplitude do intervalo de classe?
f) Elabore uma tabela de distribuição de frequências acumuladas, relativas e relativas acumuladas.
g) Construa o histograma de frequências.
8) No quadro a seguir estão registradas as massa, em quilograma, de 50 pessoas que frequentam uma academia de ginástica.
|
72 |
81 |
57 |
64 |
87 |
90 |
74 |
69 |
77 |
73 |
|
80 |
96 |
55 |
58 |
88 |
92 |
47 |
60 |
68 |
80 |
|
77 |
76 |
59 |
57 |
83 |
81 |
90 |
68 |
65 |
74 |
|
91 |
97 |
86 |
82 |
73 |
64 |
69 |
71 |
88 |
94 |
|
77 |
72 |
81 |
91 |
49 |
75 |
52 |
50 |
63 |
70 |
a) Faça uma tabela de distribuição de frequências absolutas e relativas. Utilize classes de amplitude 10 e limite inferior da primeira classe igual a 40.
b) Construa o histograma para a distribuição.
c) Calcule os pontos médios dos intervalos e represente a distribuição por meio de um polígono de frequências.
d) Represente essa distribuição por meio de um gráfico de setores.
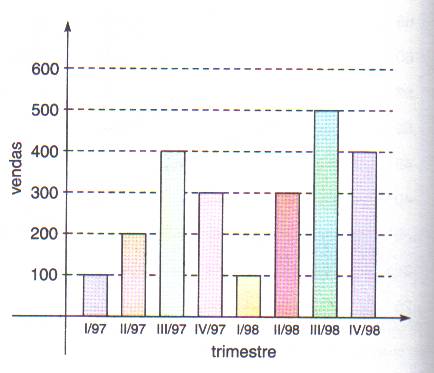
9) O gráfico abaixo fornece o número de unidades vendidas de um produto em função do tempo (dados trimestrais):
a) Qual o aumento percentual de unidades vendidas do quarto trimestre de 1998 (IV/98) em relação ao mesmo período do ano anterior (IV/97)?
b) Qual o aumento percentual de unidades vendidas do ano de 1998 em relação as do ano de 1997?
10) Em uma pesquisa eleitoral para verificar a posição de três candidatos a prefeito de uma cidade, 2000 pessoas foram consultadas. Se o resultado da pesquisa deve ser mostrado em três setores circulares de um mesmo disco e certo candidato recebeu 250 intenções de voto, qual é o ângulo central correspondente a este candidato?
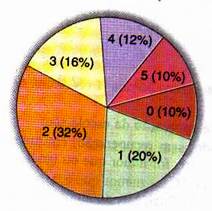
11) O gráfico em forma de pizza representa as notas obtidas em uma questão pelos 32000 candidatos presentes à primeira fase de uma prova de vestibular. Ele mostra, por exemplo, que 32% desses candidatos tiveram nota 2 nessa questão. Construa uma tabela de frequências absolutas e relativas para essa distribuição.
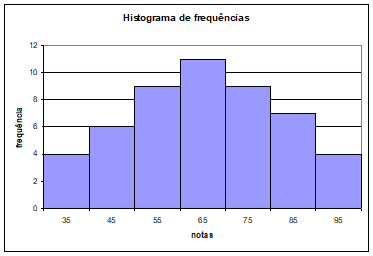
12) As notas de 50 alunos foram agrupadas em classes conforme a tabela:
|
Notas |
fi |
fri |
Fi |
Fri |
Ponto médio (xi) |
|
30 |- 40 |
4 |
|
|
|
|
|
40 |- 50 |
6 |
|
|
|
|
|
50 |- 60 |
9 |
|
|
|
|
|
60 |- 70 |
11 |
|
|
|
|
|
70 |- 80 |
9 |
|
|
|
|
|
80 |- 90 |
7 |
|
|
|
|
|
90 |- 100 |
4 |
|
|
|
|
|
Total |
50 |
|
|
|
|
a) Complete a tabela.
b) Qual a amplitude total?
c) Qual a amplitude de classe?
d) Construa um histograma.
13) Uma pesquisa sobre a idade, em anos de uma classe de calouros de uma faculdade, revelou os seguintes valores:
|
18 |
17 |
18 |
20 |
21 |
19 |
20 |
18 |
17 |
19 |
|
20 |
18 |
19 |
18 |
19 |
21 |
18 |
19 |
18 |
18 |
|
19 |
19 |
21 |
20 |
17 |
19 |
19 |
18 |
18 |
19 |
|
18 |
21 |
18 |
19 |
19 |
20 |
19 |
18 |
19 |
20 |
|
18 |
19 |
19 |
18 |
20 |
20 |
18 |
19 |
18 |
18 |
Determine as frequências absolutas relativas, frequências acumuladas e frequências acumuladas relativas.
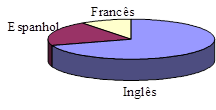
14) Numa escola, os alunos devem optar por um, e somente um, dos três idiomas: inglês, espanhol ou francês. A distribuição da escolha de 180 alunos está indicada pelo gráfico a seguir. Sabendo que o ângulo do setor representado pelos alunos que escolheram inglês é 252º e que apenas 18 alunos optaram por estudar francês, determine:
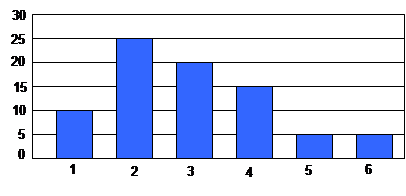
15) (FGV-SP) No gráfico abaixo está representado, no eixo das abscissas (eixo horizontal), o número de fitas de vídeos alugadas por semana numa videolocadora, e no eixo das ordenadas (eixo vertical) a correspondente frequência (isto é, a quantidade de pessoas que alugaram os correspondentes números de fitas):
a) Qual a porcentagem de pessoas que alugaram 4 ou mais fitas?
b) Se cada fita for alugada por R$ 4,00, qual a receita semanal da videolocadora?
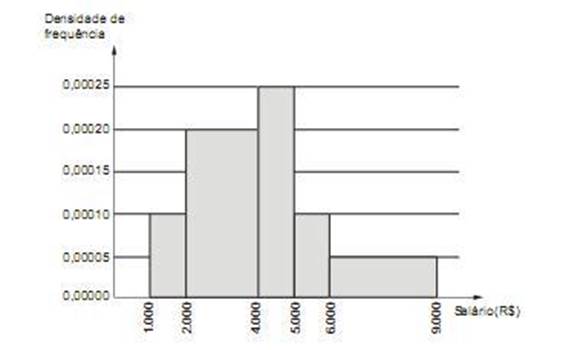
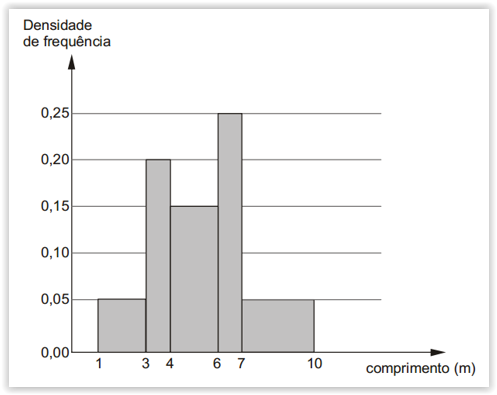
16) (FCC-2012) Considere que a distribuição dos salários dos funcionários em um setor público está representada por um histograma conforme abaixo, em que no eixo vertical constam as densidades de frequências, em (R$)⁻¹. Densidade de frequência de um intervalo de classe é o resultado da divisão da respectiva frequência relativa pela correspondente amplitude do intervalo.
Considerando que todos os intervalos de classes são fechados à esquerda e abertos à direita, a porcentagem P dos funcionários que ganham no mínimo R$ 2.000,00 e menos que R$ 6.000,00 é tal que
a) P ≤ 65%.
b) 65% < P ≤ 70%.
c) 70% < P ≤ 75%.
d) 75% < P ≤ 80%.
e) P > 80%.
17) Observe o gráfico a seguir e responda:
a) Em qual, dos cinco lugares citados, ocorreu o menor prejuízo no software apresentado no gráfico?
b) Quantos bilhões de dólares foram tidos em prejuízos na Europa?
c) Se admitirmos que metade dos prejuízos ocorridos na América Latina foram correspondentes ao Brasil, qual o valor, em milhões de dólares, de prejuízos no Brasil?
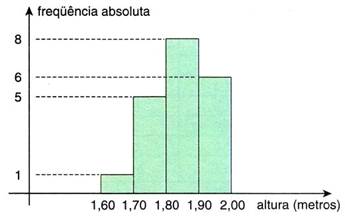
18) O histograma abaixo mostra a altura de 20 atletas de uma equipe de natação.
Podemos concluir que a porcentagem de atletas com altura maior ou igual a 1,80m é:
a) 50%
b) 55%
c) 68%
d) 70%
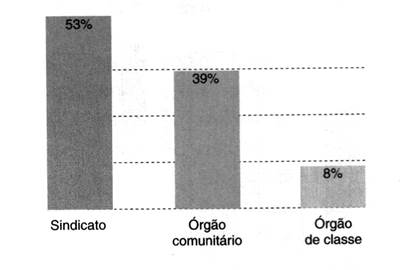
19) Considere os seguintes dados, obtidos em 1996 pelo censo do IBGE, relativo a pessoas maiores de 18 anos filiadas a sindicatos, órgãos comunitários e órgãos de classe (o gráfico indica a porcentagem de pessoas filiadas):
Sabe-se que o número total de pessoas com idade de 18 a 49 anos, nesse censo, era de 73.644.508 pessoas. A partir dos dados acima, pode-se afirmar que o número de pessoas, maiores de 18 anos, filiadas a órgãos comunitários é, aproximadamente, em milhões:
a) 2,87 b) 2,52 c) 29,0 d) 28,7
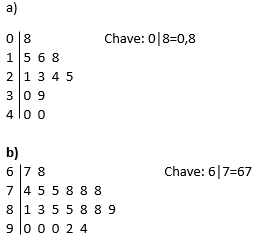
20) Dados os diagramas ramo–e–folhas a seguir, liste, na forma de rol, todo o conjunto de dados apresentado:
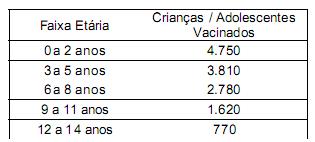
21) (CEPERJ) Considere o quadro abaixo, que apresenta o número de crianças e adolescentes vacinados no 1º semestre de 2006, por faixa etária.
Uma maneira correta de se apresentar estes dados através de um gráfico de colunas é:
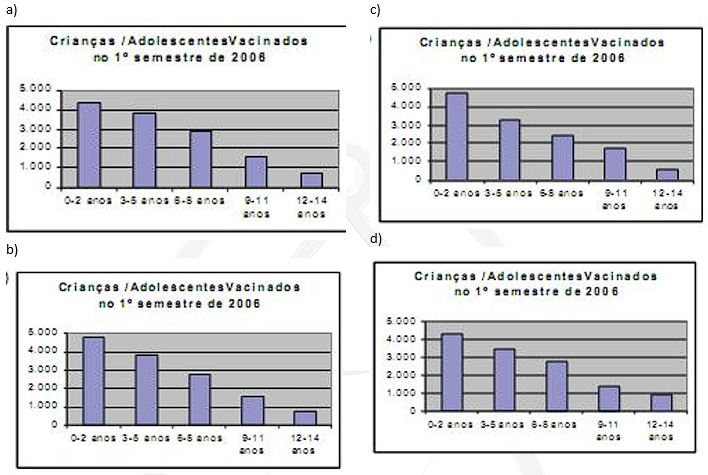
22) (CESGRANRIO) Para responder a questão, utilize os dados do gráfico a seguir, relativos à Avaliação Trienal dos cursos e programas de pós-graduação realizada pela Capes em 2007.
O percentual de programas que tiveram conceito mínimo igual a 4,0 é
a) 15,0%.
b) 28,5%.
c) 32,0%.
d) 34,6%.
e) 65,3%.
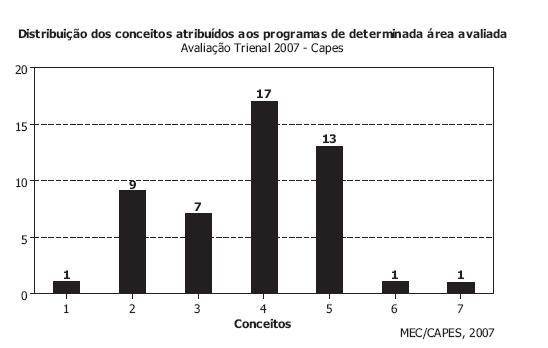
Utilize o gráfico a seguir para responder as questões 23 e 24.
23) (CESGRANRIO) A variação percentual total do número de bolsas de mestrado concedidas pela Capes nesse período de oito anos foi
a) -14.4%.
b) - 8.8%.
c) 0,0%.
d) + 8,8%.
e) + 14,4%.
24) (CESGRANRIO) A amplitude do número de bolsas de doutorado oferecidas pela Capes nesse período foi
a) 672.
b) 1.280.
c) 1.298.
d) 2.204.
e) 2.443.
25) A distribuição das medidas dos comprimentos, em metros (m), dos 400 cabos, em estoque, de uma empresa, está representada pelo histograma abaixo. No eixo das ordenadas constam as respectivas densidades de frequências, em m⁻¹. Densidade de frequência de um intervalo de classe é o resultado da divisão da respectiva frequência relativa pela correspondente amplitude do intervalo.
Considerando que os intervalos de classe são fechados à esquerda e abertos à direita, calcule a quantidade de cabos que possuem um comprimento de, pelo menos, 4m e inferior a 7m.
1) a) F b) V c) V d) F e) F
2) a) 12 milhões de fixos e 600 mil celulares
b) celular: 125%; fixos: 29,4%
c) 27 milhões
3) a) 50 b) 8%
4)
5)
6)
7) a) 14 b) 65% c) 37 d) 35% e) 100 f)
|
Salário (em reais) |
Número de empregados (fi) |
fri |
Fi |
Fri |
|
[800, 900[ |
4 |
10% |
4 |
10% |
|
[900, 1 000[ |
10 |
25% |
14 |
35% |
|
[1 000, 1 100[ |
18 |
45% |
32 |
80% |
|
[1 100, 1 200[ |
5 |
12,5% |
37 |
92,5% |
|
[1 200, 1 300] |
3 |
7,5% |
40 |
100% |
g)
8)
|
Massa (kg) |
fi |
Pt.médio |
fri |
Fi |
Fri |
Ângulo em graus do gráfico de setores |
|
40 |-- 50 |
2 |
45 |
4% |
2 |
4% |
14,4° |
|
50 |-- 60 |
7 |
55 |
14% |
9 |
18% |
50,4° |
|
60 |-- 70 |
9 |
65 |
18% |
18 |
36% |
64,8° |
|
70 |-- 80 |
13 |
75 |
26% |
31 |
62% |
93,6° |
|
80 |-- 90 |
11 |
85 |
22% |
42 |
84% |
79,2° |
|
90 |-- 100 |
8 |
95 |
16% |
50 |
100% |
57,6° |
|
total |
50 |
-- |
100% |
-- |
-- |
360° |
9) a) 33,33% b) 30% c) ângulo central = 156 graus para 1997 e igual a 204 graus para 1998.
10) 45°
11)
|
nota |
fi |
fri |
|
0 |
3200 |
10% |
|
1 |
6400 |
20% |
|
2 |
10240 |
32% |
|
3 |
5120 |
16% |
|
4 |
3840 |
12% |
|
5 |
3200 |
10% |
|
total |
32000 |
100% |
12) a)
|
Notas |
fi |
fri |
Fi |
Fri |
Ponto médio |
|
30 |- 40 |
4 |
0,08 |
4 |
0,08 |
35 |
|
40 |- 50 |
6 |
0,12 |
10 |
0,20 |
45 |
|
50 |- 60 |
9 |
0,18 |
19 |
0,38 |
55 |
|
60 |- 70 |
11 |
0,22 |
30 |
0,60 |
65 |
|
70 |- 80 |
9 |
0,18 |
39 |
0,78 |
75 |
|
80 |- 90 |
7 |
0,14 |
46 |
0,92 |
85 |
|
90 |- 100 |
4 |
0,08 |
50 |
1,00 |
95 |
|
Total |
50 |
1,00 |
-- |
-- |
-- |
b) 100-30 = 70
c) 10
d)
13)
|
Idade (anos) xi |
Nº de alunos (fi) |
fri |
Fi |
Fri |
|
17 |
3 |
0,06 |
3 |
0,06 |
|
18 |
18 |
0,36 |
21 |
0,42 |
|
19 |
17 |
0,34 |
38 |
0,76 |
|
20 |
8 |
0,16 |
46 |
0,92 |
|
21 |
4 |
0,08 |
50 |
1,00 |
|
Total |
50 |
1,00 |
- |
- |
14) a) 36º b) 36 alunos e 72º
15) a) 31,25% b) R$ 940,00
16) C
17) a) Ásia
b) 5,85 bilhões de dólares
c) 675 milhões de dólares
18) D
19) D
20) a) 0,8 1,5 1,6 1,8 2,1 2,3 2,4 2,5 3,0 3,9 4,0 4,0
b) 67, 68, 74, 75, 75, 78, 78, 78, 81, 83, 85, 85, 88, 88, 89, 90, 90, 90, 92, 94
21) B
22) E
23) B
24) A
25) 220 cabos
Faça o download gratuito da apostila sobre Gráficos Estatísticos em formato PDF.
Baixe AgoraVocê também pode se interessar por:
Noções gerais sobre o que é a Estatística, conceitos de população e amostra, variáveis estatísticas (nominal, ordinal, discreta e contínua), técnicas amostragem, arredondamento de números e lista de exercícios
ROL, tabelas de frequências, classes (intervalos), determinação do número de classes em uma tabela, Regra de Sturges e lista de exercícios
Fórmulas e cálculos da média, moda e mediana e lista de exercícios