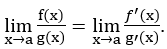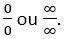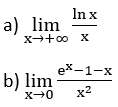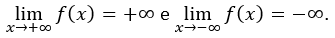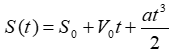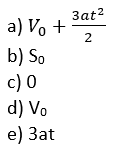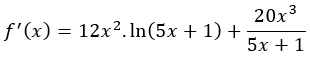Conrad Elber Pinheiro
Professor Guru
Atualizado em 02/08/2023
Clique aqui para assistir a playlist com os conteúdos desta página no YouTube
A seguir, você encontrará uma lista de exercícios contendo Limite usando a Regra de L'Hospital, problemas de otimização, construção de gráfico usando derivadas e limites, Regra da Cadeia e do Produto, ponto de máximo, ponto de mínimo e ponto de inflexão. Todos os exercícios estão resolvidos em vídeo.
Um importante teorema do cálculo é conhecido como Regra de L’Hospital: se f e g são funções contínuas num ponto x=a, em volta do qual
A Regra de L’Hospital é utilizada quando temos indeterminações do tipo
Utilizando esse teorema, calcule os limites a seguir:
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
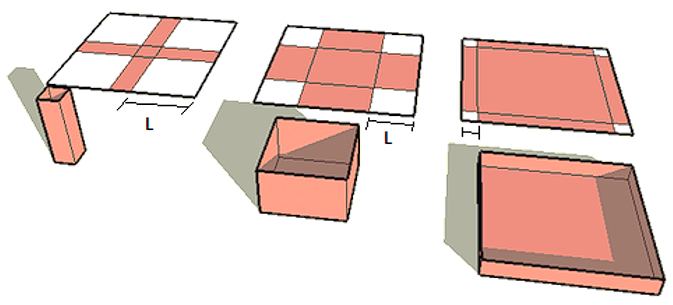
Se se quisesse fazer uma caixa com uma folha de papel quadrada de 24cm de lado seria necessário recortar os quatro cantos dessa folha. Esse corte teria o formato quadrado de tamanho L, para que os lados da caixa tivessem a mesma altura. Para cada L diferente teremos um volume diferente. Abaixo há alguns exemplos de folhas com os cantos recortados:
a) Calcule o valor de L para que o volume da caixa seja máximo. Utilize conceitos de derivadas na resolução.
b) Utilizando o resultado do item a, calcule o volume máximo dessa caixa.
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
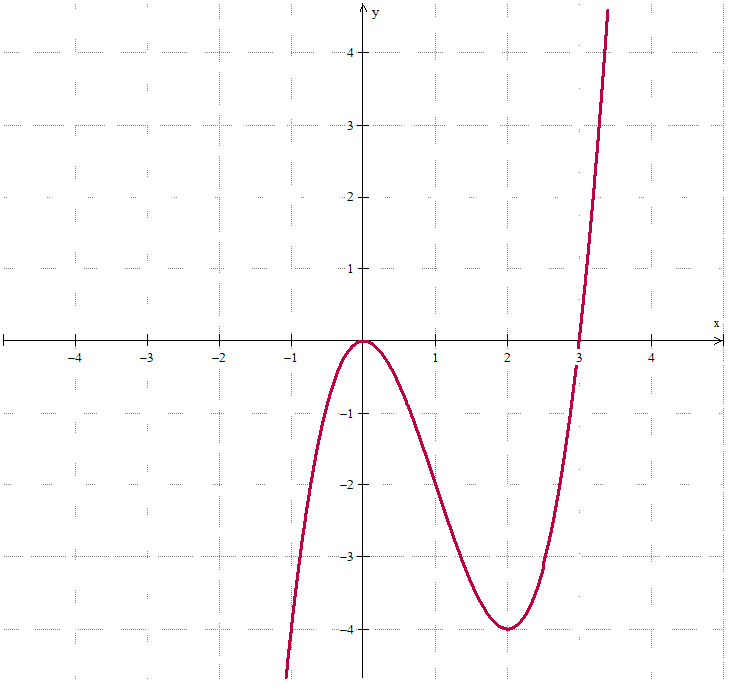
Considere a função f(x) = x³ – 3x² definida no conjunto dos reais.
a) As raízes de uma função são importantes para a construção de um gráfico, visto que elas correspondem aos pontos em que o gráfico cruza o eixo das abscissas (x). Obtenha as raízes reais da função f(x) dada.
b) Calcule a primeira derivada de f(x) e, a partir do estudo do sinal de f’(x), faça o estudo do crescimento e decrescimento da função f(x).
c) Calcule a segunda derivada de f(x) e, a partir do estudo do sinal de f’’(x), faça o estudo das concavidades (para cima ou para baixo) da função f(x).
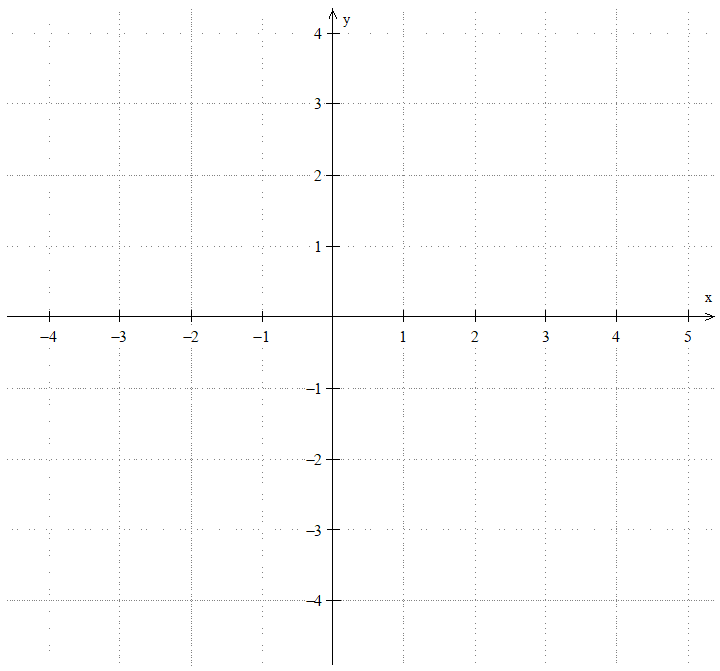
d) Construa o gráfico da função f(x) utilizando o par de eixos a seguir e usando os resultados obtidos nos itens anteriores. Sabe-se, ainda, que
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
Utilizando a Regra da Cadeia e a Regra do Produto, calcule a primeira derivada da função f(x) = 4x³ . ln(5x+1).
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
Considere a função f(x) = x³ – 3x² – 9x + 1. São feitas as afirmações:
I. x = 3 é um ponto de mínimo local.
II. x = –1 é um ponto de máximo global.
III. x = 1 é um ponto de inflexão.
Estão corretas:
a) apenas uma das afirmações.
b) apenas I e II.
c) apenas II e III.
d) apenas I e III.
e) todas as afirmações.
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
A derivada com relação ao tempo da função horária do espaço fornece a expressão da velocidade. A derivada da velocidade fornece a expressão da aceleração. Essas afirmações constam em livros de cálculo e física. Assim, sabendo que expressão da função horária do espaço é
em que S₀, V₀ e a são constantes reais, a expressão da aceleração será:
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
Funções polinomiais possuem diversas aplicações práticas na agricultura, nas ciências ambientais e ciências econômicas. Seja a função polinomial f(x) = x³ – 6x² + 9x + 4. A respeito dessa função, considere as afirmações:
I. A função é decrescente no intervalo 1≤x≤3.
II. A função não admite ponto de máximo global.
III. Em x=2 encontramos um ponto de inflexão.
IV. Considerando o intervalo 0≤x≤2, a função admite um máximo local em x=1.
Quantas das afirmações estão corretas?
a) 0
b) 1
c) 2
d) 3
e) 4
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
Seja a função
O valor da primeira derivada de f(x) calculada no ponto a corresponde ao valor de f'(a) que é igual a:
a) 2.
b) 1.
c) 0.
d) a.
e) 2a.
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
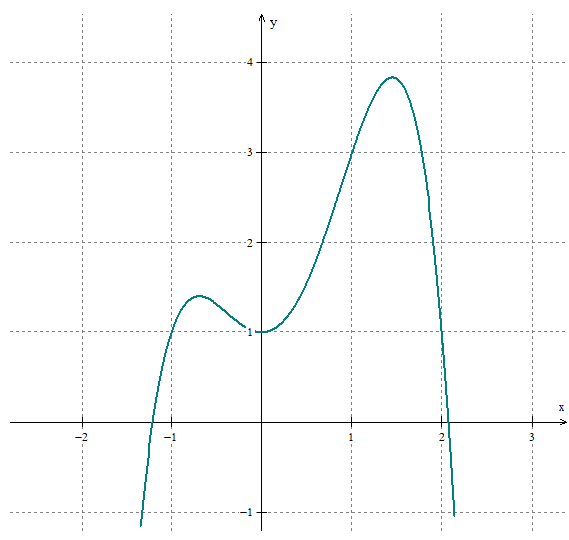
O gráfico de f(x) = –x⁴ + x³ + 2x² + 1 está mostrado a seguir:
Baseado nessas informações, considere as seguintes afirmações:
I. A função f(x) possui duas raízes reais.
II. A função apresenta um ponto de mínimo global em x=0.
III. Dentro do intervalo [1,2], a função possui um ponto de máximo global.
IV. A função f(x) possui três pontos críticos.
V. A função f(x) possui dois pontos de inflexão.
Quantas das afirmações anteriores estão corretas?
a) 1
b) 2
c) 3
d) 4
e) 5
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
A Cia. Gama Ltda. produz um determinado produto e vende–o com um lucro total dado por L(q)= –q³+12q²+60q–4, onde q representa a quantidade produzida. Qual é o valor do lucro máximo?
a) 2796
b) 1596
c) 796
d) 156
e) 84
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
1) a) 0 b) 1/2
2) a) L = 4 cm b) 1024 cm³
3) a) 0 e 3
b) crescente: ]-;0[ e ]2;+[
decrescente: [0;2]
c) concavidade para baixo se x≤1
concavidade para cima de x>1
d)
4)
5) D
6) D
7) E
8) B
9) D
10) C
Você também pode se interessar por:
Veja todos os conteúdos disponíveis sobre Limites, Derivadas e Integrais
Crescimento e decrescimento de funções utilizando a 1ª derivada, pontos críticos, concavidades de funções usando a 2ª derivada, pontos de inflexão
Lista de exercícios com resolução em vídeo envolvendo problemas de otimização, também conhecido como problemas de máximos e mínimos, através do uso de derivadas