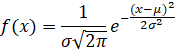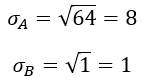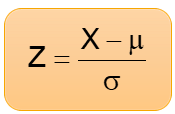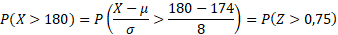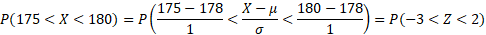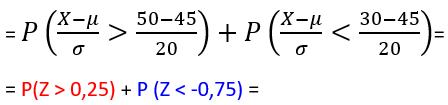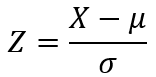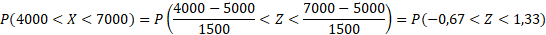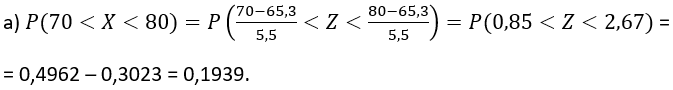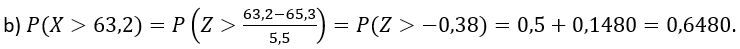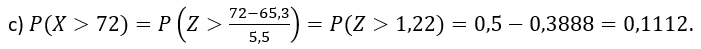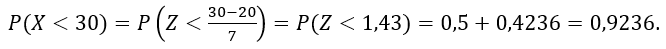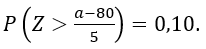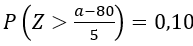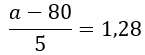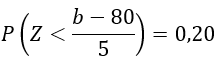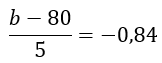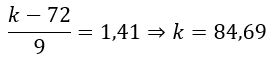Conrad Elber Pinheiro
Professor Guru
Atualizado em 28/07/2023
1. Função Densidade de Probabilidade
2. Distribuição Normal
3. Função densidade de probabilidade da distribuição Normal
4. Propriedades da Normal
5. Área sob a Curva Normal
6. Normal Padrão
7. Usando a tabela da Normal Padrão
Leitura da Tabela da Normal Padrão
8. Resumo das Propriedades da Distribuição Normal
Tabela da Normal Padrão
9. Exemplos Resolvidos - Normal Padrão
10. Lista de Exercícios
Respostas dos Exercícios
Ao final desta página, você pode fazer o download gratuito da apostila sobre Distribuição Normal em formato PDF.
Clique aqui para assistir a playlist com os conteúdos desta página no YouTube
Como já vimos, uma variável aleatória pode ser discreta ou contínua. Quando a variável é contínua, ou seja, assume valores em intervalos da reta dos números reais, a distribuição de frequência de uma amostra de observações pode ser representada através de um histograma.
Agora, porém, queremos analisar a população de onde foi retirada essa amostra. Como não temos acesso ao histograma de frequências relativo à população, não conseguimos determinar, diretamente, o cálculo de qualquer probabilidade. Para o cálculo exato, necessitamos de um modelo para a distribuição de frequências da população. Estudaremos, aqui, dois dos principais modelos contínuos: a Normal e a Exponencial.
Os modelos que serão analisados representam comportamentos de uma extensa série de variáveis do mundo dos negócios e também distribuições teóricas de probabilidades que são fundamentais para os métodos de inferência estatística. Tais modelos são expressos por funções matemáticas denominadas funções densidade de probabilidade.
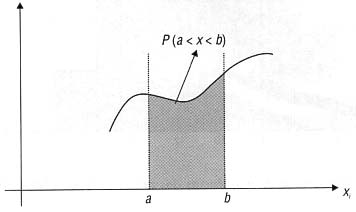
A área sob a curva que expressa a função densidade de probabilidade é igual a 1 (total das probabilidades), sendo que a probabilidade de uma particular observação pertencer a um intervalo é dado pela área sob a curva, correspondente ao intervalo, conforme podemos observar na figura seguinte:
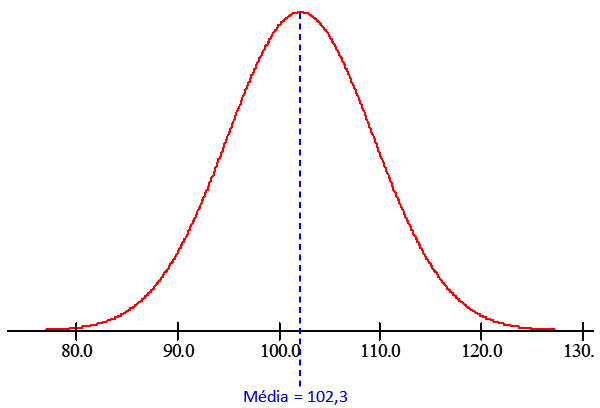
“O mundo é normal!” Acredite se quiser! Muitos dos fenômenos aleatórios que encontramos na prática apresentam uma distribuição muito peculiar, chamada Normal.
Um modelo probabilístico é aquele que nos diz, ou melhor, nos traduz na forma de números o comportamento de uma variável. Por exemplo, já fizemos algumas análises das variáveis altura e peso. Considerando o caso de grandes amostras aleatórias ou mesmo da população, tanto o peso como a altura têm um comportamento muito parecido. Vejamos, por exemplo, a variável altura, considerando-se o sexo masculino e sendo a população os habitantes do Brasil. Essa variável é dita Normal, conforme discutiremos mais adiante.
Essa distribuição de frequência denominada curva normal, considerada um modelo teórico ou ideal que resulta muito mais de uma equação matemática do que de um real delineamento de pesquisa com coleta de dados.
A curva normal é um tipo de curva simétrica, suave, cuja forma lembra um sino. Ela é unimodal, sendo seu ponto de frequência máxima situado no meio da distribuição, em que a média, a mediana e a moda coincidem.
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
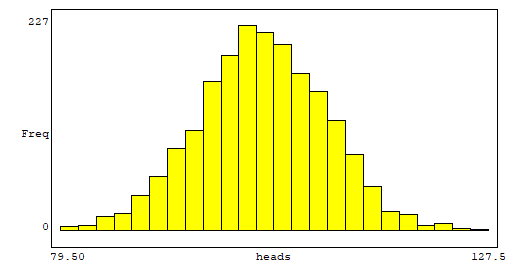
Para exemplificarmos, suponhamos 2000 lançamentos de 200 moedas honestas. Utilizando um software de simulação, obtivemos os seguintes resultados:
[80 ... 81] 5
[82 ... 83] 6
[84 ... 85] 16
[86 ... 87] 19
[88 ... 89] 39
[90 ... 91] 60
[92 ... 93] 91
[94 ... 95] 111
[96 ... 97] 165
[98 ... 99] 194
[100 ... 101] 227
[102 ... 103] 220
[104 ... 105] 206
[106 ... 107] 174
[108 ... 109] 155
[110 ... 111] 123
[112 ... 113] 84
[114 ... 115] 49
[116 ... 117] 21
[118 ... 119] 18
[120 ... 121] 6
[122 ... 123] 8
[124 ... 125] 2
[126 ... 127] 1
sample mean = 102.132
sample st dev = 7.238
A partir desses dados, construímos o histograma:
Observando tal histograma e a tabela anterior, notamos que a média está entre as duas classes com maiores frequências. Além disso, considerando-se a média, percebemos que o histograma parece ser simétrico ao redor dela. A frequência é menor quanto mais nos afastamos da média, tanto para mais quanto para menos, sendo que as menores frequências ocorrem nas pontas do gráfico.
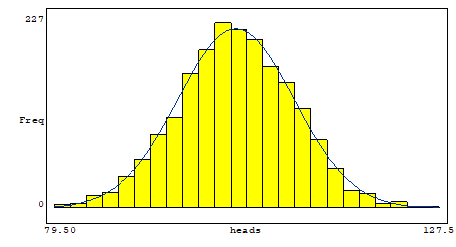
Note que quanto mais classes usamos, mais fácil fica identificarmos um formato criado pelas colunas do histograma. Esse formato faz lembrar um sino, conforme a figura seguinte:
“Limpando” o gráfico acima, temos:
Essa curva que chamamos de sino recebe um nome especial: Curva Normal.
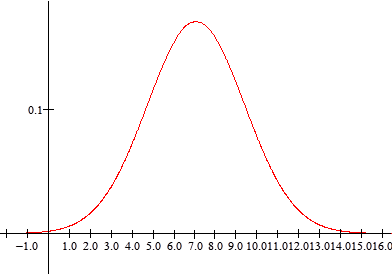
A Curva Normal é a representante do modelo normal e é obtida a partir da função densidade que nada mais é do que uma função que origina o gráfico anterior.
Assim, se X é uma variável aleatória com distribuição Normal com média μ e variância σ² (notação: X ~ N(μ , σ²)) então a sua função densidade é dada por
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
A Normal apresenta as seguintes propriedades:
- é simétrica ao redor da média;
- a área sobre a curva é igual a 1;
- para valores muito grandes de x, tendendo a infinito (ou muito pequenos, tendendo a menos infinito), a curva tende a zero.
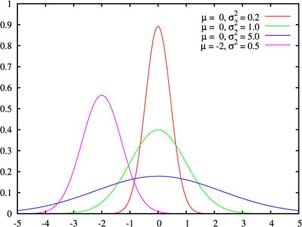
Note que conforme o caso, poderemos ter curvas com formatos diferentes, ou seja, mais para a direita, mais para a esquerda, mais ou menos achatadas... enfim, cada caso poderá gerar uma curva diferente. Vejamos mais um caso.
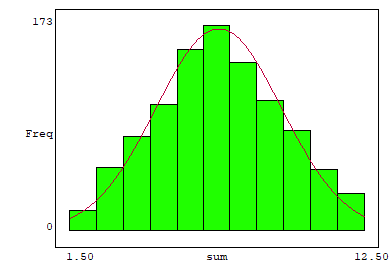
Consideremos o lançamento de dois dados não viciados. Estamos interessados em analisar a soma dos resultados obtidos em cada jogada. Realizando uma simulação e construindo o histograma dos resultados, obtemos:
No caso simulado, obtivemos:
sample mean = 7.07200
sample st dev = 2.34282
Ou seja, μ = 7,07 e s = 2,34, onde μ indica a média (lembre-se que a média amostral é igual à média populacional) e s o desvio padrão da amostra. Isolando a curva da normal temos:
Assim, conforme havíamos dito, existem diferentes curvas, que variam conforme os valores da média e do desvio-padrão.
Lembramos que a área abaixo desse gráfico vale 1. Ou seja, a área corresponde a uma probabilidade.
É aquela região do plano compreendida entre a curva e o eixo das abscissas, que corresponde em qualquer distribuição normal a 100% dos dados considerados.
Consideremos uma população de uma cidade A e de uma outra cidade B. Suponhamos que todas as pessoas tenham informado as respectivas alturas (em centímetros). E deseja-se fazer uma comparação entre tais populações. As principais estatísticas obtidas por essa pesquisa foram:
|
|
População A |
População B |
|
Média (μ) |
174 |
178 |
|
Variância (σ²) |
64 |
1 |
Um pesquisador deseja sortear aleatoriamente pessoas para fazer um teste sobre DNA e crescimento e, para isso, gostaria de coletar (aleatoriamente!) pessoas com mais de 1,80m. Em qual das duas populações será mais fácil achar pessoas com tais características?
Para isso, podemos dizer que estamos trabalhando com duas variáveis:
XA: altura de 1 pessoa selecionada ao acaso na população A
XB: altura de 1 pessoa selecionada ao acaso na população B
Nosso objetivo é calcular as seguintes probabilidades:
P(XA > 180) e P(XB > 180).
Mas antes, calculemos o valor do desvio-padrão (σ) de cada uma das populações. Lembrando que o desvio-padrão nada mais é do que a raiz quadrada da variância. Logo:
Utilizando um software é possível calcularmos tais probabilidades. Esse software calcula, na verdade, a área abaixo da curva:
P(XA > 180) = 0,2266 ou 22,66%.
P(XB > 180) = 0,0228 ou 2,28%.
Portanto, o pesquisador terá mais facilidade de achar pessoas com mais de 1,80m na população A. Aleatoriamente falando, tal probabilidade é de 22,66%.
Esse resultado pode parecer estranho, visto que a população B possui uma média de alturas superior ao da população A. Porém, tal fato é explicado através da variabilidade dos resultados, ou melhor, pelo desvio padrão.
Consideremos, ainda, o exemplo anterior. Só que, agora, temos interesse em obter pessoas que tenham entre 1,75m e 1,80m. Qual população possui um número maior de habitantes nessa faixa de altura?
Aqui, queremos calcular as seguintes probabilidades:
P(175 < XA < 180) e
P(175 < XB < 180) .
Novamente, usando um software, obtemos:
P(175 < XA < 180) = 0,2236 e
P(175 < XB < 180) = 0,9759.
Portanto, é evidente que a população B, mais uma vez, representa a melhor escolha, pois a probabilidade de escolhermos uma pessoa nessa faixa de altura na população B é quase 100%, ou seja, quase todos habitantes possuem as alturas procuradas.
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
Ok! Mas e se eu não tiver um computador? Como calcular as probabilidades da distribuição Normal?
A resposta é simples: USE A TABELA DA DISTRIBUIÇÃO NORMAL PADRÃO!
Em muitos livros de Estatística podemos encontrar uma tabela da Normal Padrão. É uma tabela que nos fornece valores das áreas (= probabilidades) de acordo com o valor de x, exatamente como fizemos nos exemplos anteriores com o auxílio do software Winstats.
A maioria dos softwares de Estatística possuem comandos que permitem calcularmos o valor das áreas sob curvas como a Normal, dentre eles, o SAS, o Excel, o S-PLUS, e outros. Porém, se não temos acesso a um computador, podemos usar a Tabela da Normal. Mas, como dissemos anteriormente, existem diversas curvas da normal, que variam segundo a média e variância. Isso significa que teríamos que ter inúmeras tabelas da normal... o que não parece muito viável.
Dessa forma, criou-se uma maneira mais simples de se obter as áreas desejadas. Criou-se uma curva denominada Normal Padrão, que corresponde a uma distribuição normal com média zero e desvio padrão um. Geralmente a variável aleatória associada à distribuição normal padrão é chamada de Z. Em notação:
Z ~ N(0,1), ou seja, μ Z = 0 e σ Z = 1
A grande vantagem de usarmos tal distribuição é o fato de trabalharmos apenas com uma distribuição e, portanto, com uma única tabela. Tudo é mais fácil!
Porém, como fazer para obtermos tal variável Z (padronizada) a partir de uma variável aleatória qualquer X tal que X ~ N(μ , σ²) ?
Basta padronizarmos ou normalizarmos a variável X através da fórmula:
onde:
μ = média de X
σ = desvio-padrão de X
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
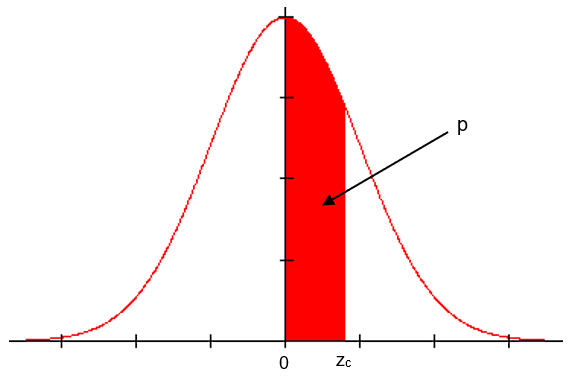
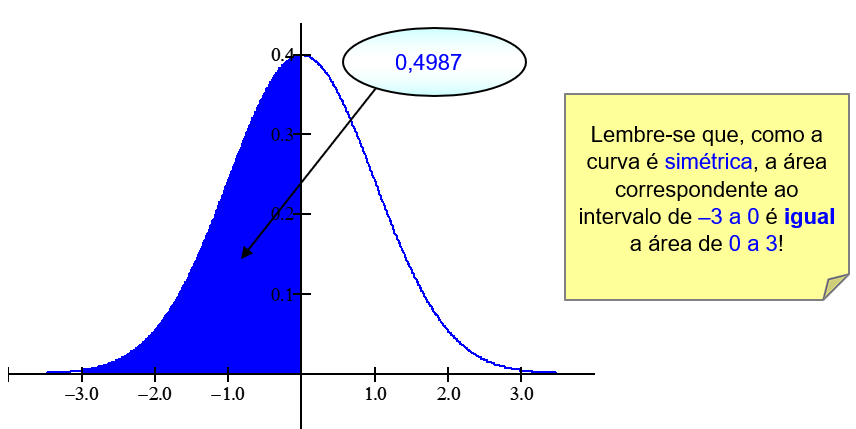
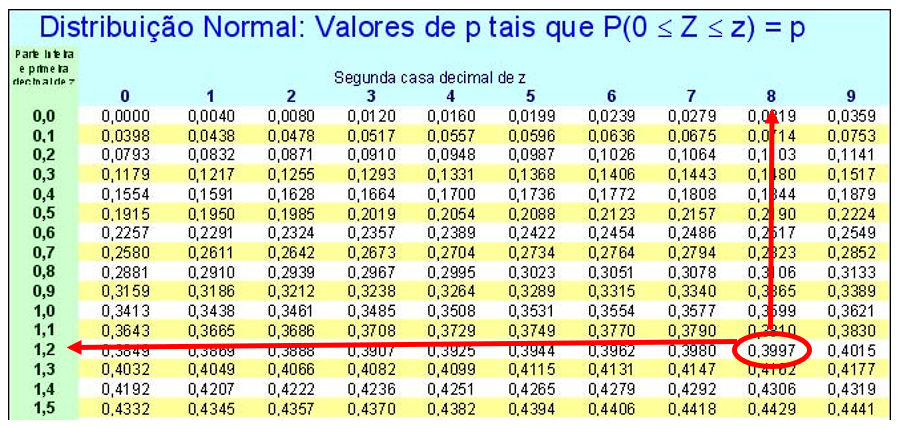
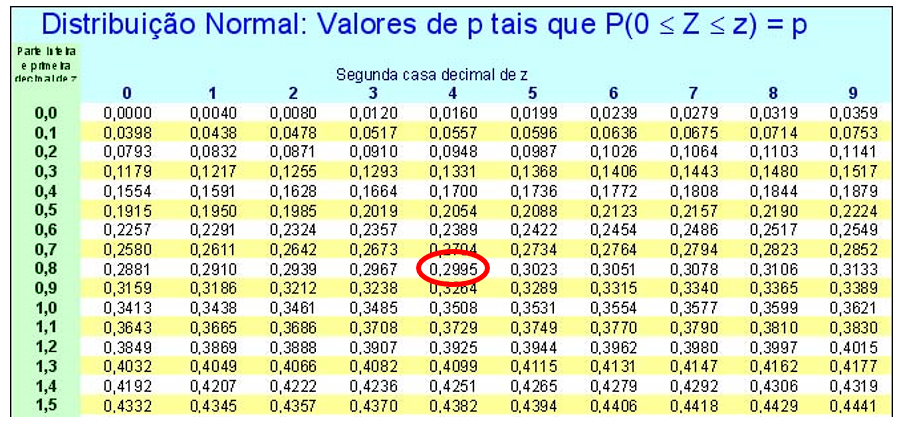
Existem algumas variações de apresentação da tabela. No nosso caso, utilizaremos uma tabela tal que P(0 ≤ Z ≤ zc) = p, ou seja, a probabilidade fornecida pela tabela (p) corresponde ao intervalo que vai de 0 até um certo número z c no eixo x. Esquematicamente, a tabela da normal nos fornece a probabilidade correspondente à área a seguir:
Veja, esquematicamente, como deve ser a leitura da tabela:
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
Voltemos ao caso do exemplo anterior onde tínhamos μ = 174 e σ = 8. Queríamos calcular P(X > 180). Vamos normalizar a variável X (ou seja, transformá-la em Z) e utilizar a tabela para obter a probabilidade desejada.
Para obtermos a probabilidade desejada, devemos lembrar que a nossa tabela nos fornece a probabilidade de 0 até um certo valor.
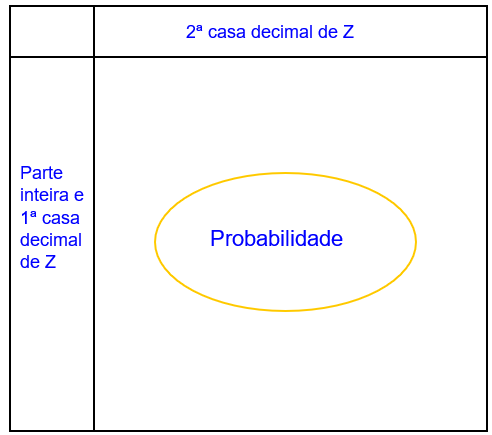
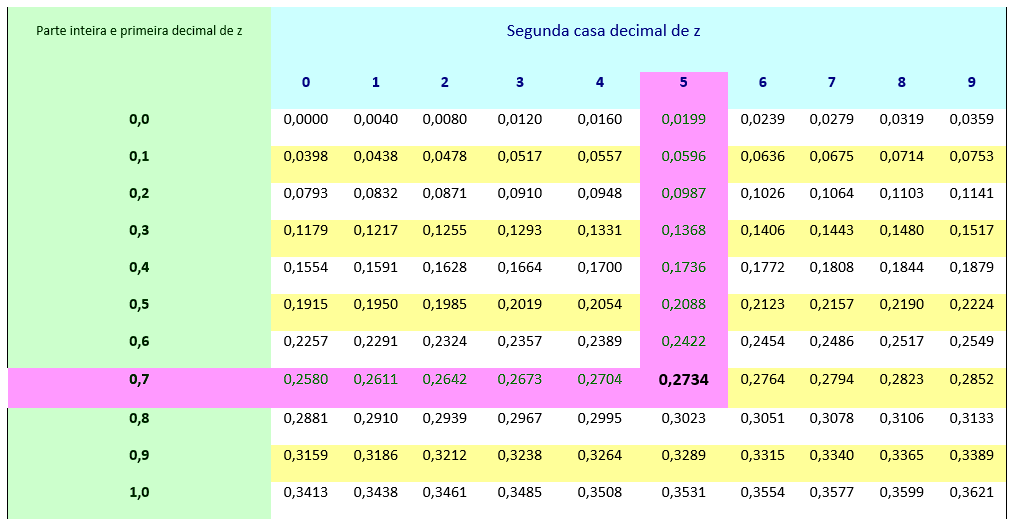
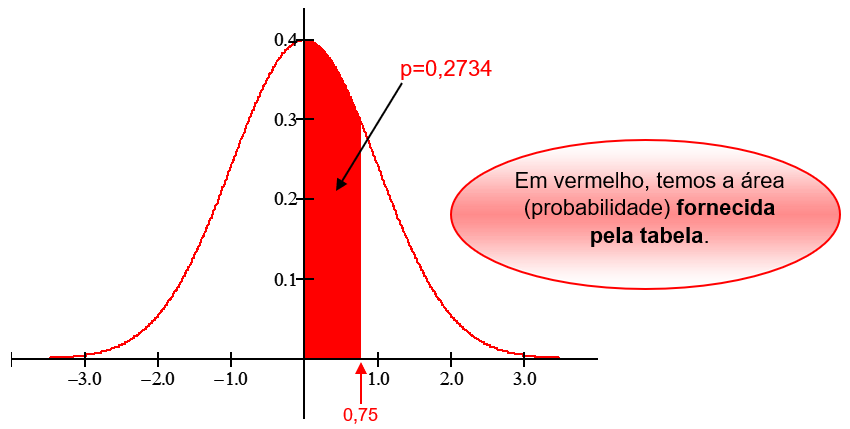
Dado Z = 0,75, vejamos como obter a probabilidade a partir da tabela da Normal Padrão. Na coluna mais à esquerda, tomamos a parte inteira e a primeira decimal de Z, no caso, 0,7. Na linha superior, observamos o valor da segunda casa decimal, no caso 5 (lembre-se que o número é 0,7 5 ). A célula correspondente à linha do número 0,7 e da coluna de 5 é o valor da probabilidade. No caso, p=0,2734.
Então:
Como fazer para calcular o valor desejado a partir do valor da tabela?
Bem, é preciso relembrar as propriedades da curva da normal, em especial duas delas:
1) a área abaixo da curva é igual a 1;
2) a curva é simétrica em torno da média (no caso da normal padrão, em torno do zero).
Logo, concluímos, que a área correspondente à metade da curva é igual a 0,5:
Então, podemos observar que:
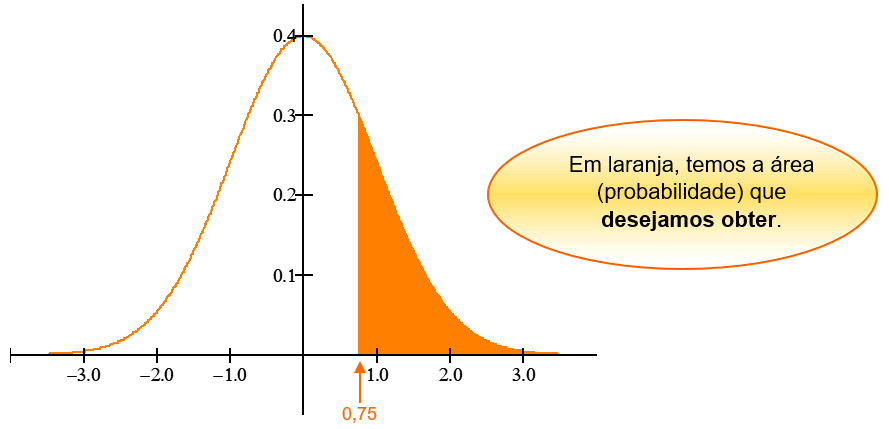
P(0 ≤ Z ≤ 0,75) + P(Z > 0,75) = 0,5
P(Z > 0,75) = 0,5 – P(0 ≤ Z ≤ 0,75)
P(Z > 0,75) = 0,5 – 0,2734
P(Z > 0,75) = 0,2266
Logo, a probabilidade procurada é de 0,2266 que corresponde ao mesmo valor obtido utilizando-se o software (exemplos anteriores).
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
Consideremos a mesma situação das alturas, ou seja, μ = 178, σ = 1 e queríamos calcular a probabilidade P(175 < X < 180).
Normalizando (ou padronizando) a variável X temos:
Graficamente:
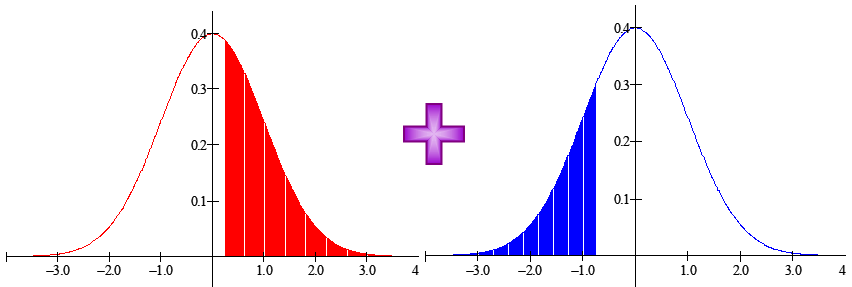
Porém, a nossa tabela só nos fornece os valores:
Clique no botão abaixo para abrir a tabela da Normal Padrão em uma nova janela.
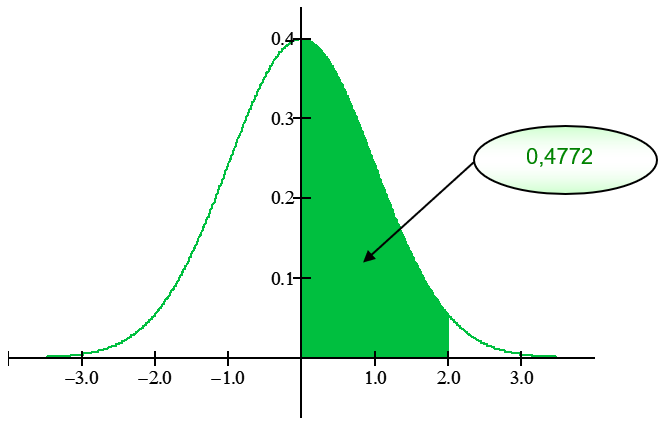
Ver tabela da normal padrãoLogo, a área procurada corresponde à soma das áreas parciais:
P(–3 < Z < 2) = 0,4772 + 0,4987 = 0,9759,
que é igual à probabilidade obtida através do software (exemplos anteriores).
Assim, mostramos que a tabela pode ser muito útil, principalmente quando não temos um computador ou software adequado por perto.
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
Em um certo teste de aptidão para contratação de determinada empresa, os candidatos devem realizar uma sequência de tarefas no menor tempo possível. Suponhamos que o tempo necessário para completar esse teste tenha uma distribuição Normal com média 45 minutos e desvio-padrão de 20 minutos. Suponhamos que, numa primeira etapa, esse teste foi aplicado com uma amostra de 50 candidatos. Qual a probabilidade de encontrarmos algum candidato que tenha um tempo superior a 50 minutos (candidato muito lento) ou inferior a 30 minutos (que seria impossível completar o teste)? Qual o número aproximado de candidatos com tal perfil?
Inicialmente, seja X uma variável que indique o tempo de execução das tarefas tal que X ~ N(45, 20²). Desejamos calcular:
P(X > 50) + P(X < 35) =
= (0,5 – 0,0987) + (0,5 – 0,2734) =
= 0,6279 ou 62,79%
Como 0,6279 . 50 = 31,39, temos que o número de pessoas aproximado que contenham tais característica é de 32 pessoas. Então, nesse teste a empresa já exclui 32 candidatos, restando apenas 18 para continuarem no processo de seleção.
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
1ª) A variável aleatória X pode assumir todo e qualquer valor real.
2ª) A representação gráfica da distribuição normal é uma curva em forma de sino, simétrica em torno da média, que recebe o nome de curva normal ou de Gauss.
3ª) A área total limitada pela curva e pelo eixo das abscissas é igual a 1, já que essa área corresponde à probabilidade de a variável aleatória X assumir qualquer valor real.
4ª) A curva normal é assintótica em relação ao eixo das abscissas, isto é, aproxima-se indefinidamente do eixo das abscissas sem, contudo, alcançá-lo.
5ª) Como a curva é simétrica em torno da média, a probabilidade de ocorrer valor maior que a média é igual à probabilidade de ocorrer valor menor do que a média, isto é, ambas as probabilidades são iguais a 0,5 ou 50%. Cada metade da curva representa 50% de probabilidade.
6ª) Uma variável Normal X com média μ e desvio padrão σ pode ser transformada em uma variável Normal Padrão Z pela fórmula
Qual a probabilidade de escolher-se de forma aleatória, numa só tentativa, uma pessoa que tenha renda anual entre US$ 4.000 e US$ 7.000, morador de uma cidade. Sendo a renda média desta cidade US$ 5.000 e o desvio padrão de US$ 1.500? Sabe–se que a renda populacional possui uma distribuição Normal.
Resolução
Sendo X: renda anual de uma pessoa em dólares, temos:
Consultado a tabela da normal, verificamos que a probabilidade entre z=0 e z=1,33 vale 0,4082. A probabilidade entre z=0 e z=–0,67 é igual, devido à simetria da curva, à probabilidade entre z=0 e z=0,67 e vale 0,2486. Logo:
P(–0,67<Z<1,33) = 0,2486 + 0,4082 = 0,6568 ou 65,68%.
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
Os pesos de 600 estudantes são normalmente distribuídos com média 65,3 kg e desvio padrão 5,5 kg. Determine o número de estudantes que pesam:
a) entre 70 kg e 80 kg
b) mais que 63,2 kg
c) mais que 72 kg
Resolução
Seja X: peso de um estudante em kg.
Logo, haverá 0,1939 . 600 = 116,34 ~ 116 estudantes pesando entre 70kg e 80kg.
Portanto, espera–se encontrar 0,6480 . 600 = 388,8 ~ 389 estudantes com peso superior a 63,2kg.
Assim, devemos encontrar 0,1112 . 600 = 66,72 ~ 67 estudantes com mais de 72kg.
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
Sendo Z uma variável Normal Padrão, calcule as seguintes probabilidades:
a) P (0 < Z < 1,44)
b) P (–1,48< Z < 2,05)
c) P (Z > –2,03)
d) P (Z > 2,03)
e) P (0,72 < Z < 1,89)
f) P (0,72 ≤ Z < 1,89)
g) P (0,72 < Z ≤ 1,89)
h) P (0,72 ≤ Z ≤ 1,89)
i) P(Z = 0,72)
j) P(Z = 1,89)
k) P(Z>4,5)
l) P(Z<4,5)
Resolução
Observe que a variável já está padronizada. Logo, basta consultarmos a tabela para efetuar os cálculos. Sugestão: para compreender melhor, sempre faça um esboço da área procurada.
a) P (0 < Z < 1,44) = 0,4251
b) P (–1,48< Z < 2,05) = 0,4306 + 0,4798 = 0,9104
c) P (Z > –2,03) = 0,5 + 0,4788 = 0,9788
d) P (Z > 2,03) = 0,5 – 0,4788 = 0,0212
e) P (0,72 < Z < 1,89) = 0,4706 – 0,2642 = 0,2064
Para os itens seguintes, perceba que há apenas a alteração entre os símbolos < e ≤. Pensando que a probabilidade corresponde a área sob a curva e que a área sob um único ponto é uma linha e, portanto, tem área igual a zero, concluímos que a adição ou remoção de um ponto não interfere no resultado final. Ou seja:
f) P (0,72 ≤ Z < 1,89) = 0,2064
g) P (0,72 < Z ≤ 1,89) = 0,2064
h) P (0,72 ≤ Z ≤ 1,89) = 0,2064
A área sob um ponto é uma linha, ou seja, a área é igual a zero:
i) P(Z = 0,72) = 0
j) P(Z = 1,89) = 0
Note que a tabela não possui valores de probabilidade para z muito grande (geralmente acima de 4, dependendo da tabela utilizada). Ao mesmo tempo, note que para os últimos valores da tabela, a probabilidade se aproxima de 0,5. Então:
k) P(Z>4,5) = 0,5 – 0,5 = 0
l) P(Z<4,5) = 0,5 + 0,5 = 1
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
Se X é uma variável aleatória tal que X~N(20; 49), Calcule P(X<30).
Resolução
Pela notação da distribuição Normal, X possui média 20 e variância 49. Logo, o desvio padrão vale 7. Assim:
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
O salário semanal dos operários de construção civil de certo país é distribuído normalmente em torno da média de $ 80, com desvio padrão de $5.
a) Qual é o valor do salário para escolhermos 10% dos operários com maiores remunerações?
b) Qual é o maior salário correspondente aos 20% dos trabalhadores que ganham menos?
Resolução
Este exemplo é o contrário dos anteriores. Antes, conhecíamos o valor da variável X, padronizávamos para a variável Z e, usando a tabela da Normal Padrão, obtínhamos o valor da probabilidade procurada. Aqui, vamos fazer exatamente o mesmo caminho só que ao contrário.
a) Queremos calcular um salário a de modo que:
P(X>a) = 0,10.
Padronizando:
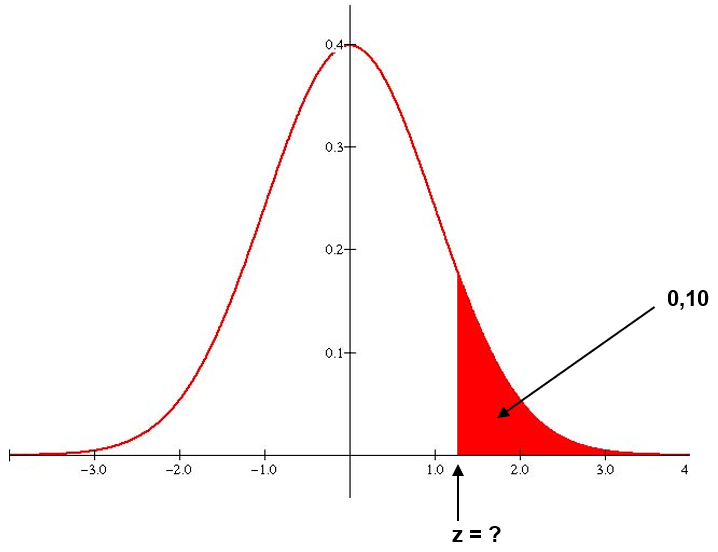
Ou seja, nosso interesse é procurar um valor de z na tabela de modo que a área da curva a seguir seja 0,10.
Consequentemente, vamos procurar na tabela o valor que mais se aproxima de 0,40 (veja a figura seguinte):
Observando a tabela, encontramos o valor de z mais próximo à probabilidade 0,40:
Ou seja, o valor de z desejado é z=1,28. Isso significa que P(Z>1,28) = 0,10. Comparando com a expressão obtida
temos a seguinte igualdade:
Portanto, a=86,4. Conclusão: existem 10% dos operários que ganham acima de $86,40. Esse é, portanto, o salário procurado.
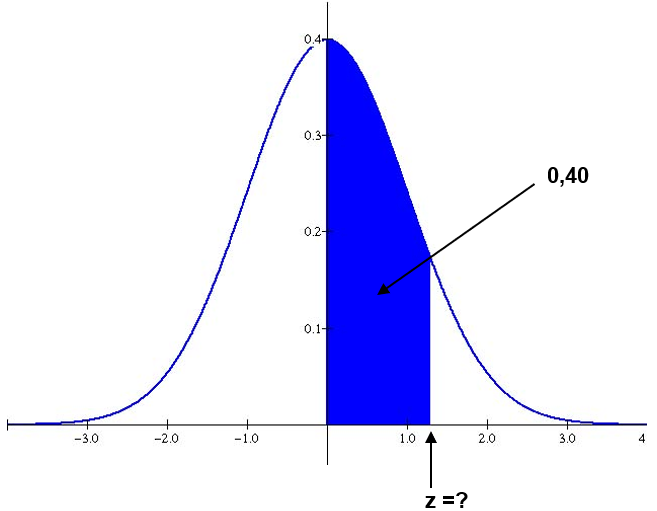
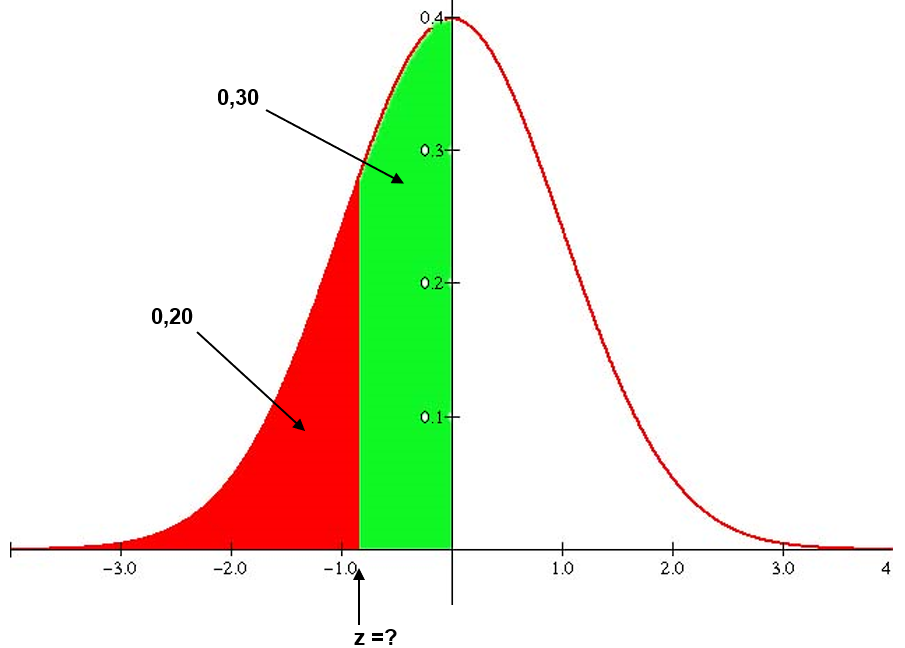
b) Agora, desejamos saber o salário b que separa os 20% que ganham menos dos demais, ou seja:
P(X<b)=0,20
Graficamente, queremos achar, na tabela da Normal Padrão, o valor de z que satisfaz ao gráfico:
Observando a tabela da Normal Padrão, devemos procurar a probabilidade mais próxima de 0,30:
Ou seja, o valor procurado é z=0,84. Porém, olhando o último gráfico, devemos ficar atento para o fato de que o valor que desejamos está à esquerda do zero, ou seja, é um valor negativo. Devido à simetria da curva da Normal, concluímos que o valor de z que realmente queremos é z=–0,84. Em outras palavras, temos que P(Z<–0,84) = 0,20. Logo:
e, portanto, b=75,8.
Assim, o salário semanal de $ 75,80 separa os 20% dos operários que recebem menos.
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
Clique no botão abaixo para abrir a tabela da Normal Padrão em uma nova janela.
Ver tabela da normal padrãoEm uma escola, as notas de um exame são normalmente distribuídas com média de 72 pontos e desvio padrão de 9. O professor atribuirá conceito A aos 8% dos melhores alunos. Qual a menor nota (valor inteiro) que um aluno pode tirar de modo a garantir um conceito A?
Resolução
Seja k a nota procurada e seja X a variável que representa a nota de um aluno. Queremos:
P(X>k)=0,08
Buscando na tabela da normal o valor de z que mais se aproxima da probabilidade igual a 0,5–0,08=0,42, encontramos z=1,41. Ou seja, P(Z>1,41)=0,08. Logo:
Ou seja, a menor nota que o aluno deve tirar para garantir um conceito A é 85.
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
1) O tempo necessário em uma oficina para o conserto da transmissão de um tipo de carro segue distribuição normal com média de 45 minutos e desvio-padrão de 8 minutos. O mecânico comunicou a um cliente que o carro estará pronto em 50 minutos. Qual probabilidade de o mecânico atrasar o seu serviço?
2) A duração de certo componente eletrônico pode ser considerada normalmente distribuída com média de 850 dias e desvio padrão de 45 dias. Calcular a probabilidade de um componente durar:
a) Entre 700 e 1000 dias.
b) Mais de 800 dias.
c) Menos de 750 dias.
3) Determinado atacadista efetua suas vendas por telefone. Após alguns meses, verificou-se que os pedidos se distribuem normalmente com média de 3.000 pedidos e desvio-padrão de 180 pedidos. Qual a probabilidade de que um mês selecionado ao acaso esta empresa venda menos de 2700 pedidos?
4) O conteúdo líquido das garrafas de 300 ml de um refrigerante é normalmente distribuído com média de 300 ml e desvio padrão de 2 ml. Determine a probabilidade de uma garrafa selecionada ao acaso apresentar conteúdo líquido:
a) inferior a 306 ml;
b) superior a 305 ml;
c) entre 302 e 304 ml.
5) O lucro mensal obtido com ações de determinada empresa tem distribuição normal com média de 12 mil reais e desvio padrão de 5 mil reais. Qual a probabilidade de que em determinado mês o lucro desta empresa seja:
a) superior a 18 mil reais;
b) inferior a 8 mil reais;
c) entre 10 e 15 mil reais.
6) Durante o mês de dezembro aumenta a procura por concessão de crédito para pessoa física. De acordo com dados históricos é possível verificar que a procura segue uma distribuição aproximadamente normal com média de 12,8 milhões e desvio padrão de 15 milhões. Se as instituições de crédito reservarem 25 milhões para concessão de crédito, qual a probabilidade de faltar dinheiro para emprestar?
7) Suponha que a renda média anual de uma grande comunidade tenha distribuição normal com média de 15 mil reais e com um desvio-padrão de 3 mil reais. Qual a probabilidade de que um indivíduo aleatoriamente selecionado deste grupo apresente uma média salarial anual superior a 18 mil reais?
8) O escore de um estudante no vestibular é uma variável com distribuição normal com média de 550 pontos e desvio padrão de 30 pontos. Se a admissão em certa faculdade exige um escore mínimo de 575 pontos, qual é a probabilidade de um aluno ser admitido nesta faculdade?
9) As vendas de determinado produto têm apresentado distribuição normal com média de 600 unidades e desvio padrão de 40 unidades. Se a empresa decide fabricar 700 unidades naquele mesmo mês, qual é a probabilidade de ela não poder atender a todos os pedidos desse mês por estar com o estoque esgotado?
10) O volume de enchimento de uma máquina automática usada para encher latas de bebidas gasosas é distribuído normalmente com uma média de 12,4 onças e um desvio padrão de 0,1 onça. Qual a probabilidade do volume de enchimento ser:
a) inferior a 12 onças;
b) entre 12,1 e 12,6 onças;
c) superior a 12,3 onças.
11) O tempo de reação de um motorista para o estímulo visual é normalmente distribuído com uma média de 0,4 segundos com um desvio-padrão de 0,05 segundos. Qual a probabilidade de que uma reação de um motorista requeira:
a) mais de 0,5 segundos;
b) entre 0,4 e 0,5 segundos.
12) O período de falta de trabalho em um mês por causa de doenças dos empregados é normalmente distribuído com uma média de 100 horas e desvio padrão de 20 horas. Qual a probabilidade desse período no próximo mês estar:
a) entre 50 e 80 horas;
b) superior a 90 horas;
c) inferior a 60 horas.
13) X é N(10; 100). Calcular P (12 < X ≤ 20).
14) X é N(30; 16). Calcular P (X < 19).
15) X é N(20; 25). Calcular P (X ≤ 30).
16) X é N(50; 81). Calcular P (40 ≤ X < 60).
17) X é N(10; 16). Calcular P (X ≥ 5).
18) Uma pesquisa indica que as pessoas usam seus computadores por uma média de 2,4 anos antes de trocá–los por uma máquina nova. O desvio padrão é 0,5 anos. Um dono de computador é selecionado de forma aleatória. Encontre a probabilidade de que ele vá usar o computador por menos de 2 anos antes de trocá–lo. Considere uma distribuição normal de probabilidades.
19) Uma pesquisa indica que para cada ida ao supermercado, uma pessoa gasta uma média de 45 minutos, com desvio padrão de 12 minutos naquela loja. Esse tempo gasto na loja é normalmente distribuído. Uma pessoa entra na loja.
a) Qual a probabilidade de que essa pessoa fique na loja entre 24 e 54 minutos?
b) Qual a probabilidade de que essa pessoa fique na loja mais que 39 minutos?
c) Se 200 pessoas entrarem na loja, quantas devem permanecer nela entre 24 e 54 minutos?
d) Se 200 pessoas entrarem na loja, quantas devem permanecer nela por mais de 39 minutos?
20) As pontuações para um teste de serviço civil são normalmente distribuídas com uma média de 75 pontos e um desvio padrão de 6,5. Para ser adequado ao emprego de serviço civil, você deve ter pontuação dentro dos 5% primeiros colocados. Qual é a menor pontuação que você pode obter e ainda assim ser adequado ao emprego? Considere que a pontuação é um valor inteiro.
21) Em uma amostra escolhida aleatoriamente de homens com idade entre 35 e 44 anos, a média do nível de colesterol total era de 210 mg/dl. Suponha que os níveis totais de colesterol sejam normalmente distribuídos com desvio padrão igual a 38,6 mg/dl. Encontre o nível total de colesterol mais alto que um homem nessa faixa etária pode ter dentre os 1% dos homens com menores níveis de colesterol.
22) Você vende uma marca de pneus de automóveis que tem uma expectativa de vida que é normalmente distribuída com uma vida média de 30.000 milhas e um desvio padrão de 2.500 milhas. Você quer dar uma garantia de troca de pneus grátis que não durem muito. Como você poderia honrar sua garantia se você está disposto a trocar 10% dos pneus que vende?
23) Uma máquina de venda automática, distribui café em um copo de 8 decilitros. A quantidade de café no copo é normalmente distribuída com desvio padrão de 0,03. Você pode deixar o café transbordar 1% das vezes. Qual quantidade você deveria marcar como a quantidade média de café a ser distribuído?
24) Os pesos do conteúdo de uma caixa de cereais são normalmente distribuídos com um peso médio de 20 onças e um desvio padrão de 0,07 onça. Caixas nos 5% mais baixos não atendem às condições mínimas de peso e devem ser embaladas novamente. Qual é o peso mínimo exigido para uma caixa de cereais?
1) 0,2643
2) a) 0,9992 b) 0,8665 c) 0,0132
3) 0,0475
4) a) 0,9987 b) 0,0062 c) 0,1359
5) a) 0,1151 b) 0,2119 c) 0,3811
6) 0,2090
7) 0,1587
8) 0,2033
9) 0,0062
10) a) 0 b) 0,9759 c) 0,8413
11) a) 0,0228 b) 0,4772
12) a) 0,1525 b) 0,6915 c) 0,0228
13) 26,2%
14) 0,3%
15) 97,72%
16) 73,3%
17) 89,44%
18) 21,19%
19) a) 0,7333 b) 0,6915 c) 147 pessoas d) 138 pessoas
20) 86 pontos
21) 120 mg/dl
22) Pneus que gastam antes de completarem 26.800 milhas.
23) 7,93 decilitros.
24) 19,88 onças
Faça o download gratuito da apostila sobre Distribuição Normal de Probabilidades em formato PDF.
Baixe AgoraVocê também pode se interessar por:
Intervalos de confiança para a média, proporção, variância e desvio padrão. Como usar a tabela t-Student e a tabela Qui-Quadrado.
Formulação da hipótese nula e da hipótese alternativa, nível de significância, nível descritivo e passo-a-passo para realizar um teste de hipóteses
Teste de hipóteses para a média e para a proporção quando temos apenas uma população. Fórmulas, resolução passo-a-passo e lista de exercícios.