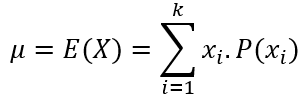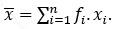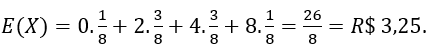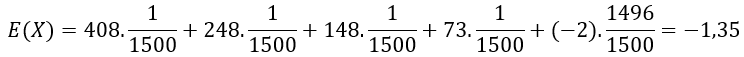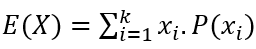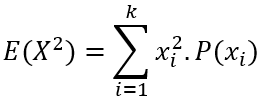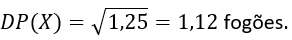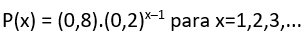1. Introdução

As distribuições de frequências de amostras foram tratadas anteriormente. Agora, trataremos das distribuições de probabilidades de populações. A distribuição de frequência de uma amostra é uma estimativa da distribuição de probabilidade da população correspondente. Se o tamanho da amostra for grande, espera-se que a distribuição de frequências da amostra tenha uma boa aproximação da distribuição de probabilidade da população.

No estudo de pesquisas empíricas e análises de situações reais, a Estatística Descritiva (tabelas de frequências, média, moda, mediana, desvio padrão, etc.) são bastante úteis. Porém, no estudo de uma população, as distribuições de probabilidades, como veremos mais adiante, são preferidas, pois possibilitam a construção de modelos matemáticos que nos auxiliam na compreensão dos fenômenos do mundo real.

2. Variáveis aleatórias

Como já vimos no estudo das probabilidades, o conjunto de todos os possíveis resultados de um experimento aleatório é chamado de espaço amostral. Os elementos desse conjunto podem ser numéricos ou não. Por exemplo, o número de filhos de um casal é um exemplo de conjunto numérico. Porém, o grau de escolaridade de um indivíduo é algo não numérico. Dessa forma, em muitas vezes, para podermos trabalhar probabilisticamente com uma variável não numérica, atribuímos valores para cada elemento do espaço amostral.

O resultado de um experimento de probabilidade geralmente é uma contagem ou uma medida. Quando isso ocorre, o resultado é chamado de variável aleatória.

Definição

Uma variável aleatória X representa um valor numérico associado a cada resultado de um experimento de probabilidade. A palavra aleatória indica que os valores assumidos por X são obtidos ao acaso.

Notação

Geralmente, as variáveis aleatórias são representadas por letras maiúsculas (X), enquanto que os valores assumidos por essas variáveis aleatórias são representadas por letras minúsculas (x). Dessa forma, se escrevermos X=x queremos dizer que a variável aleatória X assume um valor numérico igual a x.

As variáveis aleatórias podem ser de dois tipos: discretas ou contínuas.

2.1. Variáveis aleatórias discretas

Uma variável aleatória é discreta se ela assume um número finito de valores ou assume um número infinito de valores numeráveis (contáveis). Podemos dizer que uma variável é discreta quando seus valores puderem ser listados.

Por exemplo: o número de ligações recebidas por dia em um escritório pode ser um valor igual a 0, 1, 2, 3, 4, ... Assim, definimos a variável aleatória X:

X: número de ligações recebidas pelo escritório.

Os valores que essa variável pode assumir são x=0, 1, 2, 3, ... Dessa forma, se escrevermos X=3 estamos dizendo que “o número de ligações recebidas pelo escritório (X) é igual a 3 ligações (x)”.

2.2. Variáveis aleatórias contínuas

Uma variável aleatória é contínua se ela possui um número incontável de possíveis resultados. Ou seja, uma variável é dita contínua quando os valores que ela pode assumir puderem ser representados como um intervalo na reta dos números reais. Neste caso, os valores assumidos por uma variável contínua, não podem ser listados, visto que são infinitos os possíveis valores dessa variável.

Por exemplo: consideremos o tempo de duração de uma ligação recebida em minutos (incluindo frações de minutos). Neste caso, podemos definir uma variável aleatória Y da seguinte forma:

Y: tempo de duração de uma ligação em minutos.

Perceba que os valores de Y podem assumir qualquer valor em um intervalo real. Suponhamos, para facilitar, que o tempo máximo de uma ligação seja de 120 minutos. Neste caso, os valores y pertencem ao intervalo [0, 120].

3. Distribuições de probabilidades discretas

Para cada valor de uma variável aleatória discreta pode-se determinar uma probabilidade correspondente a esse valor. Ao listar cada valor de uma variável aleatória juntamente à sua probabilidade, você estará formando uma distribuição de probabilidade.

Uma distribuição de probabilidades deve satisfazer as seguintes condições:

I. A probabilidade de cada valor da variável é um número de 0 à 1. Ou seja:

     0 ≤ P(X=x) ≤ 1 ou, ainda, 0 ≤ P(x) ≤ 1.

II. A soma de todas as probabilidades é igual a 1:

     ∑ P(X=x i ) = 1 ou, ainda, ∑ P(xi) = 1 

Perceba que podemos trabalhar com dois tipos de notação: P(X=x) ou simplesmente P(x). Por exemplo, a probabilidade de a variável X assumir o valor igual a 3 pode ser escrita como P(X=3) ou apenas P(3).

Exemplo 1

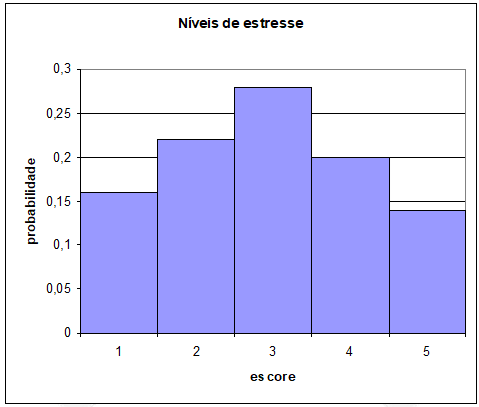
Um psicólogo aplicou um teste para classificar o nível de estresse dos 150 funcionários de uma empresa. Para isso, ele atribuiu cinco possibilidades: muito calmo, calmo, moderado, irritado, muito irritado. Essas características foram pontuadas com valores de 1 à 5, onde 1 indica a qualidade “muito calmo” e 5 indica “muito irritado”. Definindo a variável aleatória X: nível de estresse, podemos dizer que x=1,2,3,4,5. Os resultados da pesquisa estão na tabela a seguir:

Construir uma distribuição de probabilidade para a variável X.

Resolução

Utilizando a tabela, podemos calcular as probabilidades:

P(X=1) = 24/150 = 0,16

P(X=2) = 33/150 = 0,22

P(X=3) = 42/150 = 0,28

P(X=4) = 30/150 = 0,20

P(X=5) = 21/150 = 0,14

A distribuição de probabilidades está apresentada na tabela a seguir:

Graficamente, podemos representar da seguinte forma:

Exemplo 3

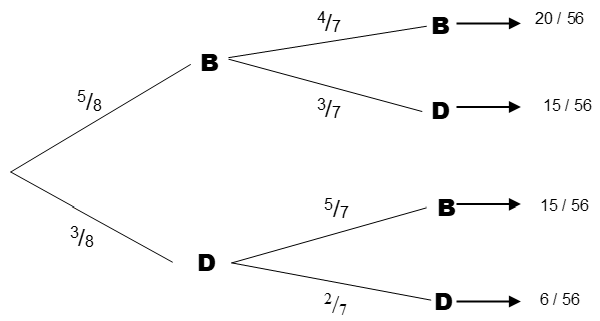
Em uma caixa há 5 peças boas e 3 defeituosas. Duas peças são retiradas ao acaso e sem reposição. Definindo a variável aleatória X como sendo o número de peças boas retiradas, obtenha a distribuição de probabilidades.

Resolução

Vamos construir a árvore de probabilidades:

Definindo:

X: número de peças boas retiradas.

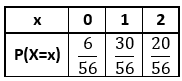
Note que X poderá assumir valores iguais a 0, 1, ou 2. Logo, a distribuição de probabilidades será dada pela tabela:

4. Valor Esperado ou Média de uma variável aleatória discreta

Seja X uma variável aleatória discreta, com valores x1, x2, ..., xk. O valor esperado de X (ou esperança matemática de X), ou simplesmente a média de X é definida através da fórmula:

Já vimos que a média amostral é dada por

A média teórica (ou populacional) μ é semelhante à média amostral. À medida que o tamanho da amostra aumenta, a freqüência relativa fi aproxima-se de p(xi), ou seja, a média amostral aproxima-se da média populacional.

Exemplo 4

Considere um jogo no qual se lançam três moedas não viciadas e se recebe R$ 2,00 caso apareça 1 cara, R$ 4,00 se aparecerem 2 caras e R$ 8,00 caso apareçam 3 caras. Se nenhuma cara ocorrer, nada se recebe. Quanto se esperaria ganhar caso fizesse esse jogo uma vez? Em outras palavras: qual é o valor esperado de uma jogada?

Resolução

Inicialmente, fazendo o estudo das probabilidades (como a construção de uma árvore de probabilidades, por exemplo), verificamos que a probabilidade de ocorrer um certo número de caras é dada pela tabela:

Se definirmos a variável aleatória X: valor a ser recebido, podemos construir a distribuição de probabilidades de X, conforme tabela a seguir:

A esperança (ou valor esperado) será:

O valor esperado é uma média a longo prazo. No caso, após várias jogadas, se esperaria ganhar R$ 3,25.

Exemplo 5

Em um sorteio, 1500 bilhetes são vendidos a R$ 2,00 cada. Serão 4 prêmios sorteados nos valores de R$ 500, R$ 250, R$ 150 e R$ 75. Você compra um bilhete. Qual o valor esperado do seu lucro?

Resolução

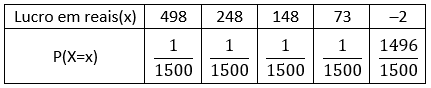
Para encontrar o lucro para cada prêmio, devemos subtrair o valor do prêmio do valor pago pelo bilhete. Assim, para o prêmio de R$ 500, temos um lucro igual a R$ 500 – R$ 2 = R$ 498. E assim por diante para os demais prêmios. Definindo a variável aleatória discreta X: lucro em reais, construímos a distribuição de probabilidades:

Agora, calculamos o valor esperado:

Logo, como o valor esperado é negativo, você espera perder uma média de  R$1,35 por cada bilhete que comprar.

O desvio padrão da variável X corresponde à raiz quadrada da variância:

Exemplo 6

Uma loja possui a seguinte distribuição de vendas de geladeiras por semana:

Calcular o valor esperado de X: número de vendas por semana e o desvio padrão de X.

Resolução

Utilizando a fórmula para a esperança:

E(X) = 0.0,20 + 1.0 ,30 + 2.0,30 + 3.0,15 + 4.0,05 = 1,55 geladeiras.

Vamos calcular a variância. Para isto, precisamos determinar, antes, o valor de E(X²):

E(X2) = 0² .0,20 + 1² .0,30 + 2² .0,30 + 3² .0,15 + 4² .0,05 = 3,65.

Utilizando a fórmula da variância:

Var(X) = E(X²) - E²(X) = 3,65 - (1,55)² = 1,25

O desvio padrão será:

a) Calcular P(x) para x=1, x=2, x=3, x=4 e x=5.

b) Some as probabilidades obtidas no item a. O que você pode dizer a respeito das probabilidades para valores de x maiores que 5?

6) O número de chamadas telefônicas recebidas por uma central e suas respectivas probabilidades para um intervalo de um minuto são:

a) Determinar P(1 ≤ X ≤ 4) e P(X > 1).

b) Qual é o número esperado de chamadas em um minuto?

c) Lembrando que o coeficiente de variação é o quociente entre o desvio padrão e a média, calcule o coeficiente de variação de X.

7) De acordo com uma pesquisa do Data Journal, 70% das pessoas que trabalham em escritórios utilizam computadores da IBM. Se dois indivíduos que trabalham em escritórios são selecionados ao acaso, encontrar a distribuição de probabilidades da variável X: número de usuários dos computadores da IBM. Calcule a média e o desvio padrão dessa variável.

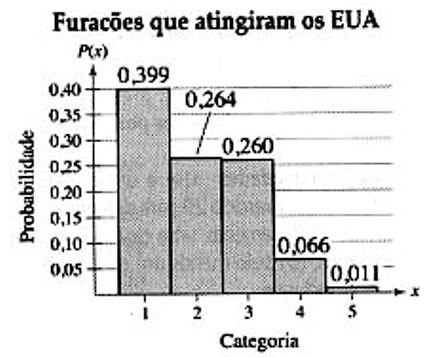
8) O gráfico mostra a distribuição de furacões que atingiram o território dos EUA divididos por categorias, sendo 1 o nível mais fraco e 5 o mais forte.

Para essa variável, calcule:

a) a esperança;

b) a variância;

c) o desvio padrão.

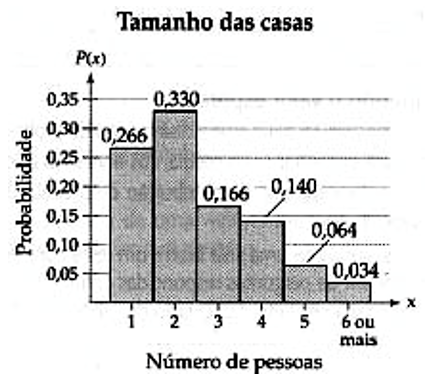
9) O gráfico mostra a distribuição de probabilidades do número de pessoas que moram em cada casa nos EUA:

Respostas dos Exercícios

1) a) 

b) 8/9

c) 5/12

d) 5/18

2) a) K = 105/176      b) 7/22

3)

4) a) 0,15    b) 2,85    c) 1,7275 e 1,31

5) a)

b) A soma das probabilidades é 0,99968. logo, as probabilidades para valores maiores que 5 são próximas de zero.

6) a) 0,43 e 0,20    b) 0,83    d) CV = 145,8%

7)

μ(X) = 1,40

σ(X) = 0,65

8) a) 2,0   b) 1,0   c) 1,0

9) a) 2,5   b) 1,9   c) 1,4

10) $ 0,05