Conrad Elber Pinheiro
Professor Guru
Atualizado em 30/07/2023
Sobre esta página
1. Introdução
2. Hipótese Estatística
3. Teste de Hipóteses
4. Formulação da Hipótese Nula (H₀) e da Hipótese Alternativa (Hₐ)
5. Tipos de Erro e Nível de Significância
6. Nível descritivo ou P–valor
7. Passo–a–passo de um teste de hipóteses
Links importantes sobre Testes de Hipóteses
Ao final desta página, você pode fazer o download gratuito da apostila sobre Testes de Hipóteses em formato PDF.
Clique aqui para assistir a playlist com os conteúdos desta página no YouTube
Neste capítulo, apresentaremos outro método para fazer inferências sobre parâmetros populacionais. Em vez de calcular uma estimativa do parâmetro pontual ou por intervalo, iremos admitir um valor hipotético para um parâmetro populacional, e com base nas informações da amostra realizaremos um teste estatístico, para aceitar ou rejeitar o valor hipotético. Como a decisão para aceitar ou rejeitar a hipótese será tomada de acordo com elementos de uma amostra, fica evidente que a decisão estará sujeita a erros. Estaremos tomando decisões em condições de incerteza e, portanto, sujeitas a erro. Com base nos resultados obtidos em uma amostra, não é possível tomar decisões que sejam definitivamente corretas. Entretanto, como veremos adiante, podemos dimensionar a probabilidade (risco) da decisão de aceitar, ou rejeitar uma hipótese estatística.
Trata-se de uma suposição quanto ao valor de um parâmetro populacional, ou quanto à natureza da distribuição de probabilidade de uma variável populacional.
São exemplos de hipóteses estatísticas:
– a altura média da população brasileira é de 1,65m;
– a proporção de paulistas com certa doença é de 40%;
– homens e mulheres realizam certa tarefa num mesmo intervalo de tempo.
É uma regra de decisão para aceitar ou rejeitar uma hipótese estatística com base nos elementos amostrais.
Para testar um parâmetro populacional, devemos afirmar, cuidadosamente, um par de hipóteses: uma que represente a afirmação e outra que represente o seu complemento. Quando uma dessas hipóteses for falsa, a outra deve ser verdadeira. Essas duas hipóteses são chamadas de hipótese nula e hipótese alternativa.
A Hipótese Nula (H₀) é uma hipótese estatística que contém uma afirmação de igualdade, tal como ≤, = ou ≥.
A Hipótese Alternativa (Hₐ) é, geralmente, o complemento da Hipótese Nula. É a afirmação que deve ser verdadeira se H0 for falsa e contém uma afirmação de desigualdade estrita, tal como <, ≠ ou >.
Por exemplo, se o valor da afirmação for k e o parâmetro populacional for μ, as possíveis hipóteses (nula e alternativa) a serem formuladas são sempre um dos 5 casos a seguir:
H₀: μ = k
Hₐ: μ ≠ k
H₀: μ = k
Hₐ: μ > k
H₀: μ = k
Hₐ: μ < k
H₀: μ ≤ k
Hₐ: μ > k
H₀: μ ≥ k
Hₐ: μ < k
Em muitas situações, de acordo com os dados do problema, podemos formular as hipóteses da forma I ou II, ambas corretas; ou, ainda, I ou III, também ambas corretas. Porém, em situações críticas, é possível que obtenhamos conclusões diferentes se optarmos por uma ou por outra formulação.
Dizemos que o caso I corresponde a um teste bilateral ou bicaudal. Os casos II, III, IV e V correspondem a testes unilaterais ou unicaudais.
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
Em um teste de hipóteses, sempre partimos do pressuposto que a hipótese nula (H0) é verdadeira. Daí, podemos tomar uma destas decisões:
1) Aceitar H₀, rejeitando Hₐ ou
2) Rejeitar H₀, aceitando Hₐ.
Pelo fato de a decisão ser baseada em uma amostra ao invés de ser baseada na população, há sempre a possibilidade de tomarmos a decisão errada.
Por exemplo, suponha que você afirme que certa moeda seja tendenciosa. Para testar sua afirmação, você joga a moeda 100 vezes e obtém 49 caras e 51 coroas. Você provavelmente concordaria que não há evidência para apoiar sua afirmação. Mesmo assim, é possível que a moeda seja tendenciosa e você tenha um resultado incomum.
Mas, e se você joga a moeda 100 vezes e obtém 21 caras e 79 coroas? Seria uma ocorrência rara obter somente 21 caras de 100 jogadas com uma moeda imparcial. Então, você tem provavelmente evidências suficientes para apoiar sua afirmação de que a moeda é tendenciosa. Entretanto, você não pode ter 100% de certeza. É possível que a moeda seja imparcial e que você tenha obtido um resultado incomum.
Se p representa a proporção de caras, a afirmação "a moeda é tendenciosa" pode ser escrita como a afirmação matemática p ≠ 0,5. O complemento "a moeda é imparcial" é escrita como p = 0,5. Então, nossas hipóteses nula e alternativa são:
H₀: p = 0,5
Hₐ: p ≠ 0,5 (afirmação)
Lembre-se, a única maneira de ter certeza absoluta se H₀ é verdadeira ou falsa é testar a população inteira. Pelo fato de sua decisão — rejeitar H₀ ou falhar em rejeitar H₀ (aceitar Hₐ) — ser baseada em uma amostra, você deve aceitar que sua decisão pode estar errada. Você pode rejeitar a hipótese nula quando ela é, na verdade, verdadeira. Ou, você pode falhar em rejeitar a hipótese nula (aceitando Hₐ) quando ela é, na verdade, falsa.
Há dois possíveis tipos de erros, quando realizamos um teste estatístico para aceitar ou rejeitar H₀. Podemos rejeitar a hipótese H₀ , quando ela é verdadeira, ou aceitar H₀, quando ela é falsa.
O erro de rejeitar H₀ , sendo H₀ verdadeira, é denominado Erro tipo I, e a probabilidade de se cometer o Erro tipo I é designada α ("alfa").
O erro de aceitar H₀ , sendo H₀ falsa, é denominado Erro tipo II, e a probabilidade de cometer o Erro tipo II é designada β ("beta").
Os possíveis erros e acertos de uma decisão com base em um teste de hipótese estatístico estão sintetizados no quadro a seguir:
Observe: o Erro tipo I só poderá ser cometido quando se rejeitar H₀ , enquanto o Erro tipo II poderá ocorrer quando se aceitar H₀ .
O tomador de decisão deseja, obviamente, reduzir ao mínimo as probabilidades dos dois tipos de erros. A redução simultânea dos erros poderá ser alcançada pelo aumento do tamanho da amostra, evidentemente, com aumento dos custos. Para um mesmo tamanho de amostra, a probabilidade de incorrer em um Erro tipo II aumenta à medida que diminui a probabilidade do Erro tipo I, e vice-versa.
O nível de significância de um teste é definido como sendo a probabilidade máxima permissível para cometer um Erro tipo I. Ou seja, o nível de significância é igual ao valor α.
A probabilidade de um Erro tipo II é o valor β. O valor 1–β é chamado de poder do teste. Ele representa a probabilidade de rejeitar a hipóteses nula quando a hipótese alternativa for verdadeira. O valor do poder é difícil (e às vezes impossível) de se encontrar na maioria dos casos.
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
Ao realizarmos um teste de hipóteses, partimos de um dado valor de α, pré-fixado, para construir a regra de decisão. Uma alternativa é deixar a cargo de quem vai utilizar as conclusões do teste a escolha do valor para a probabilidade α, que não precisará ser fixado à priori. A idéia consiste em calcular, supondo que a hipótese nula seja verdadeira, a probabilidade de se obter estimativas mais desfavoráveis ou extremas (à luz da hipótese alternativa) do que a que está sendo fornecida pela amostra. Esta probabilidade será o nível descritivo, denotado por P–valor (ou p-value , em inglês). Valores pequenos do P–valor evidenciam que a hipótese nula é falsa pois, sendo a amostra nossa ferramenta de inferência sobre a população, ela fornece uma estimativa que teria probabilidade muito pequena de acontecer, se H₀ fosse verdadeira. O conceito do que é "pequeno" fica a cargo do usuário, que assim decide qual a usar para comparar com o valor obtido do P–valor.
Quanto menor o P–valor do teste, mais evidência há para se rejeitar a hipótese nula. Um P–valor muito pequeno indica um evento incomum. Lembre–se, entretanto, que mesmo um P–valor muito baixo não constitui prova de que a hipótese nula é falsa, somente que esta é provavelmente falsa.
Para usar o P–valor na decisão de um teste de hipóteses, basta compararmos o P–valor com α:
1) Se P–valor ≤ α, então rejeitamos H₀.
2) Se P–valor > α, então aceitamos H₀.
Embora este seja um método para decidirmos sobre qual hipótese devemos aceitar, não trabalharemos com ele aqui. Usar o P–valor é muito comum quando estamos lidando com um software que nos fornece, nos resultados, o P–valor. Trabalharemos com um outro método, que se baseia em regiões críticas de decisão, conforme veremos mais adiante.
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
A seguir, vamos dar uma “receita” que você deverá utilizar para a construção de todos os testes de hipóteses que estudaremos. Sempre siga estes 7 passos para realizar um teste de hipóteses:
Escreva a hipótese nula (H₀) e a hipótese alternativa (Hₐ). Lembre–se que, para H₀ você deve utilizar um destes símbolos: ≤, = ou ≥. Para Hₐ, use <, ≠ ou >.
Calcule o valor observado (zobs, tobs,...) utilizando a fórmula correspondente ao caso que está analisando.
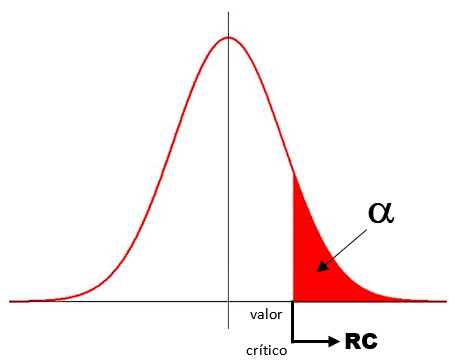
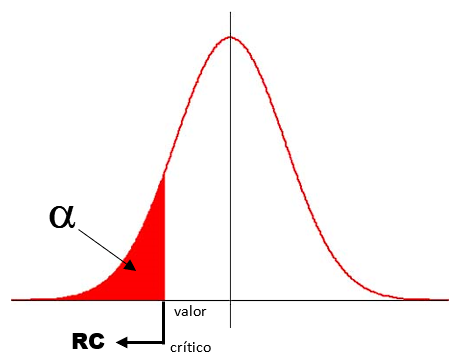
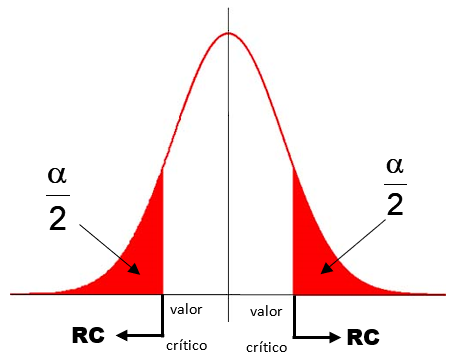
Faça um gráfico da distribuição amostral (Normal, por exemplo). De acordo com a hipótese alternativa (Hₐ), marque a região crítica (RC) do teste:
- Teste Unilateral à direita: Hₐ possui o símbolo >
- Teste Unilateral à direita: Hₐ possui o símbolo <
- Teste Unilateral à direita: Hₐ possui o símbolo ≠
Obtenha o valor crítico do teste (z c , t c ,...) de acordo com o nível de significância do teste (α) e com a região crítica (RC) utilizando a tabela da distribuição correspondente (Normal, t-Student,...). Marque esse valor no gráfico.
Marque o valor observado (zobs, tobs,...) no gráfico.
Conclua o teste:
– se o valor observado pertence à RC , então rejeite H₀ (aceite Hₐ);
– se o valor observado não pertence à RC , então aceite H₀ (rejeite Hₐ).
Interprete, em palavras, a conclusão feita.
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
Faça o download gratuito da apostila sobre Testes de Hipótestes em formato PDF.
Baixe AgoraVocê também pode se interessar por:
Conceitos e propriedades da distribuição Normal, padronização, distribuição Normal Padrão, tabela da Normal Padrão, exemplos resolvidos e lista de exercícios
Intervalos de confiança para a média, proporção, variância e desvio padrão. Como usar a tabela t-Student e a tabela Qui-Quadrado.
Fórmulas e cálculos da média, moda e mediana e lista de exercícios