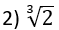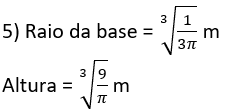Exercício 1

Determine o número real positivo cuja diferença entre ele e seu quadrado seja máxima.

Exercício 2

Determine o número real positivo cuja soma com o inverso de seu quadrado seja mínima.

Exercício 3

A Cia. X Ltda. produz determinado produto e vende-o a um preço unitário de RS 13. Estima-se que o custo total c para produzir e vender q unidades é dado por c = q³ — 3q² + 4q + 2. Supondo que toda a produção seja absorvida pelo mercado consumidor, qual é a quantidade que deve­rá ser produzida para se ter lucro máximo?

Exercício 4

A Cia. Y Ltda. produz um determinado produto e vende-o com um lucro total dado por L(q) = –q³ + 12q² + 60q – 4, onde q representa a quantidade produzida. Determine o lucro máximo e a produção que maximiza o lucro.

Exercício 5

Deseja-se construir uma caixa, de forma cilíndrica, de 1 m³ de volume. Nas laterais e no fundo será utilizado material que custa RS 10 o metro quadrado e na tampa material de R$ 20 o metro quadrado. Determine as dimensões da caixa que minimizem o custo do mate­rial empregado.

Exercício 6

Projetar um jardim retangular de área máxima protegido por uma cerca sabendo que temos 100 m de cerca. Determinar os lados do jardim em metros e a área máxima.

Exercício 7

Deseja-se fazer uma cerca em um terreno retangular  utilizando–se uma parede já existente no terreno. Sabendo que nos temos 200 metros de cerca qual deve ser os tamanhos dos lados do retângulo para que a área obtida seja máxima e qual é a área máxima?

Exercício 8

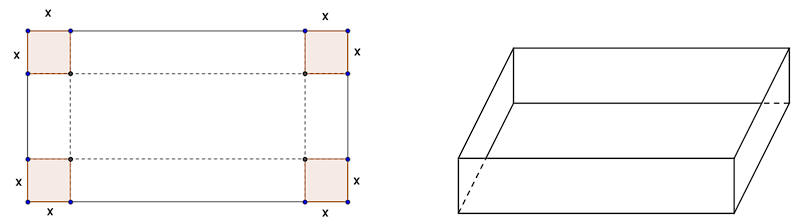
Uma caixa aberta deve ser feita de uma folha de papelão medindo 16 x 30 cm. Qual o tamanho dos quadrados que devem ser cortados nos vértices do retângulo para formar uma caixa de volume máximo?

Exercício 9

Encontrar dois números positivos cuja soma seja 16 e o produto seja o máximo possível. 

Exercício 10

Um jardim retangular de 50 m² de área deve ser protegido contra animais. Se um lado do jardim está protegido por uma parede do celeiro, quais as dimensões desse jardim de modo que a cerca tenha o menor comprimento possível?

Exercício 11

Uma forma líquida de penicilina fabricada por uma firma farmacêutica é vendida a granel a um preço de $200 por unidade. Se o custo total de produção (em dólares) para x unidades for 

C(x) = 500.000 + 80x + 0,003x²

e se a capacidade de produção da firma for de, no máximo, 30.000 unidades em um tempo especificado, quantas unidades de penicilina devem ser fabricadas e vendidas naquele tempo para maximizar o lucro?

Exercício 12

Um certo cartaz deverá ter 600 cm² para a mensagem impressa; deve ter 7,5 cm de margem no topo e na base e uma margem de 5 cm em cada lado. Determine as dimensões totais do cartaz para que a quantidade de papel usada seja mínima. 

Exercício 13

Uma livraria pode receber da editora o livro Estatística Básica a um custo de R$ 40. A gerente da livraria estima que pode vender 180 exemplares a um preço de R$ 100 e que cada redução de R$ 5 no preço fará aumentar 30 cópias nas vendas. Qual deve ser o preço do livro para maximizar o lucro total da livraria?

Exercício 14

Um recipiente com a forma de um paralelepípedo com base quadrada deve ter volume de 2000 cm³. O custo da base e da tampa é de R$ 50/cm² e o custo das laterais é de 30/cm². Encontre as dimensões do recipiente de menor custo possível. 

3) 3 unidades

4) q = 10 e L(10) = 796

6) Os lados terão dimensões 25 m x 25 m.

7) Um lado medirá 100m e dois lados medirão 50m. A área máxima é 5000 m².

8) Os quadrados devem ter lados aproximadamente iguais a 3,33 cm.

9) 8 e 8.

10) 5m (lados perpendiculares à parede) e 10m (lado paralelo à parede).

11) 20000 unidades

12) 45 x 30cm

13) R$ 85,00

14) Base: 10,6 cm de lado; Altura: 17,8 cm.