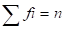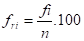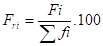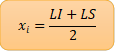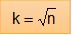Conrad Elber Pinheiro
Professor Guru
Atualizado em 07/07/2023
1. ROL
2. Tabelas
3. Frequências
4. Distribuição de Frequências
5. Classes
6. Limite inferior e limite superior
7. Amplitude de classe e amplitude total
8. Ponto médio de uma classe
9. Escolha do número e tamanho de classes
1°) Classes desiguais: critério subjetivo
2°) Classes de mesmo tamanho; número de classes pré-fixado
3°) Regra de Sturges
4°) Critério da raiz quadrada
5°) Critério da desigualdade: k é o menor inteiro tal que 2^k >= n
10. Alguns problemas na montagem das classes
11. Comparação da Regra de Sturges com outros critérios
12. Lista de Exercícios
Respostas dos Exercícios
Ao final desta página, você pode fazer o download gratuito da apostila sobre Estatística Descritiva e Organização de Dados em formato PDF.
Clique aqui para assistir a playlist com os conteúdos desta página no YouTube
A partir de uma pesquisa, os resultados obtidos, chamados de dados brutos, estão de forma desordenada, geralmente na mesma ordem em que foram obtidos ao longo dessa pesquisa. Para começar a compreender melhor esses dados, é necessário fazer uma organização deles de modo a se conseguir extrair algumas informações para uma análise detalhada posterior a respeito das características de estudo.
A maneira mais elementar para se organizar inicialmente os dados provenientes de uma pesquisa é através da construção de tabelas, como veremos adiante.
Chama-se ROL a sequência dos dados brutos ordenada de forma não decrescente.
Suponhamos uma pesquisa em que 10 casais foram entrevistados com relação ao número de filhos que possuíam. Os resultados obtidos, na ordem das entrevistas (dados brutos) foram: 2, 1, 1, 3, 0, 1, 0, 0, 0, 2.
Para estes dados, podemos construir o ROL: 0, 0, 0, 0, 1, 1, 1, 2, 2, 3.
Importante: note que o ROL possui a mesma quantidade de dados inicialmente coletados. Ou seja, em nosso exemplo anterior, obteve-se 10 valores. Logo, o ROL deve possuir 10 valores também.
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
Consiste em dispor os dados em linhas e colunas distribuídas de modo ordenado. A elaboração de tabelas segue as normas do Instituto Brasileiro de Geografia e Estatística (IBGE).
Os principais elementos de uma tabela são:
- título: descreve que tipos de dados serão apresentados na tabela;
- cabeçalho: contém a descrição de cada coluna da tabela;
- corpo: contém os dados agrupados por linhas;
- rodapé: local onde se pode acrescentar informações complementares da tabela, tais como fonte dos dados, observações e notas.
Quando trabalhamos com dados quantitativos (numéricos), basicamente podemos construir dois tipos de tabelas, de acordo com as variáveis analisadas: tabela para variáveis discretas ou tabela para variáveis contínuas. Quando a variável é contínua, surge, na tabela, um elemento que agrupa tais valores chamado de classe.
Frequências simples ou absolutas (f i ) - é o número de vezes que se observa determinado valor. A soma de todas as frequências absolutas corresponde ao tamanho total da amostra (n):
Frequências relativas (f ri ) – são os valores das razões (quociente) entre as frequências simples e a frequência total multiplicada por 100 para que os dados sejam apresentados em porcentagem:
Frequência Acumulada Simples (F i ) – valores obtidos adicionando a cada frequência absoluta os valores das frequências anteriores. Algumas vezes esta frequência é representada através da notação f ac:
Fk = f1 + f2 + …+fk
Frequência Acumulada Relativa (F ri ) – É a frequência acumulada da classe, dividida pela frequência total da distribuição. Multiplicando-se o resultado por 100 obteremos as frequências em porcentagem. Algumas vezes esta frequência é representada através da notação f acr.
A tabela de dados brutos pode não ser prática para responder às questões de interesse, portanto, a partir da tabela de dados brutos, podemos construir uma nova tabela com as informações resumidas, para cada variável. Essa tabela é denominada de tabela de frequência (ou distribuição de frequência) e, como o nome indica, conterá os valores de variável e suas respectivas contagens.
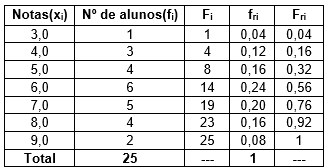
Consideremos o quadro seguinte que mostra as notas de Estatística dos alunos de uma classe.
|
Número |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
21 |
22 |
23 |
24 |
25 |
|
Nota |
5,0 |
4,0 |
6,0 |
8,0 |
3,0 |
5,0 |
7,0 |
6,0 |
8,0 |
4,0 |
6,0 |
9,0 |
7,0 |
5,0 |
7,0 |
5,0 |
6,0 |
8,0 |
7,0 |
9,0 |
4,0 |
6,0 |
6,0 |
8,0 |
7,0 |
Os dados apresentados na tabela acima estão na forma primitiva (dados brutos).
Para facilitar, vamos escrever o ROL desse conjunto de dados:
3, 4, 4, 4, 5, 5, 5, 5, 6, 6, 6, 6, 6, 6, 7, 7, 7, 7, 7, 8, 8, 8, 8, 9, 9.
Agora, mostraremos, passo a passo como construir a tabela de distribuição de frequências.
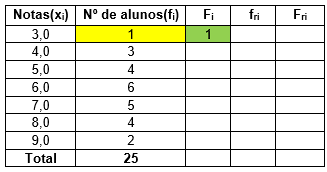
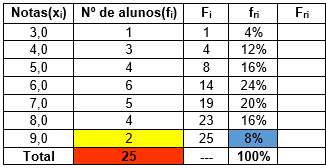
Identificar qual é a nossa variável de estudo (xi). No caso, estamos analisando as notas dos alunos. Então, Notas correspondem aos valores que estamos observando (xi) com uma respectiva frequência absoluta (fi) que corresponde a quantidade de alunos que obteve determinada nota.
Assim, montamos o esqueleto da nossa tabela, sempre lembrando de colocar os totais na última linha.
Verificamos no ROL quais valores foram observados, ou seja, quais as notas que existem no ROL. Marcamos, em ordem crescente, esses valores na coluna dos valores observados (xi):
Vamos completar a coluna das frequências absolutas (fi). A frequência absoluta de um certo valor corresponde a quantas vezes esse valor ocorreu um nosso conjunto de dados. Em nosso exemplo, a frequência absoluta corresponde a quantos alunos tirou determinada nota.
Calculamos o total da coluna fi. Para isso, basta somar todos os valores que aparecem nessa coluna.
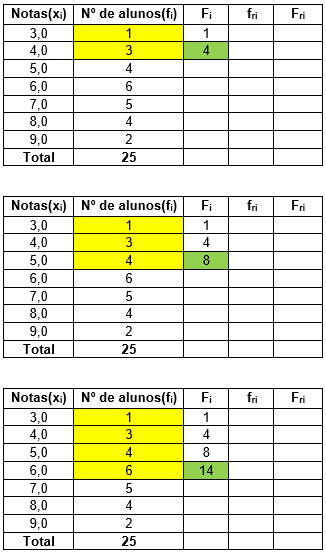
Cálculo da frequência acumulada (Fi).Os valores dessa coluna tem como objetivo “acumular” a soma dos valores das frequências absolutas até a linha em questão. A ideia aqui é formar sempre um L, conforme veremos a seguir: o campo em verde é preenchido com a soma de todos os valores da coluna amarela.
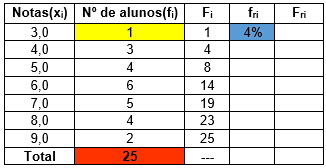
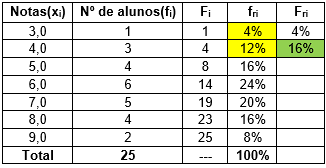
Calcularemos, agora, as frequências relativas absolutas (fri). Para calcular, devemos dividir, para cada linha da tabela, a frequência absoluta (fi) pelo total (n). O resultado da divisão poderá ser multiplicado por 100 de modo a ser apresentado na forma de porcentagem. Nos exemplos a seguir, dividimos a célula indicada em amarelo pelo total da coluna (indicado em vermelho). O resultado foi multiplicado por 100 e colocado na célula azul.
Fazemos, aqui, (1 / 25) x 100 = 4%:
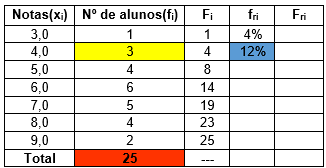
Fazemos, aqui, (3 / 25) x 100 = 12%:
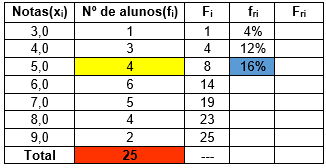
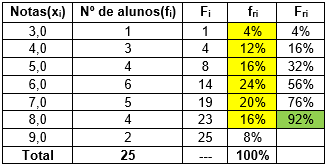
Fazemos, aqui, (4 / 25) x 100 = 16%:
Prosseguimos com o mesmo procedimento até a última linha da tabela. Neste caso, fazemos (2 / 25) x 100 = 8%:
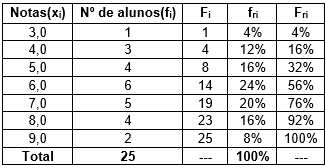
Cálculo da coluna de frequências relativas acumuladas (Fri). Esta coluna pode ser calculada com base na coluna de frequências relativas absolutas (fri), de modo análogo ao que fizemos no 5º PASSO. Veja alguns resultados:
A tabela de frequências completa será:
Uma alternativa à construção da tabela anterior seria a de colocar os valores das frequências relativas absolutas (fri) e acumuladas (Fri) na forma decimal, ou seja, no cálculo, basta não multiplicarmos o resultado da divisão por 100 conforme explicado anteriormente. Nesse caso, todos os valores estariam dentro do intervalo de 0 a 1. Consequentemente, a soma dos valores da coluna fri seria exatamente 1. Nossa tabela ficaria:
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
Quando temos dados brutos provenientes de uma variável contínua, devemos agrupá-los, para a construção de uma tabela, em intervalos que também são conhecidos por classes.
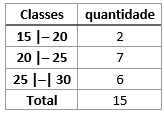
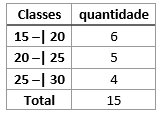
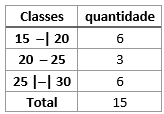
Os tipos de classes ou intervalos estão exemplificados na tabela a seguir:
Consideremos o seguinte ROL:
16, 18, 20, 20, 20, 20, 22, 23, 23, 25, 25, 26, 26, 29, 30.
Vamos construir três tabelas, apenas para compararmos as formas de agrupamento de acordo com a representação utilizada:
Embora as três tabelas estejam corretas, o mais comum é trabalharmos com um padrão, conforme ocorre nas tabelas 1 e 2. Dentre esses dois padrões, o mais comum é o da tabela 1. Note que na última classe da tabela 1, fechamos os dois extremos, visto que o valor 30 pertencia ao nosso conjunto de dados brutos representados no ROL e esse valor corresponde ao maior valor da última classe da tabela. Assim, a última classe ficou com intervalo fechado tanto a esquerda quanto a direita. Isso pode, e deve, ser feito, quando o maior valor do ROL coincidir com o valor representado na última classe evitando que precisemos criar uma nova classe para inserir um único valor.
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
Limite inferior é sempre o valor da esquerda. Vamos abreviar o limite inferior por LI. Considerando as tabelas 1, 2 e 3 anteriores, na primeira classe temos LI=15, na segunda classe, LI=20 e, por fim, na terceira classe temos LI=30.
Limite superior é sempre o valor da direita. Vamos abreviar o limite superior por LS. Considerando as tabelas 1, 2 e 3 anteriores, na primeira classe temos LS=20, na segunda classe, LS=30 e, por fim, na terceira classe temos LS=50.
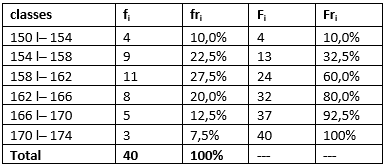
Consideremos a tabela 1 apresentado no exemplo anterior. Perceba que todas as classes possuem o mesmo tamanho. A primeira classe é 15 |─ 20. O limite inferior da primeira classe é 15. O limite superior da primeira classe é 20. A amplitude de classe corresponde à diferença entre o limite superior e inferior. Ou seja: amplitude de classe = 20-15 = 5.
Ainda com relação à tabela 1, vamos observar os extremos da tabela. O mínimo é 15, enquanto que o máximo vale 30. Portanto, a amplitude total da tabela é 30 - 15 = 15.
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
A tabela de distribuição de frequências abaixo representa a altura de 40 jovens. Note que altura é uma variável contínua e, por isso, estamos trabalhando com os dados agrupados em classes:
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
Mais adiante, veremos que precisaremos de um valor conhecido como ponto médio, todas as vezes em que estivermos trabalhando com tabelas contendo classes.
O ponto médio de cada classe é obtido somando os limites superior e inferior da classe e dividindo o resultado por 2.
Em outras palavras, o ponto médio nada mais é do que a média aritmética dos limites superior e inferior da classe em questão.
Geralmente, o ponto médio é representado por xi e, portanto:
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
Spiegel (1975) apresenta algumas sugestões de como elaborar uma distribuição de frequências:
“1. Determinam-se o maior e o menor número dos dados brutos e, então, calcula-se a amplitude total do rol (diferença entre o maior e o menor daqueles números).
2. Divide-se a amplitude total em um número conveniente de intervalos de classe que tenham a mesma amplitude. Se isto não é possível, usam-se intervalos de classe de amplitudes diferentes ou abertos. O número de intervalos de classe é comumente tomado entre 5 e 20, dependendo dos dados. Os intervalos de classe são escolhidos também, de maneira que seus pontos médios coincidam com os dados realmente observados. Isso tende a diminuir o denominado erro de agrupamento que surge em análises matemáticas ulteriores. Entretanto, os limites reais de classe não coincidiriam com os dados realmente observados.
3. Determinam-se o número de observações que caem dentro de cada intervalo de classe, isto é, calculam-se as frequências de classe.”
Vejamos, também, o que Lima (2001) diz a respeito: “apesar de não adotarmos nenhuma regra formal quanto ao total de faixas, utilizamos, em geral, de 5 a 8 faixas com mesma amplitude. Entretanto, ressaltamos que faixas de tamanho desigual podem ser convenientes para representar valores na extremidade da tabela.”
Assim, mais uma vez, notamos que as classes podem ser formadas de acordo com um critério subjetivo, mas não dispensando o bom senso. Em nosso caso, os valores extremos (1,55m e 1,90m) coincidem com valores de fato observados. Nem sempre é necessário que ocorra tal coincidência. Por exemplo, na tabela, nosso valor poderia ser 1,50m, porém, conforme vimos, isso acarretaria em uma perda maior ainda de informações.
Nas duas tabelas que construímos, utilizamos 4 classes. Três delas possuem tamanho 0,10 e apenas uma tem 0,05. Ao contrário do que afirmam alguns autores, os tamanhos das classes não precisam ser iguais e, também, não existe uma regra fixa para se determinar o número de classes.
Daremos a seguir 5 formas de determinarmos a quantidade e o tamanho de cada classe. Para isso, suponhamos uma amostra de tamanho 200 em que observamos as idades das pessoas. A menor idade foi 10 anos e a maior, 70 anos.
As classes variam segundo os interesses do pesquisador. No exemplo, foram construídas 6 classes, de acordo com algumas fases da vida. As classes apresentam tamanhos (amplitudes) diferentes:
Suponhamos que desejamos construir 7 classes. O valor mínimo da nossa amostra é 10 e o máximo é 70. A amplitude total (AT) é:
AT = máx. – mín.
AT = 70 – 10 = 60
Como o número de classes (k) é 7, a amplitude de cada classe (h) é:
h = AT / k
h = 60 / 7 = 8,57
Vamos utilizar h = 9. Utilizamos uma amplitude de classe um pouco superior à calculada. Por isso, a 7ª classe vai de 64 até 73 (embora o maior valor observado seja 70). Obteremos:
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
É uma das regras mais utilizadas na prática. Vamos utilizar a regra de Sturges para calcular o número de classes (k). Se tivermos n valores, o número de classes será:
Essa fórmula pode ser “resumida” na tabela a seguir:
Em nosso caso, n = 200. Logo:
k = 1 + 3,3.log 200
k = 1 + 3,3 . 2,3010
k = 1 + 7,5933
k = 8,5933 que arredondaremos para 9
A amplitude de cada classe é
h = (70 - 10) / 9 = 6,6 que arredondamos para 7.
Finalmente, as classes são:
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
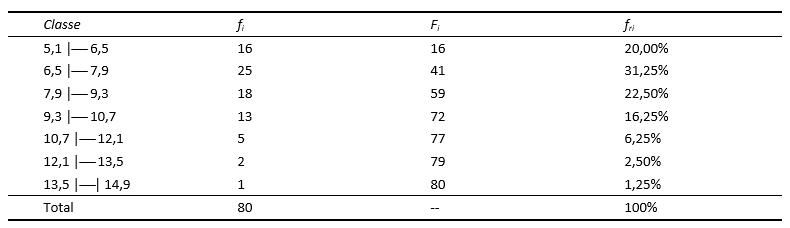
Construir uma tabela com as distribuições de frequências absoluta e acumulada para os 80 valores a seguir, utilizando a Regra de Sturges:
Observando a tabela, temos que:
- Total de dados: n=80.
- Limite inferior (ou valor mínimo): LI = 5,1.
- Limite superior (ou valor máximo): LS = 14,9.
- Amplitude total: AT = LS - LI = 14,9 - 5,1 = 9,8
- Número de classes (fórmula de Sturges):
k = 1 + 3,3 . log n
k = 1 + 3,3 . log 80
k = 7,28
Arredondando, temos: k = 7.
- Amplitude do intervalo de cada classe:
h = 9,8/7 = 1,4
Quando necessário, arredondar o valor de h sempre para mais.
A partir desse resultado, construímos a tabela:
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
O número de classes (k) é dado por
Em nosso exemplo:
O tamanho de cada classe é
Vamos considerar h = 5. Teremos:
(Nota: a última classe teve os dois extremos fechados.)
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
O objetivo deste critério é encontrar o menor número de classes (k) de modo que 2 elevado a esse valor k seja maior ou igual ao tamanho da amostra (n).
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
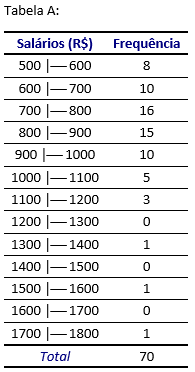
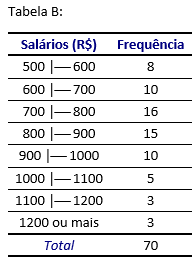
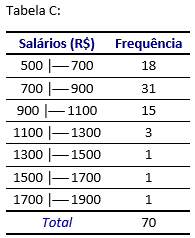
Vejamos alguns exemplos que nos permitam verificar alguns problemas que ocorrem com certa frequência na escolha das classes a serem utilizadas.
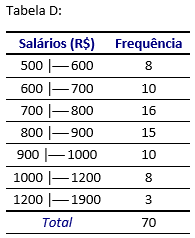
Na tabela A, foi mantida a mesma amplitude de intervalo de classe (R$ 100) em toda a tabela. Como resultado, há muitas classes com frequência igual a zero e os detalhes são “escassos” para salários altos.
Na tabela B, as classes vazias e os detalhes escassos foram evitados mediante emprego do intervalo aberto “1200 ou mais”. A desvantagem disso é que a tabela torna inaplicável a realização de certos cálculos matemáticos.
Na tabela C, foi adotada uma amplitude do intervalo de classe igual a R$ 200. Uma desvantagem é que desaparecem muitas informações referentes aos salários menores e os detalhes ainda são escassos para salários mais altos.
Na tabela D, foram empregadas amplitudes de intervalo de classe desiguais. Uma desvantagem é que certos cálculos matemáticos (quando feitos sem o auxílio de um computador) perdem a simplicidade. Também, quanto maior for a amplitude do intervalo de classe, tanto maior será o erro de agrupamento.
A Regra de Sturges é uma das regras mais utilizadas na Estatística. Isso porque a fórmula de Sturges nos fornece uma quantidade adequada de classes para os mais variados tamanhos de amostras.
Existem várias regras e critérios para a determinação do número de classes. Aqui, estudamos, além da Regra de Sturges, o critério da Raiz Quadrada e o critério da Desigualdade. É importante notar que dependendo do critério adotado e do tamanho da amostra, teremos quantidade de classes diferentes para cada critério. Na tabela a seguir, podemos comparar os resultados para cada um dos três critérios considerando amostras de tamanhos 20, 200, 2000 e 20000:
Perceba que o critério da Raiz Quadrada só é adequado para valores pequenos de n (funciona bem para valores de n menores que 100 ou, no máximo, 150). Já o critério da Desigualdade e a Regra de Sturges, nos fornecem resultados muito próximos. Porém, devido à dificuldade em se calcular o valor de k no critério da Desigualdade, geralmente acabamos por optar em trabalhar com a Regra de Sturges.
Assista a vídeo aula sobre o conteúdo acima no YouTube e baixe os slides da aula em PDF
1) A massa (em quilogramas) de 17 trabalhadores de uma empresa com 100 funcionários está registrada a seguir:
52 73 80 65 50 70 80 65 70 77 82 91 52 68 86 70 80.
Com base nos dados obtidos, responda:
a) Qual a população e a unidade estatística dessa pesquisa?
b) Qual é a sua amostra?
c) Qual é a variável nessa pesquisa? Ela é discreta ou contínua?
d) Que frequências absolutas têm os valores 65 kg, 75 kg, 80 kg e 90 kg?
2) Em uma escola, o conceito de cada bimestre é representado por letras: A, B, C, D e E. Em um determinado bimestre, os conceitos, em Ciências, dos alunos de uma determinada série foram os seguintes:
Nessas condições, elabore um quadro de distribuição de frequências absolutas e frequências absolutas acumuladas.
3) A cantina de uma escola selecionou 50 alunos ao acaso e verificou o número de vezes por semana que eles compravam lanche., obtendo os seguintes resultados: 0; 2; 2; 4; 3; 2; 2; 1; 1; 2; 1; 1; 0; 1; 1 ; 1; 1; 1; 1; 2; 2; 2; 3; 2; 2; 2; 0; 2; 2; 1; 1; 0; 2; 0; 2; 2; 2; 2; 2; 2; 2; 2; 2; 2; 2; 2; 1; 2; 5; 4.
a) Construa uma tabela de distribuição de frequências absolutas e frequências absolutas acumuladas com esses dados.
b) Quantos alunos compram pelo menos 2 lanches por semana?
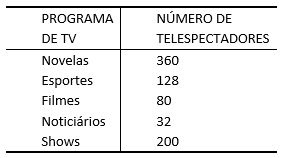
4) Numa pesquisa de opinião pública com 800 telespectadores sobre o programa de televisão de sua preferência, obteve-se a seguinte tabela de frequências absolutas:
Construa uma tabela com distribuição de frequências relativas.
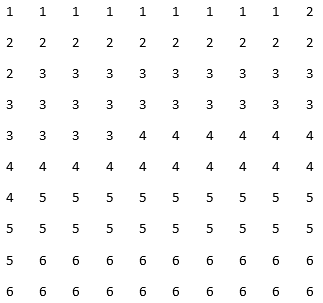
5) Um dado foi jogado 20 vezes. Em cada jogada foram obtidos os seguintes pontos: 1, 5, 6, 5, 2, 2, 2, 4, 6, 5, 2, 3, 3, 1, 6, 6, 5, 5, 4, 2.
a) Elabore um quadro com distribuição de frequências absolutas, frequências absolutas acumuladas, frequências relativas e frequências relativas acumuladas.
b) Quantas vezes o número 3 foi obtido no dado?
c) Quantas vezes o número obtido no dado foi menor que 5?
d) Qual o índice, em porcentagem, em que o número 6 foi obtido no dado?
e) Qual o índice, em porcentagem, em que números maiores que 4 foram obtidos?
6) Veja os principais motivos alegados por 30 000 devedores, pesquisados em uma região metropolitana, ao justificar atrasos do crediário ou cheques sem fundo
Quais as frequências absolutas para cada tipo devedor?
7) A tabela abaixo apresenta as vendas de determinado aparelho elétrico, durante um mês, por uma firma comercial. Apresente os resultados numa distribuição de frequência discreta.
14 12 11 13 14 13
12 14 13 14 11 12
12 14 10 13 15 11
15 13 16 17 14 14
8) Considerando as notas de um teste de inteligência aplicado a 100 alunos, apresentar os resultados numa distribuição de frequência absoluta e relativa. Utilize a regra de Sturges.
9) Os salários de 20 funcionários de uma certa empresa estão listados no rol:
525, 579, 580, 599, 606, 613, 700, 780, 890, 900, 1100, 1150, 1200, 1300, 1300, 1330, 1450,1500, 1500, 1500.
Complete a tabela:
Baseado na tabela, responda:
a) Qual a amplitude total?
b) Qual a amplitude de classe?
c) Qual o limite inferior da segunda classe?
d) Qual o limite superior da terceira classe?
e) Quantos funcionários ganham pelo menos R$ 1100,00?
f) Qual a porcentagem de funcionários que ganha no máximo R$ 900,00?
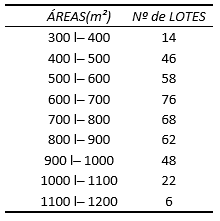
10) A tabela abaixo apresenta uma distribuição de frequência das áreas de 400 lotes:
Com referência a essa tabela, determine:
a) A amplitude total.
b) O limite superior da quinta classe.
c) O limite inferior da oitava classe.
d) O ponto médio da sétima classe (xi).
e) A amplitude do intervalo da segunda classe.
f) A frequência da quarta classe.
g) A frequência relativa da sexta classe.
h) A frequência acumulada da quinta classe.
i) O número de lotes cuja área não atinge 700m².
j) O número de lotes cuja área atinge e ultrapassa 800m².
k) A porcentagem dos lotes cuja área não atinge 600m².
l) A classe do 72º lote.
m) A porcentagem dos lotes cuja área é de 500 m², no mínimo, mas inferior a 1000 m² .
n) A porcentagem dos lotes cuja área seja maior ou igual a 900 m².
11) Complete a tabela de frequência a seguir:
12) Foi realizada uma entrevista com 30 pessoas a respeito do número de irmãos que elas possuíam. Os resultados são apresentados no ROL: 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 2, 3, 3, 3, 3, 4, 4, 4, 5.
a) Construa uma tabela com as frequências absolutas, frequências absolutas acumuladas e frequências relativas.
b) Quantas pessoas possuem pelo menos 2 irmãos?
c) Qual a porcentagem de pessoas que possui no máximo 1 irmão?
d) Quantas pessoas tem menos que 3 irmãos?
13) Os pesos de 40 alunos de uma classe estão descritos abaixo:
69 57 72 54 93 68 72 58 64 62
65 76 60 49 74 59 66 83 70 45
60 81 71 67 63 64 53 73 81 50
67 68 53 75 65 58 80 60 63 53
Pede-se:
a) Dispor os dados em um rol;
b) Construir uma distribuição de frequência do tipo contínua utilizando a fórmula de Sturges. Dado: log 40 = 1,60.
14) No quadro a seguir estão registradas as massas, em quilograma, de 50 pessoas que frequentam uma academia de ginástica. Use a fórmula de Sturges.
15) Conhecidas as notas de 50 alunos, obtenha uma distribuição de frequência com intervalos de classes iguais a 10 considerando o limite inferior da tabela igual a 30.
Determine:
a) a frequência relativa
b) a frequência acumulada
c) a frequência acumulada relativa
d) o intervalo de maior frequência
e) o limite inferior da 5a classe
f) a amplitude total da distribuição
g) quantas classes contém pelo menos 15% das observações?
h) quantos alunos obtiveram nota menor que 50?
i) quanto alunos obtiveram nota maior ou igual a 70?
j) qual a porcentagem de alunos que obtiveram nota maior ou igual a 40 e menor que 60?
k) qual o limite superior da terceira classe?
l) qual o ponto médio da quarta classe?
m) qual a porcentagem de alunos que obtiveram nota inferior a 90?
n) qual a porcentagem de alunos que obteve nota pelo menos igual a 50?
16) Considerando os resultados de 100 lançamentos de um dado, forme uma distribuição de frequência com esses dados e depois responda às questões:
a) qual resultado teve a maior ocorrência?
b) qual a frequência do resultado que teve a menor ocorrência?
c) qual a porcentagem de lançamentos que obtiveram resultados menores que 5?
d) qual a frequência relativa do resultado 6?
e) quantas vezes o número obtido no dado foi maior que 1?
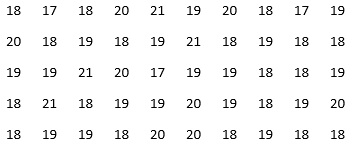
17) Uma pesquisa sobre a idade, em anos de uma classe de calouros de uma faculdade, revelou os seguintes valores:
Determine as frequências absolutas relativas, frequências acumuladas e frequências acumuladas relativas e, em seguida, responda:
a) quantas pessoas possuem idade igual a 17 anos?
b) qual a porcentagem de calouros com 18 anos?
c) qual a porcentagem de pessoas com idade maior ou igual a19 anos?
d) quantos alunos possuem idade entre 18 e 20, incluindo 18 e 20?
18) O Departamento Pessoal de certa firma fez um levantamento dos salários dos 150 funcionários do setor administrativo, obtendo os seguintes resultados:
Com referência a essa tabela, determine:
a) determine as frequências simples relativas, frequências absolutas acumuladas e frequências relativas acumuladas.
b) a frequência da quinta classe.
c) a frequência relativa da oitava classe.
d) a frequência acumulada da sexta classe.
e) o número de funcionários que ganham até 10 salários (exclusive).
f) o número de funcionários que ganham pelo menos 12 salários.
g) a porcentagem dos funcionários que ganham menos de 8 salários.
h) a porcentagem dos funcionários que ganham no mínimo, 4 salários e no máximo, 16 salários (exclusive).
i) o intervalo de maior frequência.
j) a classe do 100º salário.
k) a classe do 142º salário.
l) a classe do 87º salário.
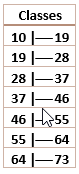
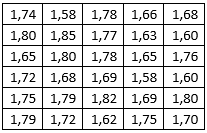
19) Considere as alturas de 30 pessoas, conforme tabela a seguir:
a) construa o rol.
b) determine o limite inferior e o limite superior da distribuição.
c) utilizando a fórmula de Sturges, determine a quantidade de classes para se fazer o agrupamento dos dados.
d) determine a amplitude de cada classe.
e) construa uma tabela de frequências.
f) qual o ponto médio da terceira classe?
g) qual a classe que possui maior frequência?
h) quantas pessoas possuem altura inferior a 1,73?
i) qual o limite superior da quarta classe?
j) qual o limite inferior da quinta classe?
k) a qual classe pertence a 20ª altura?
l) a qual classe pertence a 16º altura?
m) a qual classe pertence a 22º altura?
20) A distribuição abaixo indica o número de acidentes ocorridos com 70 motoristas de uma empresa de ônibus:
Determine:
a) O número de motoristas que não sofreram nenhum acidente.
b) O número de motoristas que sofreram pelo menos 4 acidentes.
c) O número de motoristas que sofreram menos de 3 acidentes.
d) A percentagem de motoristas que sofreram no mínimo 3 e no máximo 5 acidentes.
e) A percentagem de motoristas que sofreram no máximo 2 acidentes.
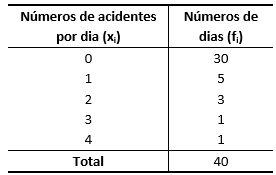
21) Construa a distribuição de frequências para a série abaixo que representa o número de acidentes em determinado cruzamento observados por dia, durante 40 dias.
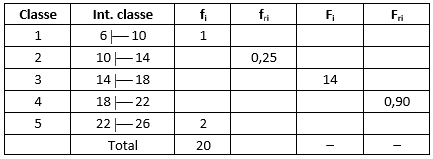
22) Complete o quadro de distribuição de frequências.
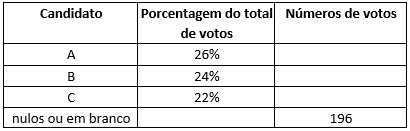
23) (Unifor-CE) Em certa eleição municipal foram obtidos os seguintes resultados:
O número de votos obtido pelo candidato vencedor foi:
a) 178
b) 182
c) 184
d) 188
e) 191
1) a) população: 100 trabalhadores; unidade: trabalhador
b) 17 trabalhadores
c) massa; discreta
d) 2, 0, 3 e 0.
2)
|
Xi |
fi |
Fi |
|
A |
3 |
3 |
|
B |
4 |
7 |
|
C |
8 |
15 |
|
D |
4 |
19 |
|
E |
1 |
20 |
|
total |
20 |
--- |
3) a)
|
xi |
fi |
Fi |
|
0 |
5 |
5 |
|
1 |
13 |
18 |
|
2 |
27 |
45 |
|
3 |
2 |
47 |
|
4 |
2 |
49 |
|
5 |
1 |
50 |
|
total |
50 |
--- |
b) 32
4)
|
programa |
fi |
fri |
|
Novelas |
360 |
45% |
|
Esportes |
128 |
16% |
|
Filmes |
80 |
10% |
|
Noticiários |
32 |
4% |
|
Shows |
200 |
25% |
|
total |
800 |
100% |
5) a)
|
xi |
fi |
Fi |
fri |
Fri |
|
1 |
2 |
2 |
10% |
10% |
|
2 |
5 |
7 |
25% |
35% |
|
3 |
2 |
9 |
10% |
45% |
|
4 |
2 |
11 |
10% |
55% |
|
5 |
5 |
16 |
25% |
80% |
|
6 |
4 |
20 |
20% |
100% |
|
total |
20 |
--- |
100% |
--- |
b) 2
c) 11
d) 20%
e) 45%
6) 5400, 5100, 3600, 3600, 2400, 1500
7)
|
xi |
fi |
Fi |
fri |
Fri |
|
10 |
1 |
1 |
4,2% |
4,2% |
|
11 |
3 |
4 |
12,5% |
16,7% |
|
12 |
4 |
8 |
16,7% |
33,4% |
|
13 |
5 |
13 |
20,8% |
54,2% |
|
14 |
7 |
20 |
29,1% |
83,3% |
|
15 |
2 |
22 |
8,3% |
91,6% |
|
16 |
1 |
23 |
4,2% |
95,8% |
|
17 |
1 |
24 |
4,2% |
100% |
|
total |
24 |
--- |
100% |
--- |
8) AT = 108-62 = 46
k = 1 + 3,3 . log100 = 7,6 ~ 8
h=46 / 8 = 5,75 ~ 6
|
nota |
fi |
Fi |
|
62 |- 68 |
5 |
5 |
|
68 |- 74 |
14 |
19 |
|
74 |- 80 |
16 |
35 |
|
80 |- 86 |
24 |
59 |
|
86 |- 92 |
16 |
75 |
|
92 |- 98 |
13 |
88 |
|
98 |- 104 |
10 |
98 |
|
104 |¾ 110 |
2 |
100 |
|
total |
100 |
--- |
9) a)
|
R$ |
Freq. absoluta |
Freq. acumulada |
Freq. Relativa absoluta |
Ponto médio |
|
500 l─ 700 |
6 |
6 |
30% |
600 |
|
700 l─ 900 |
3 |
9 |
15% |
800 |
|
900 l─ 1100 |
1 |
10 |
5% |
1000 |
|
1100 l─1300 |
3 |
13 |
15% |
1200 |
|
1300 l─| 1500 |
7 |
20 |
35% |
1400 |
|
total |
20 |
--- |
100% |
--- |
b) 1000
c) 200
d) 700
e) 1100
f) 10
g) 45%
10) a) 900 b) 800 c) 1000 d) 950 e) 100 f) 76 g) 15,5% h) 262 i) 194 j) 138 k) 29,5%
l) 3ª classe (500|--600) m) 78% n) 19%
11)
|
i |
Estaturas(cm) |
fi |
xi |
fri |
Fi |
Fri |
|
1 |
150 |- 154 |
4 |
152 |
10,0% |
4 |
10,0% |
|
2 |
154 |- 158 |
9 |
156 |
22,5% |
13 |
32,5% |
|
3 |
158 |- 162 |
11 |
160 |
27,5% |
24 |
60,0% |
|
4 |
162 |- 166 |
8 |
164 |
20,0% |
32 |
80,0% |
|
5 |
166 |- 170 |
5 |
168 |
12,5% |
37 |
92,5% |
|
6 |
170 |- 174 |
3 |
172 |
7,5% |
40 |
100% |
|
|
|
|
----- |
|
------- |
--------- |
12) a)
|
No. De irmãos |
fi |
Fi |
fri |
|
0 |
6 |
6 |
20% |
|
1 |
10 |
16 |
34% |
|
2 |
6 |
22 |
20% |
|
3 |
4 |
26 |
13% |
|
4 |
3 |
29 |
10% |
|
5 |
1 |
30 |
3% |
|
total |
30 |
- |
100% |
b) 14
c) 54%
d) 22pessoas
13) AT=48 k=6,28 ~ 6 h=8
|
pesos |
fi |
Fi |
fri (%) |
Fri (%) |
|
45 |- 53 |
3 |
3 |
7,5 |
7,5 |
|
53 |- 61 |
11 |
14 |
27,5 |
35 |
|
61 |- 69 |
12 |
26 |
30 |
65 |
|
69 |- 77 |
9 |
35 |
22,5 |
87,5 |
|
77 |- 85 |
4 |
39 |
10 |
97,5 |
|
85 |-| 93 |
1 |
40 |
2,5 |
100 |
|
total |
40 |
--- |
100 |
--- |
14)
|
Massas(kg) |
fi |
xi |
fri |
Fi |
Fri |
|
47 |- 55 |
4 |
51 |
8% |
4 |
8% |
|
55 |- 63 |
6 |
59 |
12% |
10 |
20% |
|
63 |- 71 |
9 |
67 |
18% |
19 |
38% |
|
71 |- 79 |
12 |
75 |
24% |
31 |
62% |
|
79 |- 87 |
8 |
83 |
16% |
39 |
78% |
|
87 |- 95 |
9 |
91 |
18% |
48 |
96% |
|
95 |- 103 |
2 |
99 |
4% |
50 |
100% |
|
total |
50 |
- |
100% |
-- |
-- |
15)
|
Notas |
fi |
fri |
Fi |
Fri |
|
30 |- 40 |
4 |
8% |
4 |
8% |
|
40 |- 50 |
6 |
12% |
10 |
20% |
|
50 |- 60 |
9 |
18% |
19 |
38% |
|
60 |- 70 |
11 |
22% |
30 |
60% |
|
70 |- 80 |
9 |
18% |
39 |
78% |
|
80 |- 90 |
7 |
14% |
46 |
92% |
|
90 |- 100 |
4 |
8% |
50 |
100% |
|
Σ |
50 |
100% |
- |
- |
d) 4ª classe (60 |¾ 70)
e) Li = 70
f) AT = 100 – 30 = 70
g) 3
h) 10
i) 20
j) 30%
k) 60
l) 65
m) 92%
n) 80%
16)
|
Faces |
fi |
fri |
Fi |
Fri |
|
1 |
9 |
9% |
9 |
9% |
|
2 |
12 |
12% |
21 |
21% |
|
3 |
23 |
23% |
44 |
44% |
|
4 |
17 |
17% |
61 |
61% |
|
5 |
20 |
20% |
81 |
81% |
|
6 |
19 |
19% |
100 |
100% |
|
Σ |
100 |
100% |
- |
- |
a) 3
b) 9
c) 61%
d) 19%
e) 91
17)
|
Idade (anos) xi |
Nº de alunos (fi) |
fri |
Fi |
Fri |
|
17 |
3 |
6% |
3 |
6% |
|
18 |
18 |
36% |
21 |
42% |
|
19 |
17 |
34% |
38 |
76% |
|
20 |
8 |
16% |
46 |
92% |
|
21 |
4 |
8% |
50 |
100% |
|
Σ |
50 |
100% |
- |
- |
a) 3
b) 36%
c) 58%
d) 43
18)
|
Classe |
Faixa salarial (SM) |
Nº de funcionários |
fri |
Fi |
Fri |
|
1 |
0 |- 2 |
30 |
20% |
30 |
20% |
|
2 |
2 |- 4 |
36 |
24% |
66 |
44% |
|
3 |
4 |- 6 |
21 |
14% |
87 |
58% |
|
4 |
6 |- 8 |
18 |
12% |
105 |
70% |
|
5 |
8 |- 10 |
15 |
10% |
120 |
80% |
|
6 |
10 |- 12 |
12 |
8% |
132 |
88% |
|
7 |
12 |- 14 |
9 |
6% |
141 |
94% |
|
8 |
14 |- 16 |
6 |
4% |
147 |
98% |
|
9 |
16 |- 18 |
3 |
2% |
150 |
100% |
|
|
Σ |
150 |
100% |
- |
- |
b) 15
c) 4%
d) 132
e) 120
f) 18
g) 70%
h) 54%
i) 2º intervalo (2 |¾ 4)
j) 4ª (6 |¾ 8)
k) 8ª (14 |¾ 16)
l) 3ª (4 |¾ 6)
19) a) 1,58 1,58 1,60 1,60 1,62 1,63 1,65 1,65 1,66 1,68 1,68 1,69 1,69 1,70 1,72 1,72 1,74 1,75 1,75 1,76 1,77 1,78 1,78 1,79 1,79 1,80 1,80 1,80 1,82 1,85
b) Li=1,58 Ls=1,85
c) 6
d) 0,05
e)
|
Classe |
Alturas |
fi |
Fi |
|
1 |
1,58 |- 1,63 |
5 |
5 |
|
2 |
1,63 |- 1,68 |
4 |
9 |
|
3 |
1,68 |- 1,73 |
7 |
16 |
|
4 |
1,73 |- 1,78 |
5 |
21 |
|
5 |
1,78 |- 1,83 |
8 |
29 |
|
6 |
1,83 |- 1,85 |
1 |
30 |
|
|
Σ |
30 |
-- |
f) 1,705
g) 5ª (1,78 |- 1,83)
h) 16
i) 1,78
j) 1,78
k) 4ª (1,73 |- 1,78)
l) 3ª (1,68 |- 1,73)
m) 5ª (1,78 |- 1,83)
20) a) 20 b) 15 c) 46 d) 29% e) 66%
21)
|
Nº de acidentes (xi) |
Nº de dias (fi) |
fri |
Fi |
Fri |
|
0 |
30 |
0,75 |
30 |
0,75 |
|
1 |
5 |
0,125 |
35 |
0,875 |
|
2 |
3 |
0,075 |
38 |
0,95 |
|
3 |
1 |
0,025 |
39 |
0,975 |
|
4 |
1 |
0,025 |
40 |
1,000 |
|
Total |
40 |
1,00 |
- |
- |
22)
|
Classe |
Int. classe |
fi |
fri |
Fi |
Fri |
|
1 |
6 |-10 |
1 |
0,05 |
1 |
0,05 |
|
2 |
10 |- 14 |
5 |
0,25 |
6 |
0,30 |
|
3 |
14 |- 18 |
8 |
0,40 |
14 |
0,70 |
|
4 |
18 |- 22 |
4 |
0,20 |
18 |
0,90 |
|
5 |
22 |- 26 |
2 |
0,10 |
20 |
1,00 |
|
– |
Total |
20 |
1,00 |
– |
– |
23) alternativa b
Faça o download gratuito da apostila sobre Estatística Descritiva e Organização de Dados em formato PDF.
Baixe AgoraVocê também pode se interessar por:
Gráficos de linha, coluna, barras, pizza, dispersão, histograma, erros comuns na construção de gráficos, como enganar com gráficos. Clique aqui e saiba mais.
Fórmulas e cálculos da média, moda e mediana e lista de exercícios
Desvio médio, variância populacional, variância amostral, desvio padrão populacional, desvio padrão amostral e coeficiente de variação